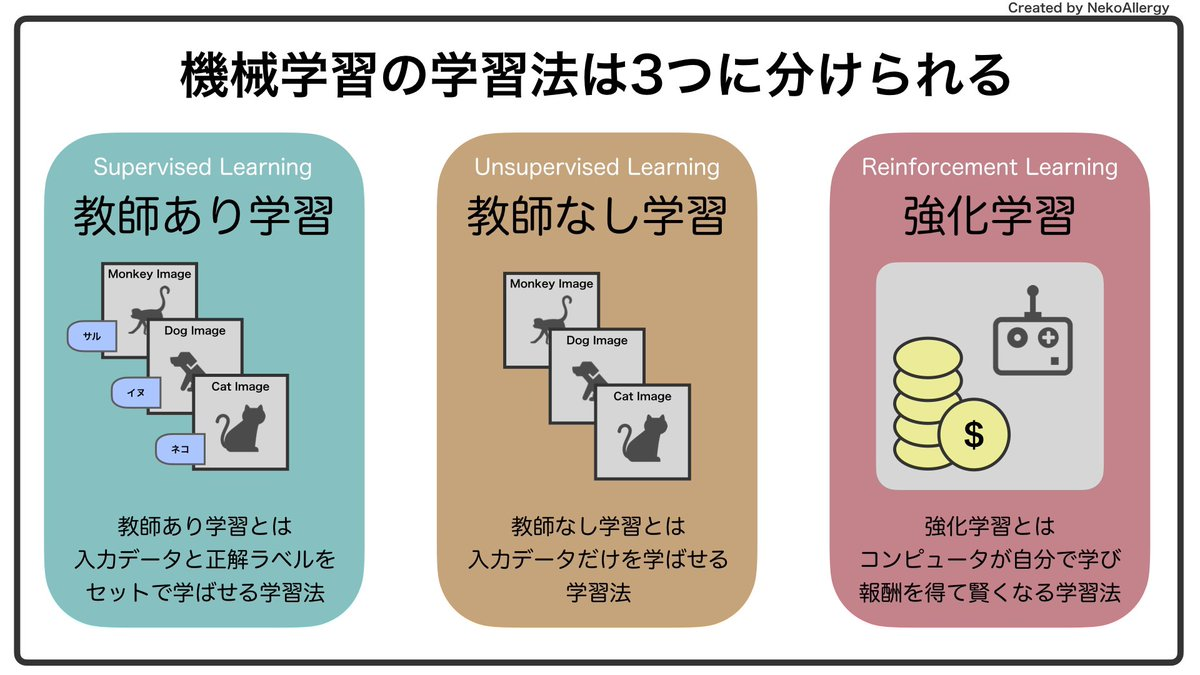
AI, 機械学習, ディープラーニングの違い
機械学習とは
機械学習とは、コンピューターが大量のデータを学習し、分類や予測などのタスクを遂行するアルゴリズムやモデルを自動的に構築する技術。
機械学習の手法は大まかに3種類に分類される。
| 手法 | 代表例 |
|---|---|
| 教師あり学習 | 回帰, 分類 |
| 教師なし学習 | クラスタリング |
| 強化学習 | 囲碁, 将棋 |
回帰:数値を予測する
分類:カテゴリを予測する
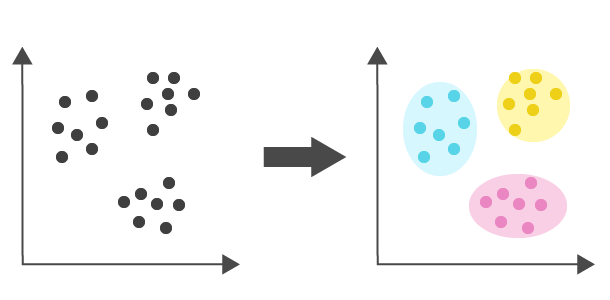
クラスタリング:データをもとに特徴を抽出する
分類とクラスタリングの違い
分類とクラスタリングは別物!!
分かりやすいように大量のメールを分類する例とクラスタリングする例を考える。
・分類
教師あり学習。迷惑メールか否かなど、答えが分かっているデータから文章の特徴とクラスの関係を学習する。そしてクラスが不明の新着メールがどのクラスに当てはまるのかを予測する。
・クラスタリング
教師なし学習。迷惑メールか否かなどの答えがないデータから文章の特徴を学習し、特徴が似ているか否かでグループ分けをする。各グループが何を示しているかは解釈が必要。

分類にも二種類ある
出力層の性質上、ニューラルネットワークの分類問題はクラス数により下記の2つに大別される。
・二値分類(Binary classification)
クラス数が2つのものを分類する。0か1かの二値で分類を行う。出力層のノード数は2に設定する。scikit-learnを使って学習させる場合、モデルのコンパイル時損失関数を以下のように設定する。
model.compile(loss="binary_crossentropy")
・多クラス分類(Multi-class classification)
クラス数が3つ以上のものを分類する。インデックスのつけ方は主に以下の二種類存在する。
Label encording
0か1か2か...で分類する。この数字はラベルと呼ばれ、「Tシャツ=0」「ズボン=1」「プルオーバー=2」というようにカテゴリ変数に割り当てられる。この場合、出力層のノード数はラベル数と同じ値に設定する。決定木やランダムフォレストで有効。
One-hot encording
カテゴリ変数に優劣や平均がないデータに対してlabel encordingを使った場合、モデルが間違って認識してしまい正しいモデルを作ることができない。例えば商品A、商品B、商品Cというカテゴリ変数に1、2、3というラベルを与えたとすると、1(A)よりも3(C)の方が良い製品、という間違ったモデルを生成してしまう。また、数字として扱うと品目の平均をとれることになるので、1(A)+2(B)+3(C)=6/3=2(B)となります。これは品名の平均は2(B)になる、という誤ったモデルが生成されてしまうことになる。これを防ぐためにone-hot encordingを行う。one-hot encordingはラベルを以下のようなone-hotベクトルに変換する。
1 → [1, 0, 0]
2 → [0, 1, 0]
3 → [0, 0, 1]
機械学習モデルの全体像
教師あり学習の手法
| 手法 | 回帰 | 分類 |
|---|---|---|
| 線形回帰 | ○ | × |
| ロジスティックス回帰 | △ | ○ |
| 決定木 | ○ | ○ |
| ランダムフォレスト | ○ | ○ |
| アダブースト | ○ | ○ |
| サポートベクターマシーン(SVM) | ○ | ○ |
| k-近傍法 | ○ | ○ |
| ニューラルネットワーク | ○ | ○ |
線形回帰
データの分布があるときに、そのデータに一番当てはまる直線を最小二乗法で求める手法。
ロジスティックス回帰
複数の変数から、ある事象が発生する確率を予測する。
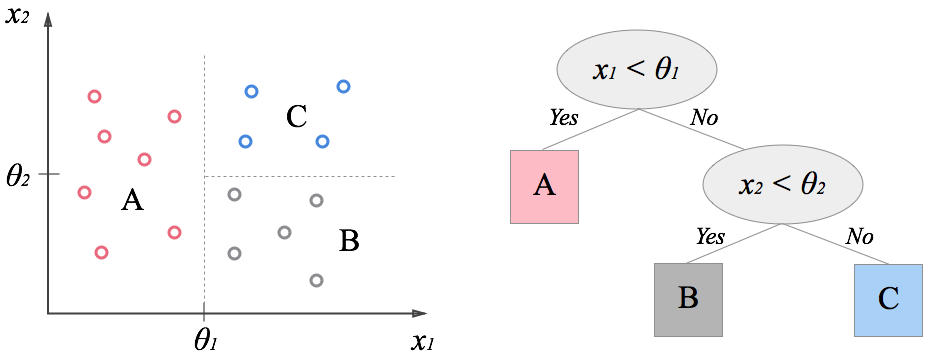
決定木
データから木構造の予測モデルを作る。下図において、赤い四角を縦線の境界線で◯か×に分類する際、どこが一番正答率が高くなるか繰り返し設定を行う。

メリット:
- 人間が理解しやすい
デメリット:
- 外れ値の影響を受けやすい
- 過学習になりやすい
- 決定木は確率的アルゴリズムを使うため、計算する期待値は推定であり、各結果の正確な予測ではない
ランダムフォレスト
決定木をたくさん作り、平均あるいは多数決をとって回答を導く。複数の決定木を用いられているので、決定木の短所である「過学習」を克服している。
ランダムフォレストの特徴
- 決定木を作る際にすべての訓練データを使わずに、一部の訓練データのみを使う
- 決定木を作る際にすべての特徴量を使用せず、決めた数の特徴量のみ使用する。
- ランダムフォレストは低バイアス・低バリアンスなモデルである
scikit-learnでは以下のようなパラメータを設定することが可能。
-
n_estimators:決定木の本数 -
max_features:特徴量のサブセットをランダムに選択するときの最大特徴量数。値を大きくするとランダムフォレスト中の決定木が似たようなものになり、値を小さくするとランダムフォレスト中の決定木はそれぞれ大幅に異なるものになる。 -
max_depth:決定木の深さ -
criterion:不純度評価指標
アダブースト
サポートベクターマシーン(SVM)
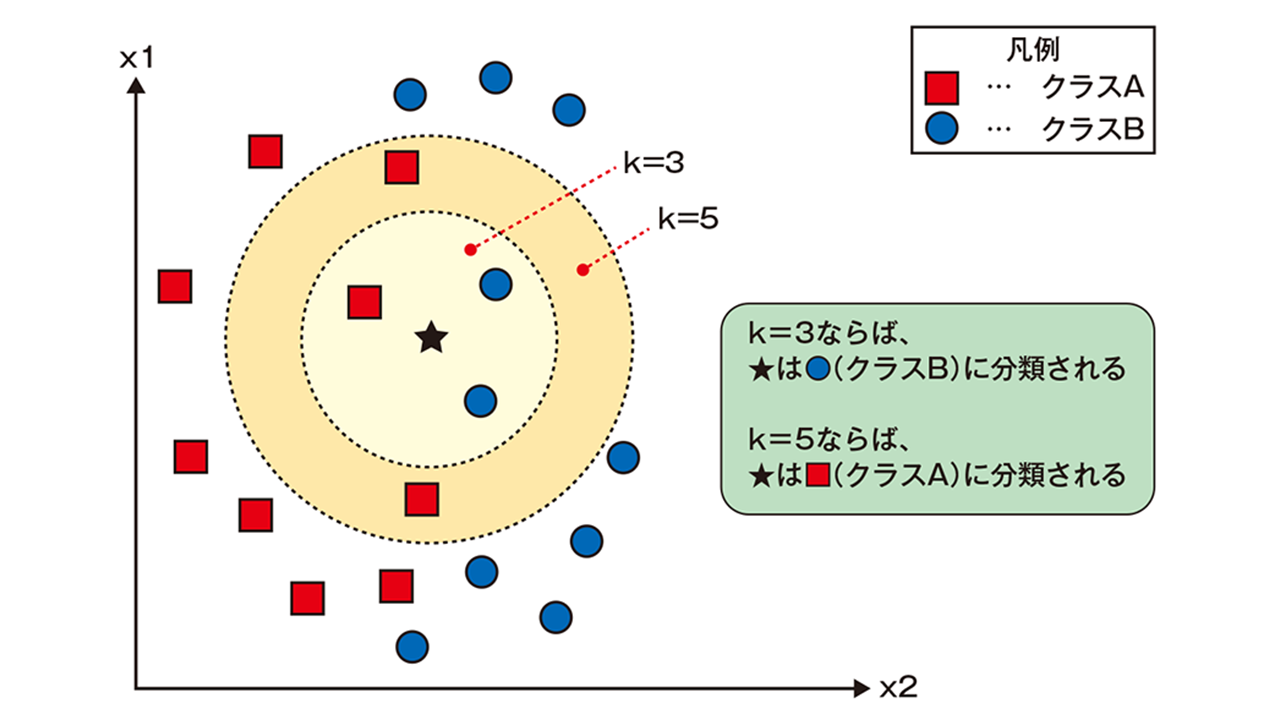
k-近傍法
k-近傍法とは多クラス分類に使われる手法の一つです。与えられた学習データをベクトル空間上にプロットしておき、未知のデータが得られたら、そこから距離が近い順に任意のk個を取得し、その多数決でデータが属するクラスを推定します。特にk=1のとき、k-最近傍法と言います。
ニューラルネットワーク
教師なし学習の手法
| 手法 | 目的 |
|---|---|
| k-平均法(k-means) | クラスタリング |
| X-平均法(X-means) | クラスタリング |
k-平均法(k-means)
クラスタリングに使われる手法。まずデータを適当なクラスタに分けた後、クラスタの平均を用いてうまい具合にデータがわかれるように調整させていく。
具体的な方法は以下の通り。
- 各点$x_i$に対してランダムにクラスタを割り振る
- 各クラスタに割り当てられた点について重心を計算する(画像の(b))
- 各点について上記で計算された重心からの距離を計算し、距離が一番近いクラスタに割り当て直す。(画像の(c))
- 2.と3.の工程を、割り当てられるクラスタが変化しなくなるまで行う
あらかじめクラスタ数を決めておく必要があることに注意
X-平均法(X-means)
k-平均法と似ているが、クラスタ数を設定する必要がない。クラスタ数はBICによる分割停止基準(?)を用いて自動的に決定される。
主成分分析
多すぎる変数を、より少ない指標や合成変数に要約する手法。このとき要約した合成変数のことを主成分と呼びます。多変量で多次元なビッグデータでも情報を損ないにくく、全体のイメージを可視化できることが特徴です。