1.この記事について
機械学習に関する本を一通り読み終えました。
復習の意味も兼ねて、
実際にモデルを作って検証をして、どうなったか見てみます。
2. 目的変数と説明変数
機械学習の世界では、以下の用語が出てきます。
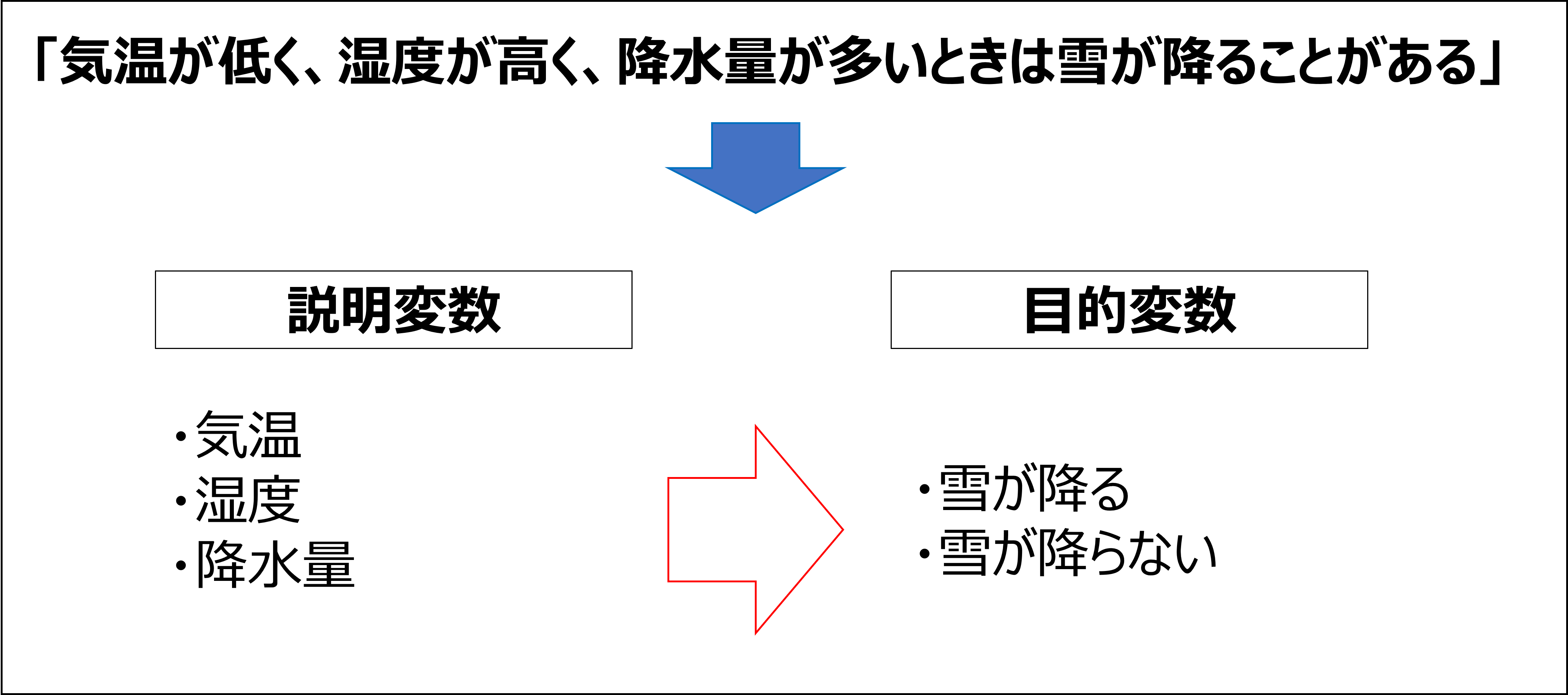
- 目的変数:予測したり、比較のベンチマークとしたいデータのこと。
- 説明変数:予測したり、比較のベンチマークとしたいデータと何らかの因果関係があると思われるデータのこと。
何か関係がありそうなデータ(説明変数)を利用して目的変数が実現できるのでは、
と当たりをつけるのが一般的なやり方です。
今回は、このような仮説を検証しますが、
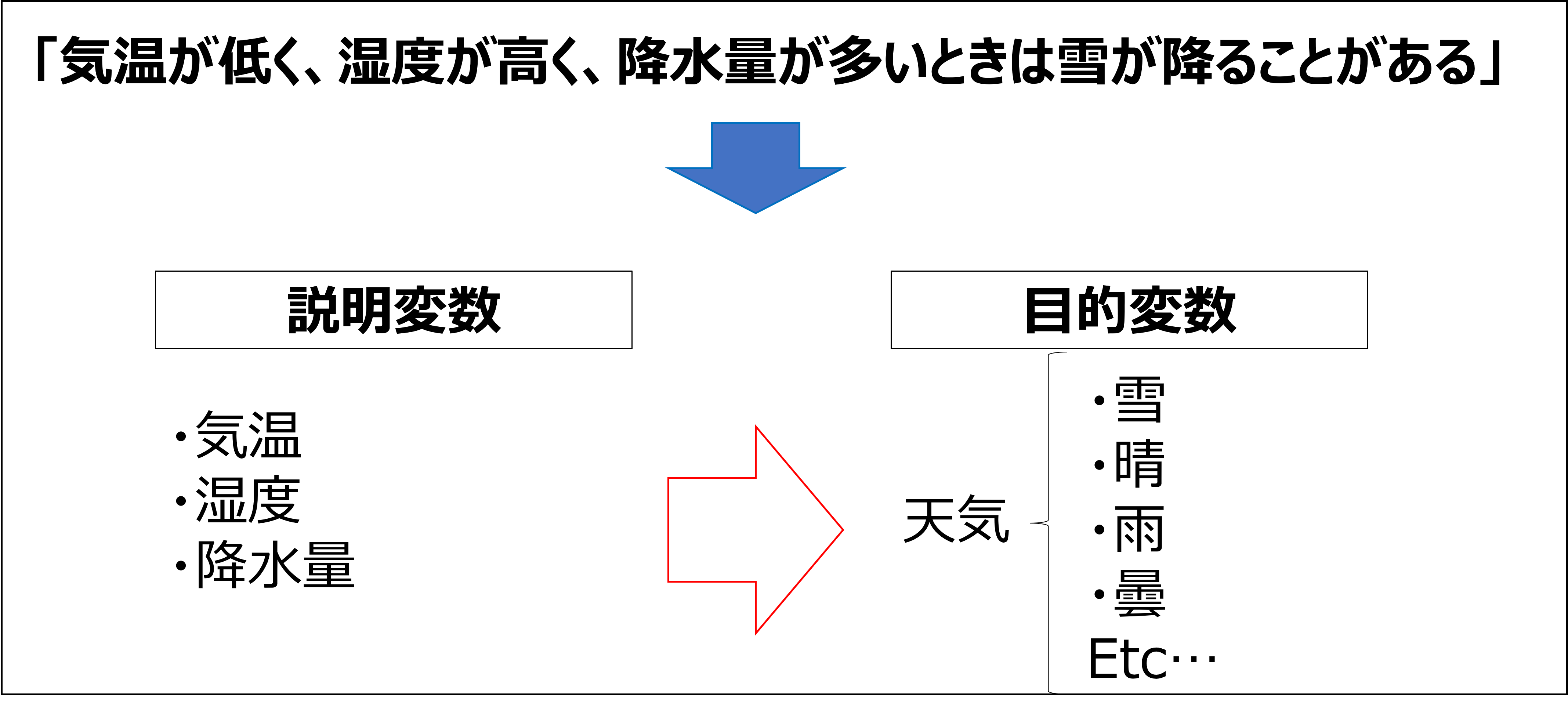
雪が降る/降らないで2値化してしまうと、他のどの天気と誤分類したのか
分からなくなってしまいます。
実際にモデルを作るときは、目的変数を「天気」にしました。
結論から言うと、
「雪と予測した時に本当に雪が降るのか?」
→この答えとしては、70%の確率で降っていました。
気象予報士が予測する天気予報の確率が70~80%と思えば、改善の余地はありますが、まずまずな出来になりました。
3.雪予測の進め方
これをやるには、理論を理解し、適切なプロセスを踏んでいく必要があります。
ただ、機械学習の過程を言語化すると、とても長い文章になるため、今回は図式化します。
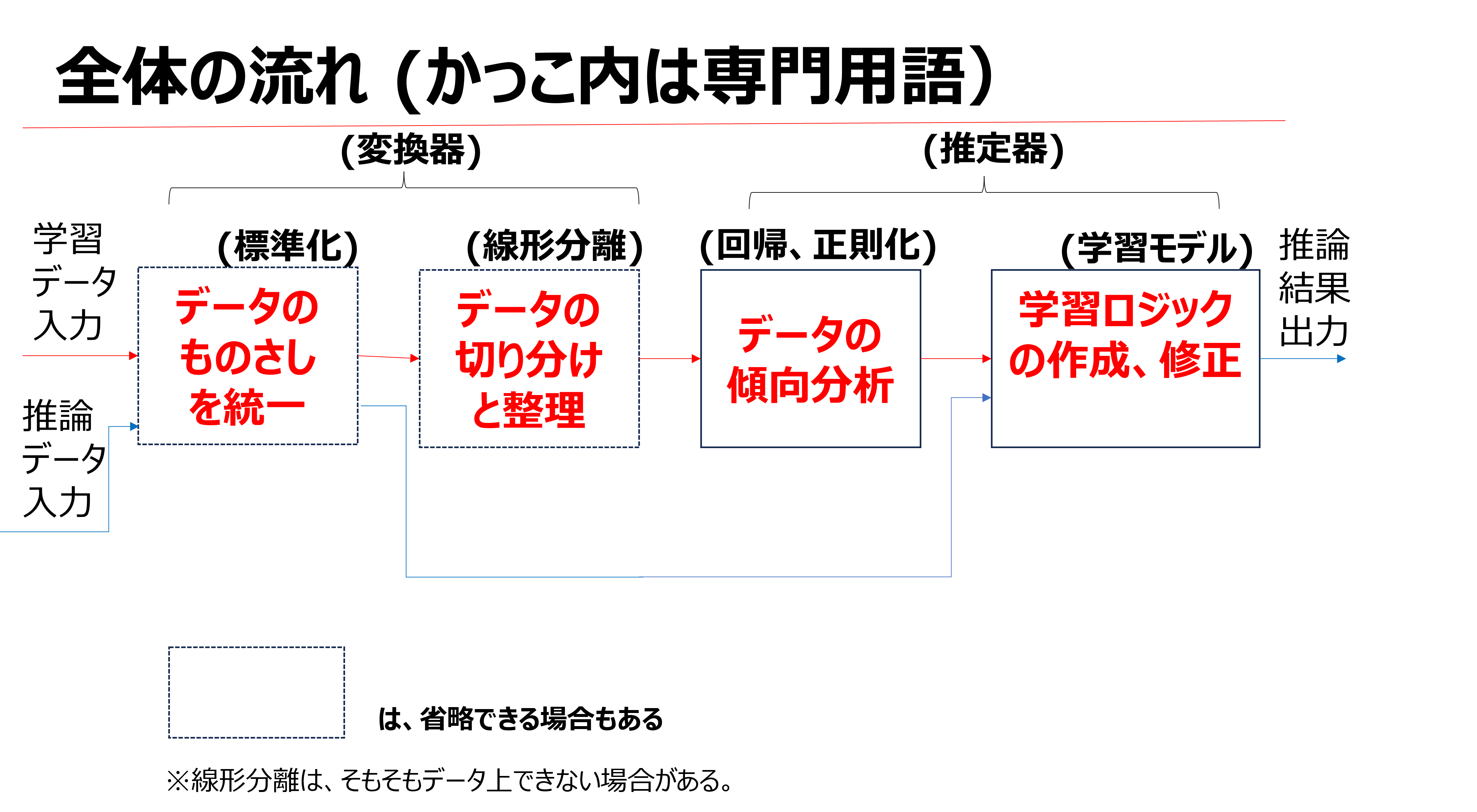
傾向が全く予測できないようなデータに対しては、
変換器と推定器の種類を変えて何度も試すことも有効です。
3.1 今回試す変換器の種類
標準化の手段
StandardScalerが一般的とされています。
例えば、説明変数が複数種類あって単純に比較できない時に使用できます。
元の説明変数の組み合わせが、確実にそのまま目的変数のデータに影響を及ぼす場合は、
標準化しなくていい場合もあります。
線形分離の手段
線形分離とは、あるデータを平面上にプロットしたときに、そのデータの
存在境界に線引きをできるようにすることです。
例えば、何らかの法則に従って
青丸のデータを「1番」、赤丸のデータを「2番」とラベル付けします。
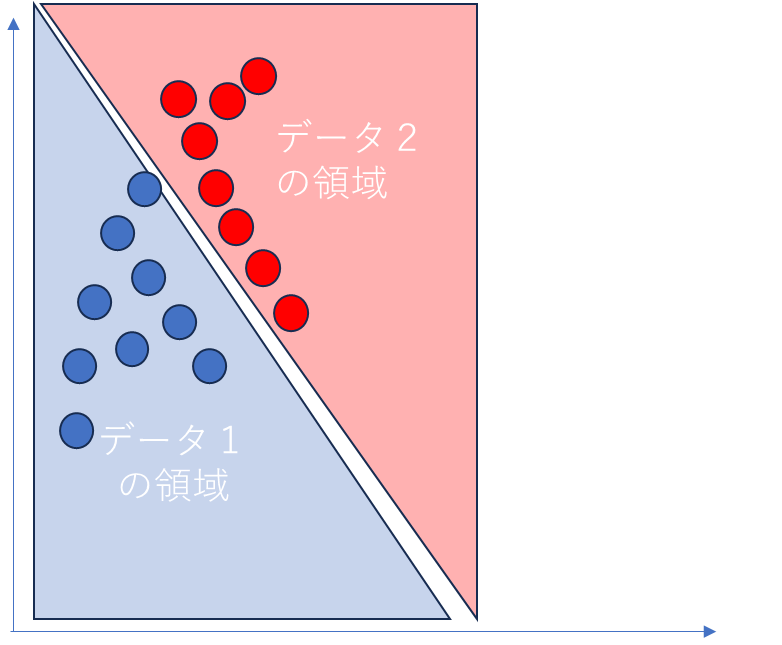
そうはいっても、上の図のようにきれいに境界が分かれることは稀です。
むしろ青と赤が複雑に入り混じって、まるで都道府県境のように境界が曲がっていることが多いです。
青と赤の境界が入り混じって、飛び地のようなものを作らないといけなくなった場合は、
線形分離が不可能と言います。
線形分離を不可能から可能にするには、データを加工するしかありません。
※どうにも線形分離できないデータもあります。
線形分離を可能にする方法は、以下2つが良く知られています。
- PCA(主成分分析)
⇒説明変数が複数あって入り乱れてる時、
目的変数に影響を及ぼす上位いくつかの説明変数を切り取る。
訓練データと学習データで分割できるときに有用。 - カーネルPCA
⇒説明変数のデータ同士で距離を測って、距離が近いところをランキング化し、
上位いくつかの説明変数を切り取る。
訓練データと学習データで分割できないときに有用。
アルゴリズムを、図式化すると下のようになります。
PCAとカーネルPCAでは出力も全く違うということに気を付ける必要があります。
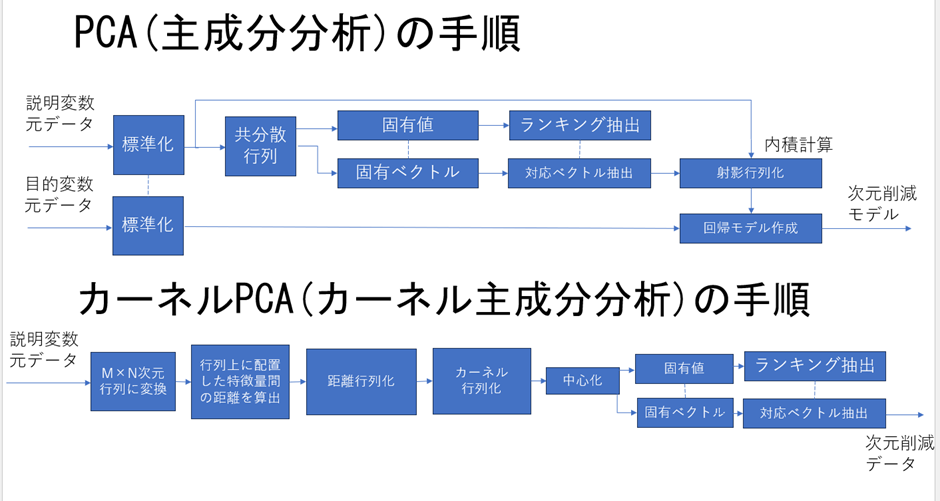
3.2 推定器の種類
教師無し学習と教師あり学習
-
教師無し学習
⇒分類問題・・・このデータはOKでこのデータはNG、と分類ができる法則を導き出す。
⇒回帰問題・・・このデータはこの程度上昇/下降する、と予測できる法則を導き出す。 -
教師あり学習・・・データに正解がない中で、何らかの法則を見つけ出すこと。
教師なし学習の分類問題の場合、
一般的な機械学習のアルゴリズムでは、下記のような構造になっています。
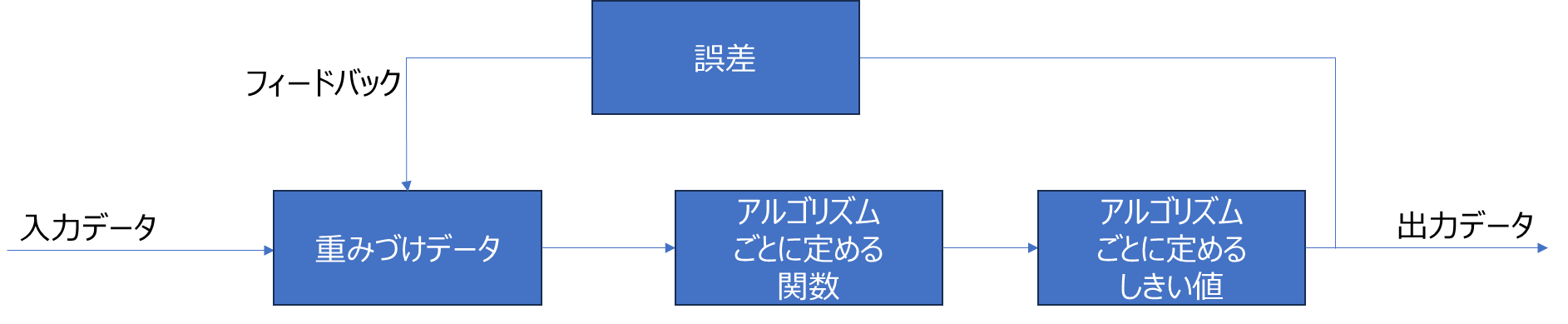
この仕組みを応用して、様々なアルゴリズムがあります。
詳細な仕組みは省略しますが、どのような用途に使われているか説明します。
| アルゴリズムの名前 | 主な用途 | メリット | デメリット |
|---|---|---|---|
| ロジスティック回帰 | 2値分類 | 2値分類の基礎的な方法で信頼性が高い | 3値以上の分類は使い方を工夫しないと精度が下がる |
| SVM | 2値分類 | 線形分離されたデータの境界にできるだけデータ群が近くなるようにまとめられる | 境界にどれだけ近づければ問題ないかは自分で調整し、自分で判断する必要がある |
| 決定木 | 2値分類、多クラス分類、回帰問題 | ロジックが統計に詳しくない人にも説明しやすく、汎用性も高い | 設定を最適化しないと誤った学習を必ず起こす |
| ランダムフォレスト | 2値分類、多クラス分類、回帰問題 | 決定木の学習精度を改善 | 設定を最適化しないと誤った学習を必ず起こす |
| LOF法 | 2値分類 | 正常と思われるデータが特定の値の周辺に固まる場合、簡単に分類できる | 正常パターンのデータを大量に収集しなければ、異常分類の精度が下がる |
| k近傍法 | 2値分類、他クラス分類 | データを多数決で推測するため、アルゴリズムがシンプル | 多数決で決めるデータは一気に読み込まないといけないため、メモリを圧迫する |
4.データについて
2018年12月中旬~2019年2月末までの富山市の天気データを利用し学習&推論しました。
説明変数:気温、温度、降水量、およびそれらの12時間前のデータ(計6種類)
目的変数:天気(晴/曇/雨/雪/雷 etc...)
5. モデルの候補選定
3.2で紹介した6つのモデルを利用します。
また、データの前処理として標準化の有無を比較しました。
なぜなら、気温/湿度/降水量の3つが降雪にダイレクトに影響を及ぼすならば、
数値をそのまま使えばいいはずであり、標準化はする必要がないからです。
6. モデル選定結果
モデルを評価する指標には、代表的なものが2つあります。
- 正解率
⇒推論したデータが実際のデータと比較してどれだけ正しかったか、の確率。 - 混同行列
⇒どの分類をどれだけ正解したか、間違えたかの確率。
どちらを採用するべきかは、ケースバイケースです。
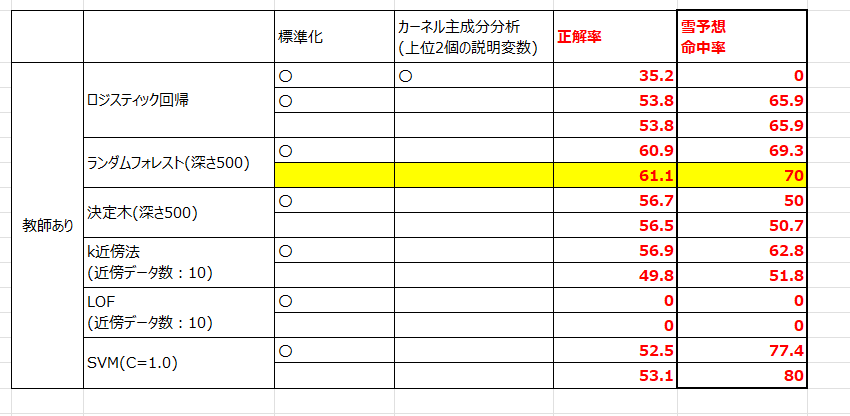
上の例では、両方算出しました。
SVMでは、雪予想だったときに本当に雪だった条件が80%となりました。
しかしながら正解率が非常に低くなっており、要するに予想外のタイミングで
大量の雪が降ったということになります。
このモデルは雪をジャストタイムに予想することが目的ですから、最も適切なものはランダムフォレストと思われます。
7. 考察
天気予報は多クラス分類です。
また、雪の条件と雨の条件が似ていることもあり、説明変数の気温/湿度/降水量を完全に線形分離することは極めて難しいと思われます。
とすると、アルゴリズムの特性からしてもランダムフォレストの正解率が高いのは当然の事と言えます。
ただし、雪の条件には上空の気圧なども少なからず影響するため、地上側の限られた情報では学習モデルがうまく機能しません。要するに、学習不足と言えます。
8. 結論
実際に機械学習を利用して学習モデルを構築する際は、やはり正しく学習モデルの特性を知ることが大事です。
それを知って初めてAIを作ろうかという話になります。
それでもデータが足りなかったりして、この例のように学習不足になってしまうことがあります。
事前の下調べが段取りとして極めて重要になることを認識していきたいと思います。