0. 使用言語
pypy3で基本提出してます。pypy3でTLEするときはpythonで提出してます。
(pypy3でTLEするときは、Decimal型や再帰関数を使うときなど。このときにpythonで提出してます)
1. ようやく到達
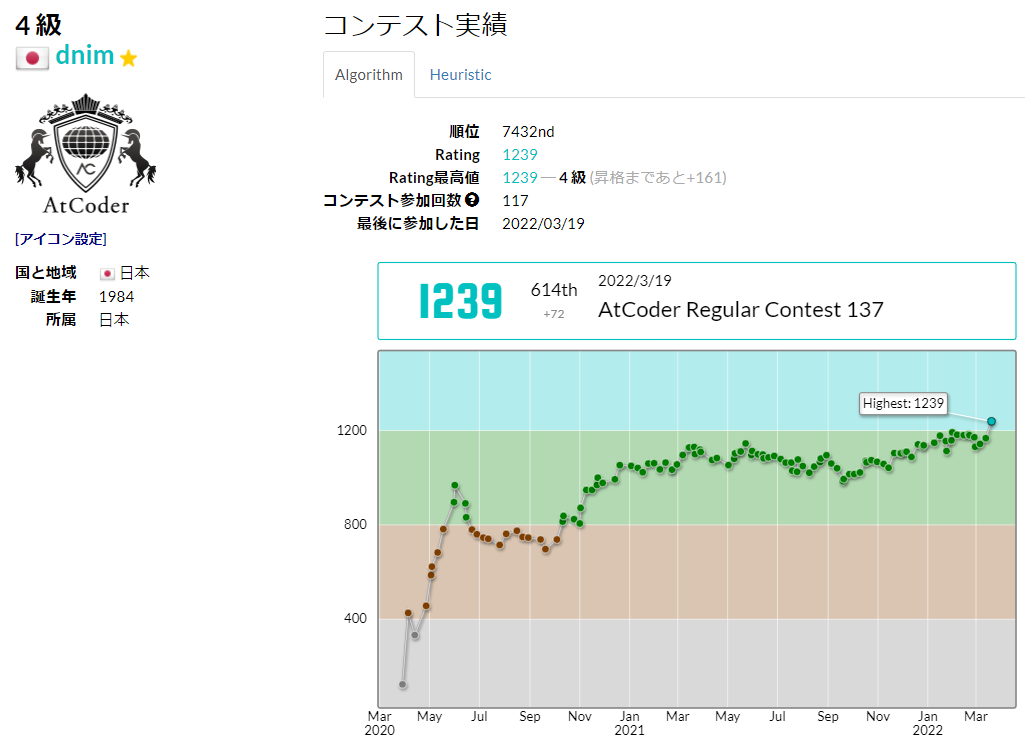
水色到達までものすごく時間かかりました。
緑まではすぐに行ったので、水色も行けるかと思ってたのですが、全然甘くなかったですね。
2020年3月28日から参加して、そこからほぼ毎週欠かさず参加しました。結果コンテスト参加回数117回。
毎週参加していたら、いつかは水色いけるだろうと思っていたのですが、
たまにパフォーマンスが水色行ったり、茶色になったりで、レートが上がったり下がったりの繰り返しで
1000~1100レート付近で往復してました。
2021年9月あたりで、一気に100レート溶かして、さすがに勉強しないと水色は無理だなと把握しました。
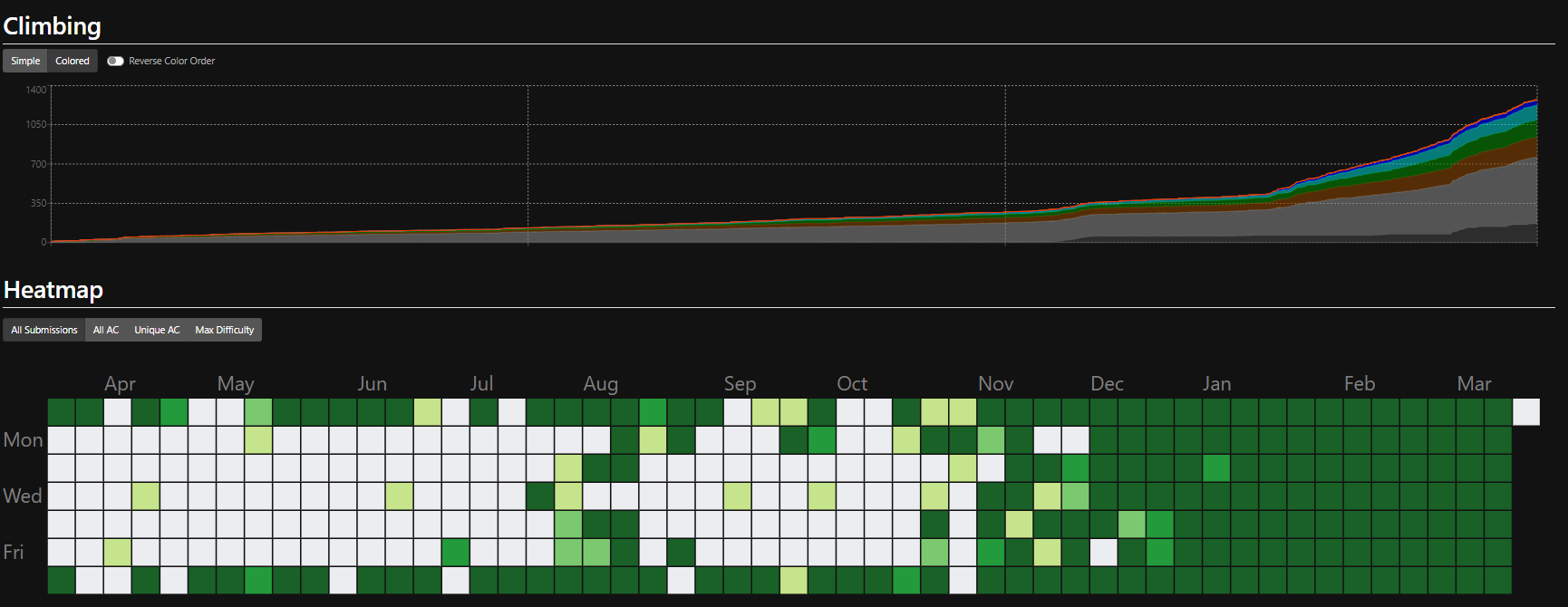
2021年10月付近から土日は数時間、平日は業務後数時間やり続けて毎日継続してました。
その結果、11月以降、緩やかではありますが、右肩上がりのレートになって、ようやく水色という感じです。
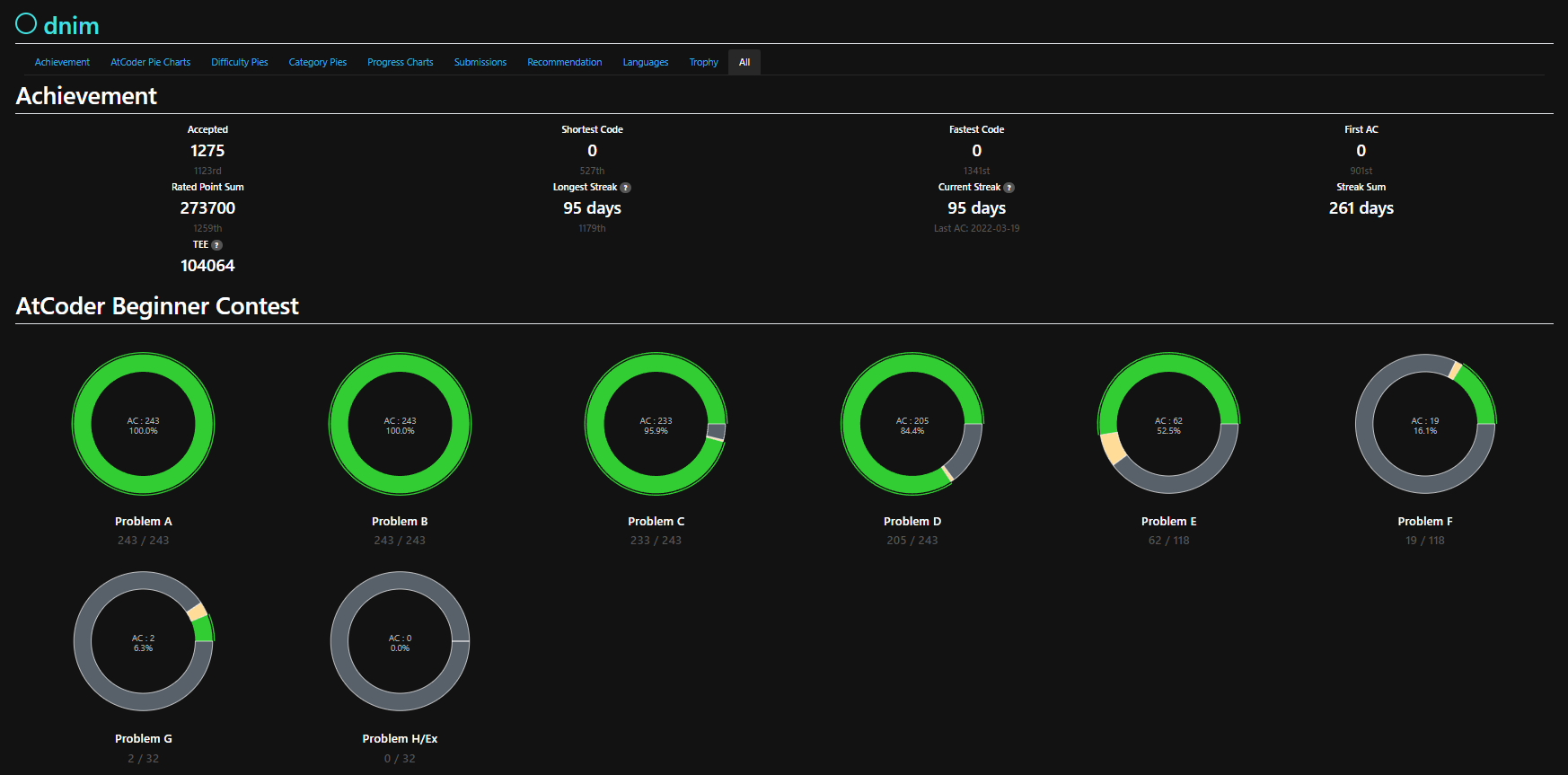
過去問1000問解けば、大体水色到達するといわれているのですが、私は1275問かかりました。
2. AtCoderをやった感想
プログラムを書く仕事をしているならば、AtCoderをやったほうがよいですね。メリットは一杯あります。
-
手作業よりプログラムを書いたほうが速いと判断するボーダーが下がる。
業務でログの整形など、書き捨てコードを書いて生産性を上げることはよくあると思いますが、
「プログラムを書く」という行為に自分自身の中でハードルが高いと、つい手作業でやってしまうことがあると思いますが
AtCoderで日頃プログラムを書いていると、そのハードルが低くなるので生産性が上がると思います。 -
よっぽどのことがない限り、業務でコーディングする内容はA, B, C問題あたりまで。
日頃の業務のプログラム実装であれば、AtCoderの問題のA, B, C問題が解けてたら十分かと思います。
A, B, C問題が早解きできる実力があれば、生産性の観点としては、プログラム開発の業務は任せてもらえるんじゃないかなと思います。
余談ですが、この前業務でUnionFind木を使いました。AtCoderをやって得た知識でしたので良かったです。 -
プログラムを書く速度が速くなる。
制御構文など基本的なコードをタイピングする速度が速くなりますね。これだけでも生産性は変わってくるかなと思います。
また、思った通りに動かなかったときの解析にかかる時間も短くなります。これも大きいですね。
これくらい実装速度は上がりました。問題まったく覚えてなかったのですが、想像以上に実力は上がってました。
やり続ける効果は大きいですね。

3. やったこと
2021年の10月付近から真剣に取り組みましたので、そのあたりから、やったことを書きます。
とりあえずAtcoder Beginner Contestは自分の実力で解ける問題を一通り解き、
1時間くらいかけて分からない問題は解説を見て解きました。解説見ても解けない問題は、ACしている人のコードを読んで理解ですね。
解けない問題の中で、考えないと分からない問題と知識がないと解けない問題があって、
とりあえず直ぐに効果が出る「知識がないと解けない問題」を解けるようにしました。
つまりライブラリの整備ですね。ABCDE付近の問題で良く使う関数は以下のものです。
3.1 グラフ理論
AtCoderで良く出てくるものって
・BFS
・DFS
・ダイクストラ
・ワーシャルフロイド
・トポロジカルソート
でしょうか。
不具合があったら申し訳ないですがコード貼っておきます。
(AtCoderでACされた人のコードをもらったりしてます)
・BFS, DFSのコード
from collections import deque
class Graph:
def __init__(self):
self.edges = {}
self.ansmod = 10 ** 9 + 7
self.path = [] # dfsでたどった経路
self.traverse_path = [] # dfsでたどり着けるノード順
def append_edge(self, sv, ev, weight = 1):
if sv in self.edges:
self.edges[sv].append((ev, weight))
else:
self.edges[sv] = [(ev, weight)]
def bfs(self, sv, N):
dist = [-1]*N
q = deque([])
q.append(sv)
dist[sv] = 0
connect_vtxs = []
cnt = [0] * N
cnt[sv] = 1
while len(q) > 0:
p = q.popleft()
connect_vtxs.append(p)
if p not in self.edges:
continue
for (ev, w) in self.edges[p]:
if dist[ev] != -1:
if dist[ev] == dist[p] + 1:
cnt[ev] += cnt[p]
cnt[ev] %= self.ansmod
continue
q.append(ev)
dist[ev] = dist[p] + 1
cnt[ev] = cnt[p]
return dist, connect_vtxs, cnt
def dfs(self, sv, N):
self.path = []
self.traverse_path = []
reached = [False] * N
q = deque([sv])
while q:
p = q.pop()
if p >= 0:
reached[p] = True
self.path.append(p)
self.traverse_path.append(p)
if p in self.edges:
for (ev, w) in self.edges[p]:
if reached[ev]:
continue
q.append(~p)
q.append(ev)
else:
self.path.append(~p)
・ダイクストラのコード
import heapq
class Dijkstra():
class Edge():
def __init__(self, _to, _cost):
self.to = _to
self.cost = _cost
def __init__(self, V):
self.G = [[] for i in range(V)]
self._E = 0
self._V = V
@property
def E(self):
return self._E
@property
def V(self):
return self._V
def add_edge(self, _from, _to, _cost):
self.G[_from].append(self.Edge(_to, _cost))
self._E += 1
def shortest_path(self, s):
que = []
INF = 10 ** 64
d = [INF] * self.V
d[s] = 0
heapq.heappush(que, (0, s))
while len(que) != 0:
cost, v = heapq.heappop(que)
if d[v] < cost:
continue
for i in range(len(self.G[v])):
e = self.G[v][i]
if d[e.to] > d[v] + e.cost:
d[e.to] = d[v] + e.cost
heapq.heappush(que, (d[e.to], e.to))
return d
・ワーシャルフロイドのコード(warshall_floyd_ansを呼ぶ。)
def warshall_floyd_k(vwc, N, d, k):
for i in range(N):
for j in range(N):
d[i][j] = min(d[i][j], d[i][k] + d[k][j])
return d
def warshall_floyd_ans(vwc, N):
inf = float('inf')
d = [[inf] * N for i in range(N)]
for i in range(N):
d[i][i] = 0
for i in range(len(vwc)):
v, w, c = vwc[i]
d[v - 1][w - 1] = c
d[w - 1][v - 1] = c
ans = 0
for k in range(N):
d = warshall_floyd_k(vwc, N, d, k)
return d
・トポロジカルソートのコード
import heapq
class Graph:
def __init__(self, N, M=-1):
self.V = N
if M >= 0: self.E = M
self.edge = [[] for _ in range(self.V)]
self.edge_rev = [[] for _ in range(self.V)]
self.topo_vertex_list = []
self.to = [0] * self.V
self.visited = [False] * self.V
def add_edge(self, a, b, cost=-1, bi=False, rev=False):
self.edge[a].append((cost, b))
if rev: self.edge_rev[b].append((cost, a))
if bi: self.edge[b].append((cost, a))
if not bi: self.to[b] += 1
def topo_sort(self): #topological sort
que = []
for v in range(self.V):
if self.to[v]==0: heapq.heappush(que, v)
while que:
v = heapq.heappop(que)
self.topo_vertex_list.append(v)
for (cost, u) in self.edge[v]:
self.to[u] -= 1
if self.to[u]: continue
heapq.heappush(que, u)
# 有向閉路を含まない有向グラフの根からの最長パスを求める。O(V + E)
def longest_dist(self):
self.topo_sort()
longest_dist_list = [0] * self.V
for u in self.topo_vertex_list:
for (_, v) in self.edge[u]:
longest_dist_list[v] = max(longest_dist_list[v], longest_dist_list[u] + 1)
return longest_dist_list
3.2 データ構造
よく使うデータ構造は、以下のものですね。
・Binary Indexed Tree
・Union Find
・Segment Tree
・SortedList
・Binary Indexed Treeのコード
class Bit:
def __init__(self, N = 0):
self.size = N
self.tree = [0] * (N + 1)
def sum(self, i):
s = 0
while i > 0:
s += self.tree[i]
i -= i & -i
return s
def add(self, i, x):
while i <= self.size:
self.tree[i] += x
i += i & -i
def inversion(self, arr): # listの要素に0があるとダメ
self.size = max(arr)
self.tree = [0] * (self.size + 1)
ans = 0
for i, a in enumerate(arr):
self.add(a, 1)
ans += i + 1 - self.sum(a)
return ans
def big_inversion(self, arr): # listの要素がとても大きいとき座圧する。
arrlist = list(set(arr))
arrlist.sort()
d = {}
for i in range(len(arrlist)):
d[arrlist[i]] = i + 1
newarr = []
for a in arr:
newarr.append(d[a])
return self.inversion(newarr)
・Union Find木のコード
# UnionFindは最小全域木を求めるのにつかえる。
# sameがTrueならすでにパスが存在するため追加しない
# sameがFalseなら辺を追加する意味でunionしてコストをカウントする。
# 最小コストの辺を追加していく
from collections import defaultdict
class UnionFind():
def __init__(self, n):
self.n = n
self.parents = [-1] * n
def find(self, x):
if self.parents[x] < 0:
return x
else:
self.parents[x] = self.find(self.parents[x])
return self.parents[x]
def union(self, x, y):
x = self.find(x)
y = self.find(y)
if x == y:
return
if self.parents[x] > self.parents[y]:
x, y = y, x
self.parents[x] += self.parents[y]
self.parents[y] = x
def size(self, x):
return -self.parents[self.find(x)]
def same(self, x, y):
return self.find(x) == self.find(y)
def members(self, x):
root = self.find(x)
return [i for i in range(self.n) if self.find(i) == root]
def roots(self):
return [i for i, x in enumerate(self.parents) if x < 0]
def group_count(self):
return len(self.roots())
def all_group_members(self):
group_members = defaultdict(list)
for member in range(self.n):
group_members[self.find(member)].append(member)
return group_members
def __str__(self):
return '\n'.join(f'{r}: {m}' for r, m in self.all_group_members().items())
・セグメント木のコード
class SegmentTree():
def __init__(self, n, op, e = 0):
self.n = n
self.op = op
self.e = e
self.log = (n - 1).bit_length()
self.size = 1 << self.log
self.d = [e] * (2 * self.size)
def update(self, k):
self.d[k] = self.op(self.d[2 * k], self.d[2 * k + 1])
def build(self, arr):
for i, a in enumerate(arr):
self.d[self.size + i] = a
for i in range(1, self.size)[::-1]:
self.update(i)
def set(self, p, x):
p += self.size
self.d[p] = x
for i in range(1, self.log + 1):
self.update(p >> i)
def get(self, p):
return self.d[p + self.size]
def query(self, l, r):
sml = smr = self.e
l += self.size
r += self.size
while l < r:
if l & 1:
sml = self.op(sml, self.d[l])
l += 1
if r & 1:
r -= 1
smr = self.op(self.d[r], smr)
l >>= 1
r >>= 1
return self.op(sml, smr)
・sortedListのコード(ものすごく長いので、参考URL貼ります)
# 構築にO(NlogN), 要素の追加、削除にO(logN), 検索もO(logN)
# https://raw.githubusercontent.com/cheran-senthil/PyRival/master/pyrival/data_structures/SortedList.py
3.3 その他
一杯あるので書ききれないですが、
・LIS
# 最長部分増加列の長さを求める (ai < ajとなる部分増加列)
from bisect import bisect_left
def LIS(L):
seq = []
for ai in L:
pos = bisect_left(seq, ai)
if len(seq) <= pos:
seq.append(ai)
else:
seq[pos] = ai
return len(seq)
・区間スケジューリング
def maxCntIntervalScheduling(l):
l.sort(key = lambda x: x[1])
r1 = l[0][1]
cnt = 1
for i in range(1, len(l)):
l1, r2 = l[i]
if l1 >= r1:
cnt += 1
r1 = r2
return cnt
・二項係数の計算(comb_initの戻り値を使ってcombを高速計算)
# nCkのnの最大値をcomb_initで初期化しておけば、
# nCkは瞬時に求められる。
# combのための初期化
def comb_init(n, mod):
fac = [0] * (n + 1)
finv = [0] * (n + 1)
inv = [0] * (n + 1)
fac[0] = 1
fac[1] = 1
finv[0] = 1
finv[1] = 1
inv[1] = 1
for i in range(2, n + 1):
fac[i] = fac[i - 1] * i % mod
inv[i] = mod - inv[mod % i] * (mod // i) % mod
finv[i] = finv[i - 1] * inv[i] % mod
return fac, finv
# comb_initの戻り値を引数にセット
# 10 ** 7くらいまでならO(1)
def comb(n, k, mod, fac, finv):
if n < k:
return 0
if (n < 0) or (k < 0):
return 0
return (fac[n] * ((finv[k] * finv[n - k]) % mod)) % mod
・二項係数の計算(Nが大きくてKが小さいとき(Nが10 ** 9程度でKは1000程度))
# Nが大きくて、Kが小さいときのcomb関数
# nCkのkの最大値をコンストラクタで与える。
class CombinationCount():
def __init__(self, Kmax, mod):
self.mod = mod
self.modinvlist = [1] * (Kmax + 1)
for k in range(1, Kmax + 1):
self.modinvlist[k] = self._modinv(k, ansmod)
def _modinv(self, a, m):
b, u, v = m, 1, 0
while b:
t = a // b
a -= t * b
a, b = b, a
u -= t * v
u, v = v, u
u %= m
if u < 0:
u += m
return u
# O(K)
def comb(self, N, K):
if K == 0:
return 1
if K == 1:
return N % self.mod
ans = 1
for r in range(1, K + 1):
ans *= (N - r + 1) * self.modinvlist[r]
ans %= self.mod
return ans
・拡張ユークリッドの互除法による逆元計算
# 拡張ユークリッドの互除法による逆元計算
# ax ≡ 1 (mod m)のxを求める
# 4x ≡ 1 (mod 13)を求めるときは、modinv(4, 13)とすればxが求まる
def modinv(a, m):
b, u, v = m, 1, 0
while b:
t = a // b
a -= t * b
a, b = b, a
u -= t * v
u, v = v, u
u %= m
if u < 0:
u += m
return u
・約数列挙
# 約数を列挙
def make_divisors(n):
lower_divisors , upper_divisors = [], []
i = 1
while i*i <= n:
if n % i == 0:
lower_divisors.append(i)
if i != n // i:
upper_divisors.append(n//i)
i += 1
return lower_divisors + upper_divisors[::-1]
・素因数分解
# 前処理しておくと素因数分解が早いコード
import collections
MAXN = 10**6
sieve = [i for i in range(MAXN+1)]
p = 2
while p*p <= MAXN:
if sieve[p] == p:
for q in range(2*p,MAXN+1,p):
if sieve[q] == q:
sieve[q] = p
p += 1
def prime(a):
tmp = []
while a > 1:
tmp.append(sieve[a])
a //= sieve[a]
return collections.Counter(tmp)
・約数個数列挙
# MAXNまでの約数個数列挙
MAXN = 10 ** 7
div = [0] * (MAXN + 1)
for n in range(1, MAXN + 1):
for m in range(n, MAXN + 1, n):
div[m] += 1
・bit全探索。全通りチェックしたいとき。(データ数が大きいとTLEになる)
# 全通りパターンチェック
# Nはパターン、種類の数。
from itertools import combinations
# combinationsの中のrange(1, N + 1)を特定のリストにすれば、全通り出来る。
for n in range(1, N + 1):
for comb in combinations(range(1, N + 1), n):
for c in comb:
# ここに選ばれたパターンの組みを1つずつ見ていける
あと、アルゴリズムの考え方としては
・imos法
・しゃくとり法
・動的計画法
などでしょうか。(関数化が難しいので、内容を理解してコード書けるようにする)
4. 本番前に用意してるコード
以下のコードをベースにして問題を解いています。
問題によって大きい数値を扱うとき、10 ** 9 + 7か998244353の余りを求めるので
先頭にコメントアウトで定義してます。
デバッグしたコードをそのまま提出してWAという悲しいことを防ぐために
debug_print関数を用意してます。AtCoderは標準エラー出力にすれば、デバッグコードありでも
ACになるんですよね。できればデバッグコード消しておきたいですが。実行時間が遅くなるので。
あとは問題の入力仕様によって、main関数の実装を適当に使ってます。
resolve関数を介してmain関数を呼び出しているのは、AtCoderのUnit Testツールを使っているからですね。これ便利で、A, B, C問題でサンプルがWAのまま提出するというようなことがなくなります。
サンプルが通ったら自動提出するようなツールもあるようですが、
私はサンプル通ってから少しほかの入力データで動作確認したいときもあるので、そのツールは使っていないですね。
あとpypy3は再帰が遅いのであまり再帰関数を実装したくないですが、以下のコードを書くと、多少速くなるそうです。
import pypyjit
pypyjit.set_param('max_unroll_recursion=-1')
これがいつも使っているコードです。
(2022/05/07 alpha関数が間違っていたため修正。(iとjが逆になっていた。))
# ansmod = 10 ** 9 + 7
# ansmod = 998244353
import sys
def debug_print(*args):
print(args, file = sys.stderr)
def accmod(arr, M, inizero = False):
a = [0]
for ar in arr:
a.append((a[-1] + ar) % M)
if not inizero:
a = a[1:]
return a
def acc(arr, inizero = False):
a = [0]
for ar in arr:
a.append(a[-1] + ar)
if not inizero:
a = a[1:]
return a
def alpha():
return "abcdefghijklmnopqrstuvwxyz"
def alpha_num(s):
return ord(s) - ord("a")
def alpha_big():
return "ABCDEFGHIJKLMNOPQRSTUVWXYZ"
def alpha_big_num(s):
return ord(s) - ord("A")
# Queryを並び変えて問題を解くときは、答えのインデックスを3つめに追加しておく
def input_query_data(Q):
f = sys.stdin
LR = []
for q in range(Q):
l, r = map(int, f.readline().split())
LR.append([l, r, q])
return LR
def init_tbl(H, W, val=0):
return [[val] * W for i in range(H)]
# 「#」がもの、「.」が何もないとすると、一回り周辺を「.」で埋める
# マップを作成する。「.」が0で「#」が1を表す
def create_map(H, W):
f = sys.stdin
S = [f.readline().rstrip() for i in range(H)]
tbl = [[0] * (W + 2) for i in range(H + 2)]
for i in range(1, H + 1):
for j in range(1, W + 1):
tbl[i][j] = 0 if S[i - 1][j - 1] == "." else 1
return tbl
from collections import Counter
def counter_elem(l):
return Counter(l)
def sumk(n):
return n * (n + 1) // 2 if n >= 1 else 0
def sumk2(n):
return n * (n + 1) * (2 * n + 1) // 6 if n >= 1 else 0
def power(n, r, mod):
if r == 0: return 1
if r%2 == 0:
return power(n*n % mod, r//2, mod) % mod
if r%2 == 1:
return n * power(n, r-1, mod) % mod
def YN(cond):
return "Yes" if cond else "No"
from operator import itemgetter
def sorted_idx(a, idx): # 0 origin
return sorted(a, key = itemgetter(idx))
def popcount(x):
x = x - ((x >> 1) & 0x55555555)
x = (x & 0x33333333) + ((x >> 2) & 0x33333333)
x = (x + (x >> 4)) & 0x0f0f0f0f
x = x + (x >> 8)
x = x + (x >> 16)
return x & 0x0000007f
import bisect
def search_min_diff(l, val):
ans = 10 ** 64
idx = bisect.bisect_left(l, val)
for k in range(-1, 2):
if 0 <= idx + k < len(l):
ans = min(ans, abs(val - l[idx + k]))
idx = bisect.bisect_right(l, val)
for k in range(-1, 2):
if 0 <= idx + k < len(l):
ans = min(ans, abs(val - l[idx + k]))
return ans
def compcoord(l):
sl = sorted(set(l))
d = { v: i for i, v in enumerate(sl) }
revd = [-1] * len(sl)
for k, v in d.items():
revd[v] = k
return d, revd
# import pypyjit
# pypyjit.set_param('max_unroll_recursion=-1')
# sys.setrecursionlimit(2000000)
def main():
f = sys.stdin
N = int(f.readline())
A = list(map(int, f.readline().split()))
S = f.readline()[:-1]
N, M = map(int, f.readline().split())
H, W = map(int, f.readline().split())
xyc = [list(map(int, f.readline().split())) for i in range(N)]
SS = [f.readline()[:-1] for i in range(N)]
Edges = [list(map(lambda x:int(x) - 1, f.readline().split())) for i in range(N)]
Strs = f.readline()[:-1].split()
tmp = init_tbl(H, W)
def resolve():
print(main())
# print(main() % ansmod)
if __name__ == '__main__':
resolve()
5. 今後の予定
今後も毎日問題を解き続けていこうと思います。次は1400レート、その次は青色を目指したいと思います。
青レートに行くためには、おそらく今解いている問題数に+1問しないと上がれないと思うので
水色diff~青diff中心に勉強しないといけないのかなと思います。
青色到達した人の記事なども参考にしようと思います。