生活していると、与えられたグラフの全ての節点を訪問して何らかの処理を行わなければならない状態になることがあると思います。そのような場面で使えるアルゴリズムに深さ優先探索があるので勉強していたのですが、一つ疑問が湧いてきたので調べたメモです。
グラフを表す隣接リストLを与えられて、深さ優先探索によって頂点を訪問していくコードを、アルゴリズムクイックリファレンスに記載の擬似コードを見ながら python で以下のように実装した。一般に、深さ優先探索のコードは細かい違いはあってもだいたいこんな感じになると思う。
def dfs(L, colors, v):
colors[v] = 'grey'
for nv in L[v]:
if colors[nv] == 'white':
dfs(L, colors, nv)
colors[v] = 'black'
if __name__ == "__main__":
L = [
[1],
[2, 3],
[],
[2]
]
colors = ['white'] * len(L)
dfs(L, colors, 0)
このコードでは、節点の状態を3つに分類し、
-
white:未訪問 -
grey:その節点から先にある節点(これらの節点を descendants と呼ぶ)を再帰的に訪問中 -
black:その節点のすべての descendants を訪問済み
と色分けして扱っている。しかし、冷静に考えると上記のコードではgreyと blackをわざわざ分けて考える必要がないことに気づく。コード中で節点の状態を使っているのは、if文で節点の状態がwhiteかどうかで分岐しているところだけなので、必要な情報は「節点がwhiteかそうでないか」だけであり、greyとblackの区別が何も役立っていない。つまり、greyとblackをまとめて"訪問済みの節点"として扱ってもプログラムの機能に何も変わりがないことになる。
その割に、深さ優先探索の実装例を調べるとgreyとblackを区別しているものが多い。ということで、なぜgreyという状態が必要か検索したら以下のページにわかりやすい回答があったのでまとめておく。
The purpose of grey node in graph depth-first search
greyとblackの区別が必要な場面の一つの例として、有向グラフ中の閉路を検出したい場合が考えられる。無向グラフだと、「訪問中の節点の隣に(blackであろうがgreyであろうが)訪問済みの節点があるならば、閉路がある」ことになる。しかし、有向グラフだとそうとは限らない。
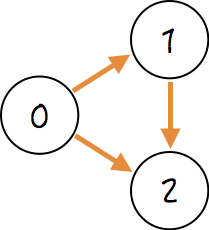
例えば、以下の閉路を持たない有向グラフを深さ優先探索しながら閉路を検出することを考える。
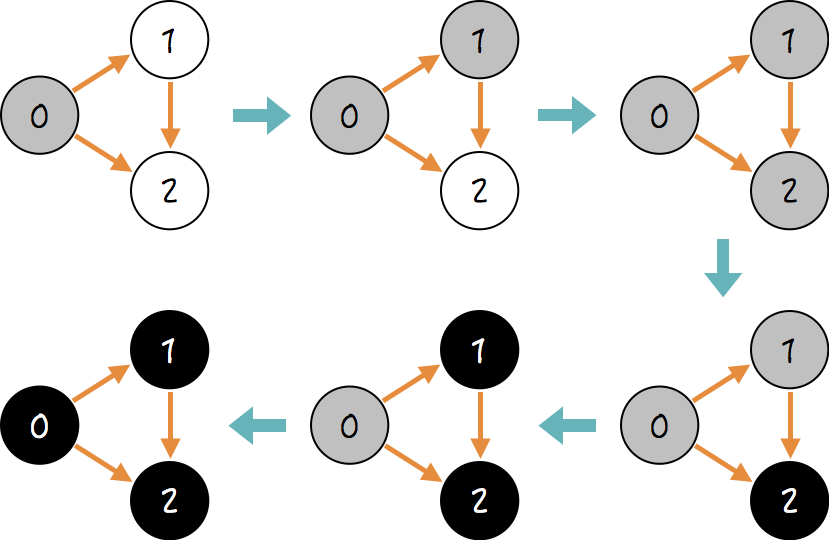
隣接する節点のうち数字が小さいものから順に訪問していく深さ優先探索をすると、節点の状態の変化は以下のように変化していく。
一番左下の最後の状態で、節点0から見て2が隣接する訪問済みの節点なので、単に「隣接する訪問済みの節点がある」という無向グラフと同じ基準で閉路を検出してしまうと、この例のような閉路がないグラフでもあるということになってしまうのである。
グラフにおいて「閉路がある」ということは、「ある節点から descendants を辿っていき、自分自身に到達可能であること」と言い換えることができる。これはすなわち、「自分が自分の descendant であるような節点が存在する」ということである。この条件を深さ優先探索の3つの状態white、grey、blackと考え合わせてみると、閉路がある条件として、「現在訪問中の節点から到達できる、隣接する grey の節点が存在する」と考えてよいことがわかる。
これを理解するために、現在訪問中の節点を A、隣接するgreyの節点を B として具体的に考えてみる。A は現在greyの状態にあるすべての節点の descendant であるから、当然greyである B の descendant である。この B の descendant である A から B に到達できることから、 B は B 自身の descendant であり、閉路が存在することになる。
一方で、現在訪問中の節点に、到達できてかつ隣接するblackの節点が存在しても閉路があると言えないことに注意。これは、現在訪問中の節点がblackの節点の descendant ではないことから、上の議論が成り立たないためである。
以上の基準に従うと、上の3つの節点からなるグラフの例で言うと、最後の状態で節点0から見て2はgreyではなくblackなので、「現在訪問中の節点から到達できる、隣接する grey の節点が存在する」という基準をもとに、ちゃんと閉路の有無を判定できることになる。当然、この基準を使うためにはgreyとblackという状態を分けて扱わなければならないので、greyとblackの節点を区別することが閉路を検出することに役立つことがわかった。
他にもgreyとblackを区別する意味がある具体例があったら教えてください。