主成分分析の2つの定式化

#(まえがき)
勉強の整理として書いてます．間違いを発見された方は，どうか__優しい言葉で__ご指摘ください．
そこの強い人! 見て見ぬ振りはダメですよ~~~

主成分分析とは

(今回は低ランク近似についてはあまり触れてません)
　主成分分析(Principal Component Analysis, PCA)についてwikipediaで検索してみると以下のように書かれています．

Principal component analysis (PCA) is a statistical procedure that uses an orthogonal transformation to convert a set of observations of possibly correlated variables (entities each of which takes on various numerical values) into a set of values of linearly uncorrelated variables called principal components.
(principal component analysis (wikipedia))

変数間に相関がありそうなデータ行列を直交変換することで，主成分と呼ばれる__相関のない変数群を生成する方法__と書かれています．...何を言ってるのでしょうか?

#雑なイメージ
　以下のようなデータの散布図が得られたとします．

　以降縦軸をy軸，横軸をx軸と呼ぶことにします．主成分分析は，この__散布の散らばり具合(=分散)が最大になるような新しい軸をデータの変換によって作る手法__です．例えば，

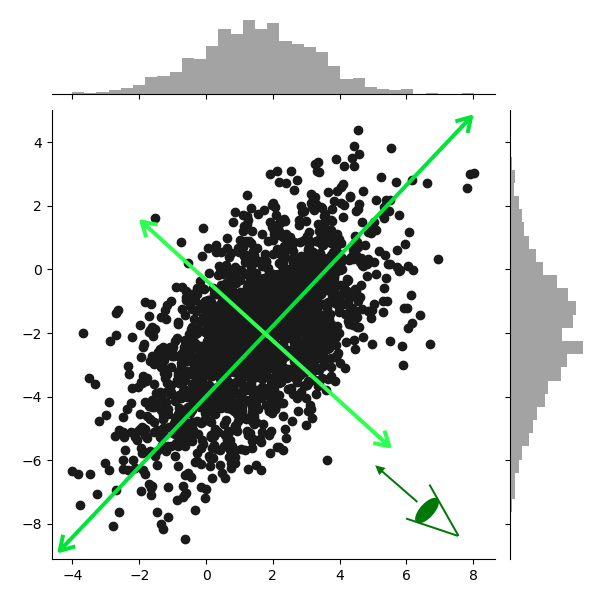
こんな感じの軸を作ることを目的としています．目のところから見ると，長い方の軸が，データの散らばりを表す新しい軸となっていることがわかります．このような軸をどう作るか(e.g.どんな制約のもと，どういった損失関数を用いるか)の方針設定を定式化と呼んでいます(私だけかもしれません．)
※この図の短い方の軸は，1本目の長い方の軸に直交するように作られています．3本目は1,2本目に直交するように，4本目は1,2,3本目に直交するように...以下同じように作られていきます．

##おまけ: ベクトルが直交する=無相関?
　高校数学では，3次元ベクトル(別に2次元でもいいです)の内積は$$a\cdot b = a_1b_1+a_2b_2+a_3b_3$$だったり，$$a\cdot b=|a||b|cos\theta\tag{1}$$と表されていました．ここで，$\theta$はaとbの間の角度を表しています．ここで，a,bが中心化されている(e.g.$\bar{a}=\bar{b}=0$)として，(1)式を$cos\theta$の式に書き換えると

\begin{eqnarray}
cos\theta&=&\frac{a\cdot b}{|a||b|}\\
&=&\frac{a_1b_1+a_2b_2+a_3b_3}{\sqrt{a_1^2+a_2^2+a_3^2}\sqrt{b_1^2+b_2^2+b_3^2}}\\
&=&\frac{\sum_{i=1}^3 a_ib_i}{\sqrt{\sum_{i=1}^3a_i^2}\sqrt{\sum_{i=1}^3b_i^2}}\\
&=&\frac{\sum_{i=1}^3 (a_i-\bar{a})(b_i-\bar{b})}{\sqrt{\sum_{i=1}^3(a_i-\bar{a})^2}\sqrt{\sum_{i=1}^3(b_i-\bar{b})^2}}\\
&=&\frac{Cov(a,b)}{\sqrt{\sigma_a^2}\sqrt{\sigma_b^2}}\\
&=& Corr(a,b)
\end{eqnarray}

と結局は$cos\theta$と相関係数$Corr(a,b)$が一致します．ここで，ベクトルが直交するとき$\theta=90^\circ$であり，$cos90^\circ=0$となることから$Corr(a,b)=0$となり，２つのベクトルは無相関となります．
#以下で使用する記号などなど
以下の主成分分析の定式化に利用する記号を先に書いておきます．

• X: データ行列($N\times p$)，行が観測点や個体，列が項目や変数を表します
• $x_i$: データ内のi番目の個体($p\times 1$)
• W: 重み行列($p\times m$)，$m\le p$, $W^TW=I_m$とします
• $w_j$: j番目の重み($p\times 1$)
• L: 主成分の負荷量行列($p\times m$)．主成分得点の重みづけをします
• F: 主成分得点行列($n\times m$)，$F^TF=NI_m$
• $f_i$: i番目の個体の主成分得点．
• E: 残差行列
• $e_i$: i番目の個体の残差(Lと$f_i$で説明されなかった部分みたいな)
• $||A||_F^2 = trA^TA=trAA^T$: frobeniusノルム．

これも先に書いておきますが以下の説明は割と雑です．がさつな人間なので...
(ちなみにどっちの定式化も深いところではほとんど同じです．)

##方針1: 元のデータの分散を最大化するような直交変換の仕方を求める
　まずは元のデータの直交変換によって分散を最大化する方針について考えます．元のデータをX($N$個体$\times$$p$変数の行列,列中心化してるとします)とすると，Xの共分散行列Sは

S := \frac{1}{N}X^TX

で定義されます．話を単純にするために，まず第一主成分(さっきの長い方の軸)だけを求めることを考えます．上で定義したように制約$W^TW = I_m$(=Wは列直交行列)から$w_i$は

\begin{eqnarray}
w_i^Tw_j = \left\{
\begin{array}{l}
1 & for \ i = j\\
0 & for  \ i \ne j
\end{array}
\right.
\end{eqnarray}

を満たさなければならないことがわかります．よって$w_1$は$w_1^Tw_1=||w_1||^2 = 1$という制約を満たすように定めなければなりません．では，最適化問題の形に書き換えます．

\begin{eqnarray}
\underset{||w_1||^2=1}{max} w_1^TSw_1 &=& \frac{1}{N}(Xw_1)^T(Xw_1)\\
&=& \frac{1}{N}||Xw_1||^2
\end{eqnarray}

この問題をラグランジュの未定乗数法(method of Lagrange multiplier，wiki)によって解きます．ラグランジュ関数は

L(w_1,\lambda_{11}) = \frac{1}{N}||Xw_1||^2 - \lambda_{11}(||w_1||^2-1)

で，$w_1$の最適値は微分して0と置くことで求まります．

\begin{eqnarray}
&\frac{\partial}{\partial w_1}L(w_1,\lambda_{11})=\frac{2}{N}X^TXw_1 - 2\lambda_{11} w_1 =0\\
&\Leftrightarrow  Sw_1 = \lambda_{11} w_1
\end{eqnarray}

$w_1$を求めるための問題は，Sの最大固有値を求める問題に帰着しました．後はこの固有値問題を解けば，$w_1$はSの最大固有値に対応する固有ベクトルとして求めることができます．そして得られた$w_1$によって第1主成分得点(さっきの長い方の軸)は$Xw_1$で与えられます．(この節の以下あまり自信ないので参考にする際は正しいかどうか注意して利用してください)
第2~m主成分得点に関する重み$w_2,\cdots,w_m$を求めるために，先ほどの$w_1$のみに関する最適化問題を拡張します．

\begin{eqnarray}
\underset{||w_i||2=1,w_i^Tw_j=0}{max} \frac{1}{N}||Xw_i||^2
\end{eqnarray}

この問題に対するラグランジュ関数は，

\begin{eqnarray}
L(w_i,\Lambda) &=& \frac{1}{N}||Xw_i||^2 - \lambda_{ii}(||w_i||^2-1) - \sum_{i\ne j}\lambda_{ij}w_i^Tw_j\\
\end{eqnarray}

先ほどと同様に，$W$の最適値はこの関数を偏微分して0と置くことで求まります．

\begin{eqnarray}
&\left\{
\begin{array}{l}
\frac{\partial}{\partial w_i}L(w_i,\Lambda) = 0\\
\frac{\partial}{\partial w_j}L(w_i,\Lambda)=0\ (j=1,\cdots,m)\tag{1}\\
\frac{\partial}{\partial \lambda_{ii}}L(w_i,\Lambda)=0\\
\frac{\partial}{\partial \lambda_{ij}}L(w_i,\Lambda)=0\ (j=1,\cdots,m)
\end{array}
\right.\\
&\Leftrightarrow Sw_i = \lambda_{ii}w_i
\end{eqnarray}

上の連立方程式の2番目と3番目から，$\lambda_{ij}=0(i\ne j)$であることが分かります．先ほどの$w_1$の場合と同様に共分散行列Sの固有値問題に帰着しました．つまるところ固有値分解すれば重み行列は求まることが分かりました．ちなみに主成分得点行列は$XW$で求まります．(論理がだいぶ怪しい．)

##方針2: 主成分の線型結合でデータが表されるとする(行列分解)
　方針2ではi番目の観測点$x_i$が主成分の線型結合で表されるという考え方による定式化です(c.f.因子分析)．この仮定に則るならば，i番目の観測点$x_i$は

x_i = Lf_i + e_i

というモデルで表されます．ここで主成分得点$f_i$は直交するとします．つまり，

\begin{eqnarray}
\frac{1}{N}f_i^Tf_j=\left\{
\begin{array}{l}
1 &if\ i=j\\
0 &otherwise
\end{array}
\right.
\end{eqnarray}

を満たすとします．これをi番目での個体だけではなくX全体に対したモデルに書き直すと，

X = FL^T + E

これを最小二乗法によって最適化することを考えます．損失関数は

LS(F,L) = ||E||_F^2=||X-FL^T||_F^2

であり，これを$F^TF=NI_m$という制約のもとで最小化します．この問題はEckart & Young(1936)の定理によって，Xの特異値分解(Singular Value Decomposition, SVD)によって解くことができます．Xの特異値分解を

X = U\Lambda V^T

とすると，Xの低ランク近似行列$X_{low}$は

X_{low} = U_m\Lambda_m V_m^T (= FL')

で与えられ，$rank(X_{low})=m$を満たします．ここで，$\Lambda_m$はXのm番目の特異値までを体格成分とする対角行列で$U_m$,$V_m$それに対応する特異ベクトルを含む行列です．詳しくは，特異値分解(wiki)をみてください．これを用いて，FとLの解は

\begin{eqnarray}
F &=& \sqrt{N}U_m\\
L &=& \frac{1}{\sqrt{N}}V_m\Lambda_m
\end{eqnarray}

で与えられます．ここで，Hは任意の正則行列です(これのせいで負荷量の回転などの話が出てくる!!)．このモデルの詳しい話は後日時間ができたときに再投稿します．
#申し訳程度のコード
　本当に申し訳程度です．実行結果とか見れるのでjupyter notebookで残したほうがいいかなとは思ったのですが，用意するのがめんどくさすぎました．上で紹介した2つの方針のpcaの関数を書きました(固有値分解，特異値分解するだけ)．低ランク近似できているかと直交性が満たされているかの確認はやってます．

import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns 
import pandas as pd 

#使用した散布図
mu = np.array([1.5,-2]);sigma = np.array([[3,2],[2,4]])
ransu = np.random.multivariate_normal(mu, sigma,3000)
ransu_df = pd.DataFrame(ransu).rename(columns={0:"x",1:"y"})
sns.jointplot(x="x",y="y",data=ransu_df,color=".1")
plt.show()

#申し訳主成分分析の関数
def pca(data,ndim,alpha=0.5,method="decomp"):
	"""
	input: data, ndim, alpha, method
		data: data matrix
		ndim: 低ランク近似するときの次元数
		alpha: 方針2のパラメータ
		method: "orthTrans"は方針1(直交変換, orthogonal transformation) 
				"decomp"は方針2(行列分解, matrix decomposition)
	output: (F,L) or (XW,W)
		(F,L): "decomp"による結果
		(XW,W): "orthTrans"による結果
	"""
	data = data.astype("float64");n,p = data.shape
	if method == "decomp":
		U,lam,V = np.linalg.svd(data,full_matrices=False)
		F = np.sqrt(n)*U[:,:ndim]
		L = np.dot(V[:ndim,:].T,np.diag(lam[:ndim]))/np.sqrt(n)
		return F,L
	if method == "orthTrans":
		S = np.cov(data.T)
		eig_vals,W = np.linalg.eig(S)
		return np.dot(data,W[:,:ndim]), W[:,:ndim]


if __name__ == "__main__":
	mu2 = np.array([1,-1,4.5,-3,1])
	sigma2 = np.array([[1,2.1,2,3.7,3],[2.1,3,-7,-8,1.2],[2,-7,8,2.9,-1.7],[3.7,-8,2.9,11,0.2],[3,1.2,-1.7,0.2,5]])

	ransu2 = np.random.multivariate_normal(mu2,sigma2,3000)
	df_ransu2 = pd.DataFrame(ransu2)
	sns.pairplot(df_ransu2);plt.show()

	#方針2(行列分解)
	F,L = pca(ransu2,ndim=2,method="decomp")
	print("F\n",F)
	print("L\n",L)
	##低ランク近似の確認
	print("rank of X_low: ",np.linalg.matrix_rank(np.dot(F,L.T))) # rank(X_low) = rank(FL') = ndimとなっているかの確認
	#直交性の確認
	print("F'F = \n",np.dot(F.T,F)/3000)

	#方針1(データの直交変換)
	XW ,W = pca(ransu2,ndim=2,method="orthTrans")
	print("XW\n",XW)
	print("W\n",W)
	#低ランク近似の確認
	print("rank of X_low: ",np.linalg.matrix_rank(np.dot(XW,W.T))) # rank(X_low) = rank(XWW') = ndimとなっているかの確認
	#Wが列直交行列であることの確認
	print("W'W = \n",np.dot(W.T,W))

#終わりに
　この記事は私の勉強(しかも2年くらい前)の整理のために作成しました．書いているうちにわけわからなくなった部分がわんさか出てきたので，解決次第更新します．
#####以降の更新のキーワード

• Eckart and Young(1936)の定理
• 主成分分析(方針2)
  • ↑の解析的回転の話
  • スパース主成分分析
  • ロバスト主成分分析
• 因子分析(たっぷり)
• MDS
• K-meansクラスタリング(多分次これ)
• 独立成分分析
• Sutton and Barto(2014). _Reinforcement Learning: An Introduction_の訳
• 重回帰分析
• 決定木
• SVM,カーネル法