簡単な貪欲法を解いてみた

1.要約

　最適化は様々な手法を用いて，ある問題に対して，考えうる中で最も良い解を求める分野です．最適化の手法の中でも貪欲法(greedy algorithm)は，問題設定の中で考えられる解すべて*を検討しその中で最適な結果を与えるものを解として選択する手法です．パターンを全部検討すれば一番いいものもその中に含まれているでしょ？っていう考え方です．そうです，力技です．本記事は，競技プログラミングの練習問題(B - Addition and Multiplication)を解いた際に考えたことのメモとして書いています．

2.貪欲法

2.1 貪欲法って？

　貪欲法は，最適化の場面で頻繁に利用される手法です．wikipediaでは以下のように説明されています．

貪欲法は局所探索法と並んで近似アルゴリズムの最も基本的な考え方の一つである。
このアルゴリズムは問題の要素を複数の部分問題に分割し、それぞれを独立に評価を行い、評価値の高い順に取り込んでいくことで解を得るという方法である。動的計画法と異なり保持する状態は常に一つであり、一度選択した要素を再考する事は無い。このため得られる解は最適解であるという保証は無いが部分問題の解法と単純なソートのみでプログラムを実装することが可能であり、多く問題に対して多項式時間での近似アルゴリズムとなる。

後半，「動的計画法(Dynamic Programing, DP)と異なりムニャムニャ」と書かれていますが，大事なのは，

1. 問題を複数の部分問題に分割する
2. 各部分問題に対する解を評価する(各部分問題ごとに考えられる解のパターンは複数ある．)
3. 評価が最も良いものをその部分問題の解(=局所最適解)として，次の部分問題の解(これも複数通り考えられる)を評価する

の部分です．問題を部分問題に分割して，各部分問題に対する局所最適解を求めることを繰り返すという手法みたいですね．以下に，私の大まかなイメージを書いています．ある問題$Q$が存在して，それは$q_1,q_2,\cdots,q_m$の部分問題に分割されるとし，それぞれの問題に対する局所最適解を$s_{1},\cdots,s_{m}$と表すとします．
元々の問題$Q$(難しい)の解$S_Q$を求めるために，部分問題(易しい)を経由してたどり着いています．

2.2 問題設定

　AtCoderのB - Addition and Multiplicationを例として用います．

問題
square1001 は、電光掲示板に整数1が表示されているのを見ました。
彼は、電光掲示板に対して、以下の操作 A, 操作 B をすることができます。
操作 A： 電光掲示板に表示する整数を「今の電光掲示板の整数を2倍にしたもの」に変える。
操作 B： 電光掲示板に表示する整数を「今の電光掲示板の整数にKを足したもの」に変える。
square1001は、操作A,操作B合計でN回行わなければなりません。そのとき、N回の操作後の、電光掲示板に書かれている整数として考えられる最小の値を求めなさい。
制約

• $1\le N,K\le 10$
• 入力($N,K$)はすべて整数である

例えば$(4,3)$という入力が与えられた場合，出力は10です．$(10,10)$という入力が与えられた場合は，出力は76です．このような問題設定では，N回の操作のうち，それぞれで小さくなるものを選ぶという問題に分割できます．いくつかの具体例を樹形図で表してみます．上に向かう矢印が操作A(2倍する)，下に向かう矢印が操作B(K加える)を表し，赤丸が局所最適解を表しています．

• ケース1.入力が(4,3)の時

　操作の手順としては，A,A,B,Bであることがわかります．各ステップで考えられる次の値の大きい方に進むというのを繰り返しています．

• ケース2.入力が(4,1)の時

　部分問題の２つめで考えられる解が一致するケースです．今回はこういった場合，操作Aをするように設定しました．操作Bをするように設定しても同じ解にたどり着きます．(気になる方はご自分で書いてみてください)
* ケース3.入力が(5,6)の時

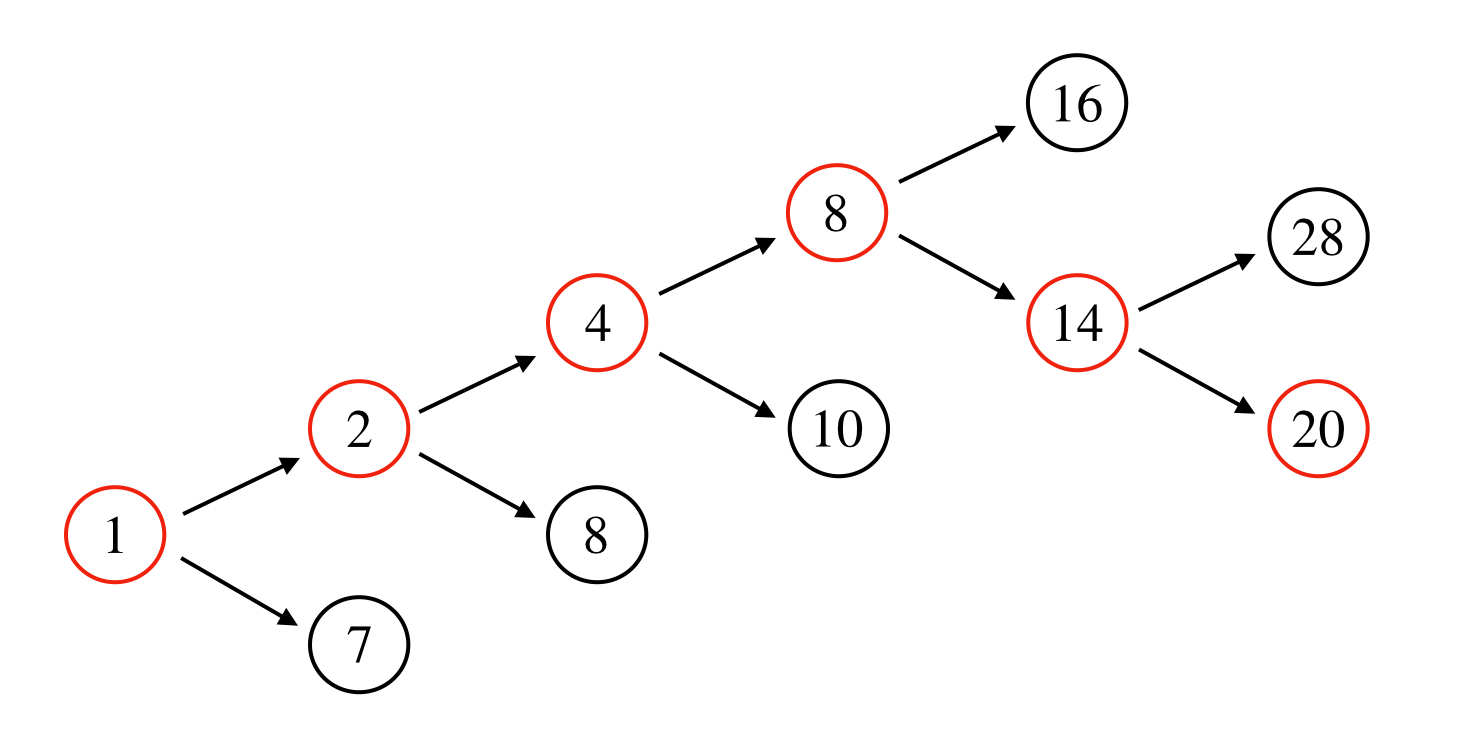
　操作の手順としては，A,A,A,B,Bという順番になることがわかります．Kが2以上の場合は，一つ目の部分問題の解は操作Aの方が選択されるという法則がわかります．これを一般化すると，操作Aをn回繰り返した際の解は$2^n$で，$2^n-2^{n-1} > K$となるまで操作Aを繰り返し，$2^n-2^{n-1} > K$となってからは残りの試行全てで操作Bを行えば良いということがわかります．(私は最初これで実装しようとしました．難しく考えすぎですね．)

3.Sample code

　今回は，競技プログラミングということで，c++で記述しています．

c++, addition_multiplication.cpp

#include<bits/stdc++.h>
using namespace std;

int main(){
    int N,K,num=1;
    cin >> N >> K;

    for(int i = 0; i < N; i++){
        if(num*2 <= num + K){
            num *= 2;
        }
        else{
            num += K;
        }       
    }
    cout << num << endl;
}

感想(読む必要ないです．自分用)

　久しぶりにc++を触って書き方を忘れていたので，現在AtCoderの簡単な練習問題を解いていますが，アホな私にちょうど良い難易度で楽しんでやれています．今回のように解法がパッと思いつかない問題は，中学校の数学の問題を解くように，易しめの具体例を手元で書きながら動作を確認していく作業が有効でした．考えて思いついた解法が解説の考え方と一致してたのは嬉しい(フフン)．
　c++もpython同様，機械学習のアルゴリズム実装に用いるのが目標なので，競技プログラミングの高度な問題をやるよりは，Eigenなどのライブラリ？の使い方に熟達した方がいいと思いました．