1. 雑要約
本記事では大数の弱法則,中心極限定理の様子をpythonで記述し実感することを目的としました.例のごとく稲垣先生の「数理統計学」を参考にしています.
2. 大数の弱法則
2-1.大数の弱法則とは
大数の弱法則とは,$X_1,\cdot,X_n$が独立で同一分布に従い,その平均と分散がが存在し,それぞれ$\mu$,$\sigma$であるとき,任意の正数$\epsilon$に対して$$\lim_{n \to \infty}P[|\bar{X_n}-\mu|\ge\epsilon]=0$$となる法則のことです.日本語で書くと,標本平均と母平均の差($=|\bar{X_n}-\mu|$)がある正数$\epsilon$より大きくなる確率は,サンプル数nが無限大に近くにつれて0になるというものです.ここでポイントとなるのは,分布の具体的な形を決めていない(=母平均,母分散のみ決めいている)という点です.
~証明~
チェビシェフの不等式から,$$P[|\bar{X_n}-\mu|\ge\epsilon]\le\frac{\sigma^2}{\epsilon^2 n}$$であり,
\begin{eqnarray}
\lim_{n \to \infty}P[|\bar{X_n}-\mu|\ge\epsilon]&\le&\lim_{n\to \infty}\frac{\sigma^2}{\epsilon^2 n}\\
=0
\end{eqnarray}
よって$\lim_{n \to \infty}P[|\bar{X_n}-\mu|\ge\epsilon]\le0$となるが,確率は非負なので等号が成立します.(証明終了)
(稲垣「数理統計学」p.101を参考に)
2-2. 実際に計算させてみた
とはいっても本当かなぁ?となったので,実際に計算してみることにしました.正規分布$N(0,10^2)$,$N(0,20^2)$,二項分布$Bin(1000,0.2)$($\mu=1000*0.2=200$),指数分布$Exp(6)$($\mu=1/6$)について計算してみました.
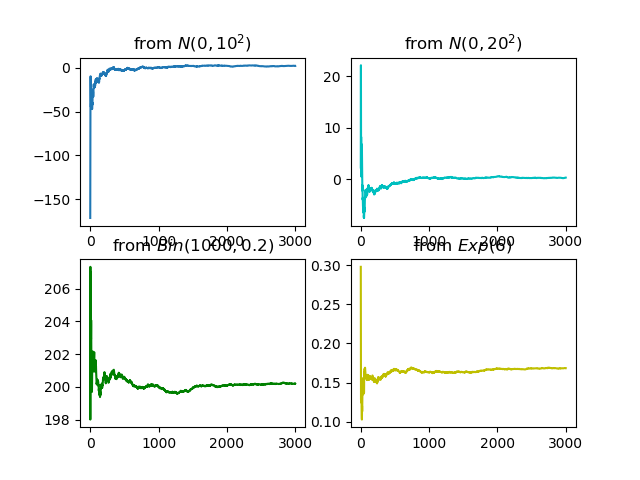
こう見てみるとやはりサンプル数nを増やすにつれて,標本平均が母平均にどんどん近づいていく様子が読み取れます(from Bin(1000,0.2)とfrom Exp(6)のあたりがぐしゃぐしゃですがそこはご愛嬌で).
3. 中心極限定理
3-1. 中心極限定理とは
中心極限定理とは,平均,分散がそれぞれ$\mu$,$\sigma^2$である分布からの無作為標本の標本平均$\bar{X_n}$を標準化した構成された確率変数$Z_n$の分布は標準正規分布($N(0,1)$)に分布収束する.つまり,$$\lim_{n\to\infty}P(Z_n\le z)=\Phi(z)=\int_{-\infty}^z\frac{1}{\sqrt{2\pi}}e^{-\frac{u^2}{2}}du$$が成り立つという定理のことです.ここで$\Phi(z)$は$Z_n$の分布関数を表しています.これも日本語で書くと,Z変換(標準化した)した確率変数は標本数が増えると,標準正規分布に従う確率変数の振る舞いに近づくということを表しています.分布収束という確率論の言葉が出ましたが,深くは掘り下げません.この定理のポイントは先ほどの大数の弱法則と同様,__Xの具体的な分布の形状にとらわれない__という点です.大数の弱法則と中心極限定理めちゃくちゃ大事です.酸素くらい大事.
~証明~
証明はめちゃ長くて書くのが面倒だったので,稲垣「数理統計学」p.102-104を見てください.3次の絶対モーメントの存在を仮定しているので割と簡潔で分かりやすい証明となっています.
3-2. 実際にやってみた
とはいえ,やっぱり本当かなぁ?と納得いかないので実際に可視化してみました.一様分布U(0,1)から標本数nを1,10,100,1000とした場合の度数分布をシミュレーションしています.黒い曲線は標準正規分布の確率密度関数を表しています.
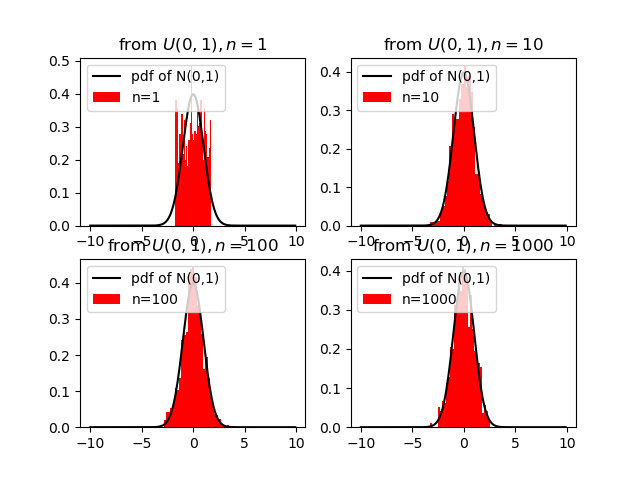
標本数を増やしていくにつれて,標準正規分布N(0,1)の形状に近づいていっていることが体感できました.他の分布(e.g.,二項分布,ポアソン分布,etc.)からの標本でも同様の振る舞いを観測できます.サンプルコードの分布の部分と平均,標準偏差の部分を書き換えればシミュレートできます.
4. サンプルコード
2秒で思いついたコード&無駄削減してない(動作確認だけしました)なので汚いコードですが,もしよかったら使ってください.
# -*- coding: utf8 -*-
import numpy as np
import random
import matplotlib.pyplot as plt
import scipy.stats as sp
## 大数の法則
### 1-1. 正規分布 N(0,100)
rv_list = []; mean_list = []
for i in range(3000):
a = random.gauss(mu=0, sigma=100)
rv_list.append(a)
mean_list.append(np.mean(rv_list))
plt.subplot(2,2,1)
plt.plot(np.arange(len(mean_list)),mean_list)
plt.title("from $N(0,10^2)$")
### 1-2. 正規分布 N(0, 20^2) numpy.random.normal()を使って
rv_list = []; mean_list = []
for i in range(3000):
a = np.random.normal(0, 20, 1)
rv_list.append(a)
mean_list.append(np.mean(rv_list))
plt.subplot(2,2,2)
plt.plot(np.arange(len(mean_list)),mean_list,color="c")
plt.title("from $N(0,20^2)$")
### 2. 二項分布 Bin(1000,0.2) mu=1000*0.2=200
rv_list = []; mean_list = []
for i in range(3000):
a = np.random.binomial(1000, 0.2, 1)
rv_list.append(a)
mean_list.append(np.mean(rv_list))
plt.subplot(2,2,3)
plt.plot(np.arange(len(mean_list)),mean_list,color="g")
plt.title("from $Bin(1000,0.2)$")
### 3. 指数分布 Exp(6), mu=1/6(だいたい0.167)
rv_list = []; mean_list = []
for i in range(3000):
a = np.random.exponential(1/6, size=1)
rv_list.append(a)
mean_list.append(np.mean(rv_list))
plt.subplot(2,2,4)
plt.plot(np.arange(len(mean_list)),mean_list,color="y")
plt.title("from $Exp(6)$")
# plt.savefig("適当なディレクトリ")
plt.show()
## 中心極限定理
x_range = np.arange(-10,10,0.1)
gauss = sp.norm.pdf(x_range,0,1)
### 1 一様分布 U(0,1), mu = (0+1)/2 = 1/2, sigma^2 = (1-0)^2/12 = 1/12
mu = 1/2;sigma = np.sqrt(1/12)
z1_l = [];z10_l = [];z100_l = [];z1000_l = []
for i in range(1000):
a1 = np.random.uniform(size=1)
z1_l.append(np.sqrt(1)*(np.mean(a1)-mu)/sigma)
a10 = np.random.uniform(size=10)
z10_l.append(np.sqrt(10)*(np.mean(a10)-mu)/sigma)
a100 = np.random.uniform(size=100)
z100_l.append(np.sqrt(100)*(np.mean(a100)-mu)/sigma)
a1000 = np.random.uniform(size=1000)
z1000_l.append(np.sqrt(1000)*(np.mean(a1000)-mu)/sigma)
plt.subplot(2,2,1)
plt.hist(z1_l,bins=30,color="r",normed=True,label="n=1")
plt.plot(x_range,gauss,color="black",label="pdf of N(0,1)")
plt.legend(loc="upper left")
plt.title("from $U(0,1),n=1$")
plt.subplot(2,2,2)
plt.hist(z10_l,bins=30,color="r",normed=True,label="n=10")
plt.plot(x_range,gauss,color="black",label="pdf of N(0,1)")
plt.legend(loc="upper left")
plt.title("from $U(0,1),n=10$")
plt.subplot(2,2,3)
plt.hist(z100_l,bins=30,color="r",normed=True,label="n=100")
plt.plot(x_range,gauss,color="black",label="pdf of N(0,1)")
plt.legend(loc="upper left")
plt.title("from $U(0,1),n=100$")
plt.subplot(2,2,4)
plt.hist(z1000_l,bins=30,color="r",normed=True,label="n=1000")
plt.plot(x_range,gauss,color="black",label="pdf of N(0,1)")
plt.legend(loc="upper left")
plt.title("from $U(0,1),n=1000$")
# plt.savefig("適当なディレクトリ")
plt.show()