1. 要約
本記事では,カテゴリカルデータの数量化の際に利用される多重対応分析についてまとめました.多重対応分析は,カテゴリカルデータからカテゴリー座標値を求める手法です.パラメータ推定では,特異値分解が重要な役割を果たします.記事の後半では,Rでの実装例を載せています.
数量化いいですよね.最近面白いなと思ってます.(研究対象とできるかは別として.というか,こんなんやってる場合じゃねえ!!)
2. 多重対応分析
2.1 どんな手法?
以下のようなデータを考えます.
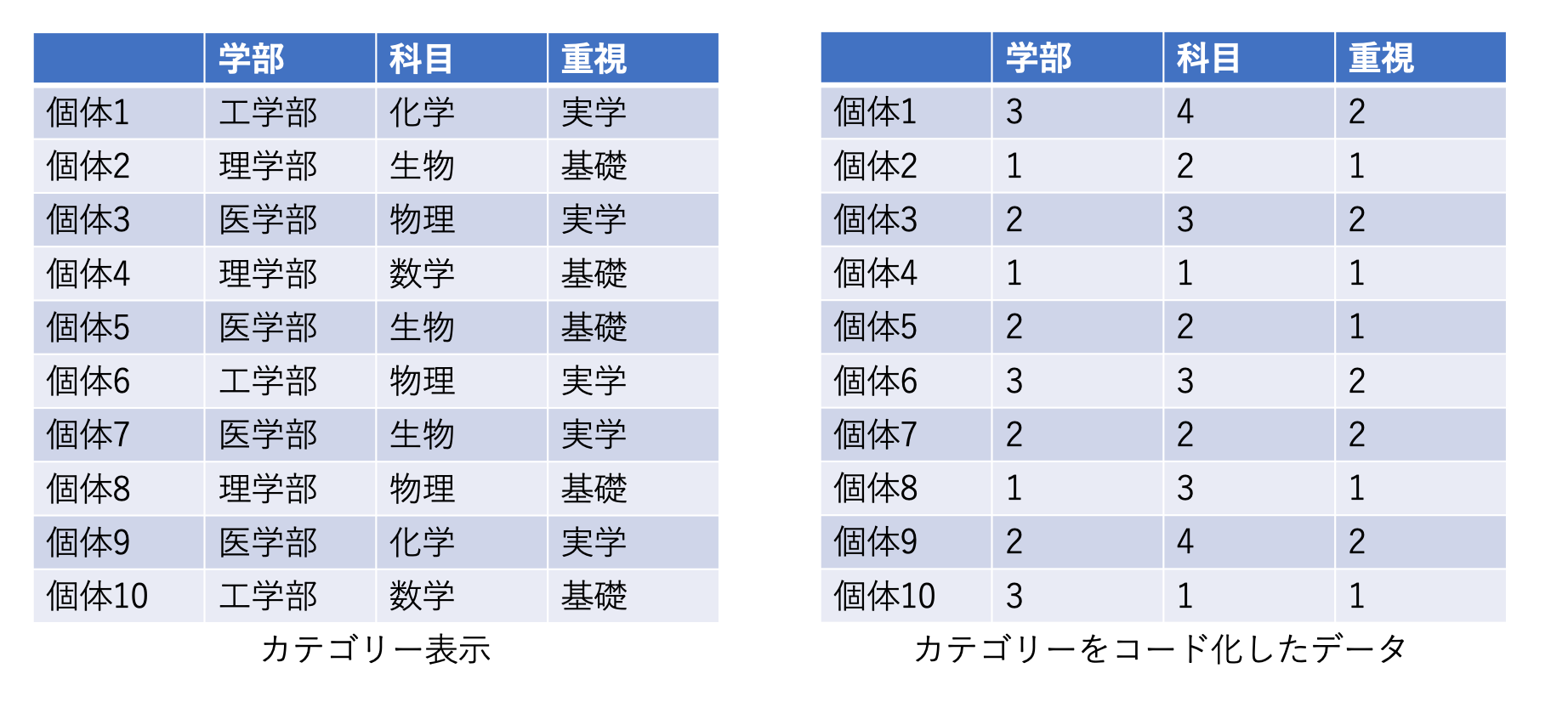
左が,個体の属性値をカテゴリー表示でまとめた表で,右が,学部変数では「1=理学部,2=医学部,3=工学部」,科目変数では「1=数学,2=生物,3=物理,4=化学」,重視変数では「1=基礎,2=重視」のようにカテゴリーをコード化したものをまとめた表です.多重対応分析は,このようなデータからカテゴリーの座標値を計算することを目的とします.カテゴリーの座標値が求まったならば,以下のような散布図を描画でき,カテゴリー間の関係を視覚的に把握することができます.
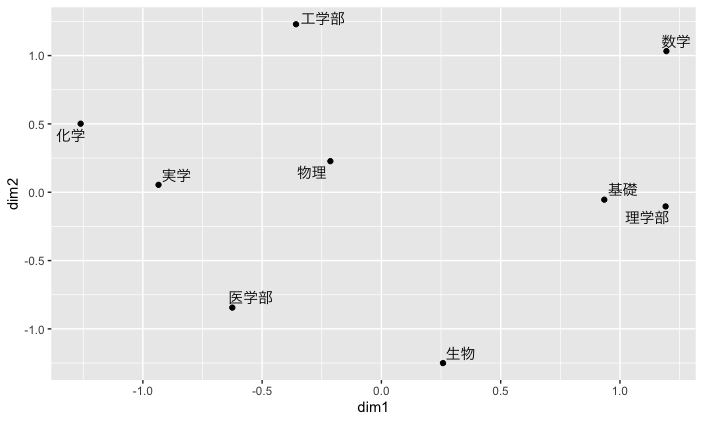
この散布図から,例えば,理学部と基礎,物理と実学が近接していることがわかり,理学部の学生は基礎を重視しており,物理は基礎よりも実学寄りの学問であると判断できます.変数(データの列)毎に線で結んだ図は以下のようになります.
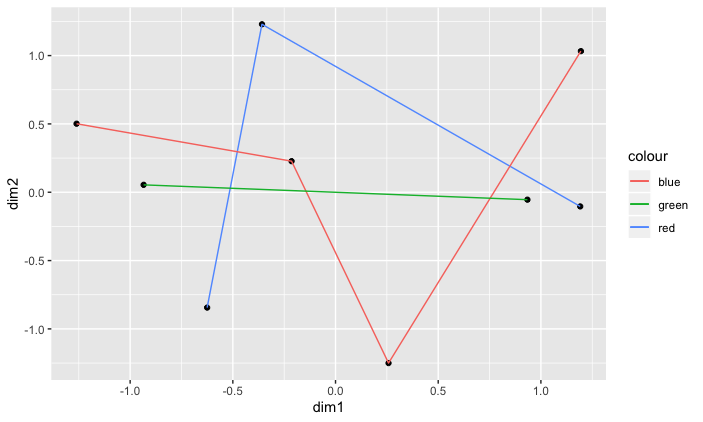
(本当は,二つの図を重ねて一つの図として表示したかったのですが,うまくいかなかったです.悔しい!)
2.2 定式化
今回は,等質性基準の最適化による定式化をまとめます.等質性基準とは,「各個体の主成分得点と,その個体が該当するカテゴリーの座標値は近い,すなわち,等質的な値をとる」(足立・村上, 2011)という等質性仮定のもとで,最小化される基準です.個体iの得点ベクトルを$f_i$,変数jにおける個体iの該当カテゴリーの得点を$w_{jx_{ij}}$とすると,これらのずれは,
\begin{align}
e_{ij}^2 &= \|{\bf f}_{i} - \tilde{{\bf w}}_{jx_{ij}}\|^2\\
&= \|{\bf f}_{i} - \sum_{k=1}^{K_j} g_{ijk} {\bf w}_{jk}\|^2
\end{align}
という平方距離によって表されます.このずれが小さいほど,等質性仮定が満たされていると言えます.データ全体の等質性仮定からの逸脱度は
\begin{align}
LH(F,W) &= \sum_{i = 1}^N\sum_{j=1}^M e_{ij}^2 \\
&= \sum_{i = 1}^N\sum_{j=1}^M \|{\bf f}_{i} - \sum_{k=1}^{K_j} g_{ijk} {\bf w}_{jk}\|^2\\
&= \sum_{j = 1}^M \|F - G_jW_j\|^2_F
\end{align}
となります.多重対応分析は,この基準(Loss of Homogeneity, LH)を最小化する$F,W$を求めます.ただし,$G_j$は変数jのカテゴリーに属するかどうかを表すメンバーシップ行列を表します.$F=O_{n,p},W=O_{K_j,p}$という解を避けるために,
\begin{align}
JF &= F\\
\frac{1}{n} F'F &= I_p
\end{align}
という制約を課します.
3. 更新式の導出
損失関数は,以下のように展開されます.
\begin{align}
LH(F,W) &= \sum_{j = 1}^M(trW_j'G_j'G_jW_j - 2trW_j'G_j'F + trF'F)\\
&= trW'DW - 2trW'G'F + nmp
\end{align}
突然ですが,最適化するパラメータに関して,これと等価な損失関数
\begin{align}
g(F,W) &= \|GD^{-1/2} - \frac{1}{n}FW'D^{1/2}\|^2_F\tag{1}\\
(&= \|GD^{-1/2}\|^2_F - \frac{2}{n}trW'G'F + \frac{1}{n}trW'DW)
\end{align}
を考えます.これらを最小化する$F,W$は,$GD^{-1/2}$の特異値分解を
$$GD^{-1/2} = N\Phi M'$$
とすると,
\begin{align}
F &= \sqrt{n}N_pT\\
W &= \sqrt{n}M_p\Phi_p T
\end{align}
で与えられます.ここで,$T$は正規直交行列を表します.何故これでLHが最小化されるというと,$F,W,D$の行列のサイズから,$$rank(n^{-1}FW'D^{1/2}) \le p$$であるので,これらの制約条件のもとで$Y = n^{-1}FW'D^{1/2}$とした時の$(1)$の最小化は,
g(Y) = \|GD^{1/2} - Y\|^2_F
の最小化と等しくなります.これは,$GD^{1/2}$を階数が$p$の行列$Y$で近似する問題です.この低階数近似は,$Y$の特異値分解で達成されます.
4. 実装例
最近はpythonを封印して,授業でよく使うRを極めようとしています.目標はRでささっと実装,Rcppで書き換えて高速化というのを習熟することです.やはり慣れ大事.$T$は単位行列としています.回転は今回考慮していません.データは,参考書籍のデータを利用しています.
cate.to.memb = function(vec,nrow){
ele = unique(vec); mem = length(ele)
G = matrix(0,nrow,mem)
for(i in 1:nrow){
G[i,vec[i]] = 1
}
return(G)
}
mca.my = function(Cate,ndim){ #等質性基準(loss of homogenuity)
n = nrow(Cate);p = ncol(Cate)
G = NULL
size = NULL
for(ii in 1:p){
G.ele = cate.to.memb(Cate[,ii],n)
size = c(size,ncol(G.ele))
G = cbind(G,G.ele)
}
D.sqrt = diag(1/(diag(t(G)%*%G))^(1/2))
J = diag(n) - (1/n)*matrix(1,n,n)
JGD = J%*%G%*%D.sqrt
svd = svd(JGD)
F = svd$u[,1:ndim] * sqrt(n)
W = D.sqrt %*% svd$v[,1:ndim] %*% diag(svd$d[1:ndim]) * sqrt(n)
return(list(G = G, F = F, W = W, G1W1 = G[,1:3]%*%W[1:3,]))
}
subjects = read.csv("適当なパス/subject_a_m.csv")
#多重対応分析の実行
res = mca.my(subjects,2)
#カテゴリー座標値のdataframe化
W = res$W
rownames(W) = c("理学部", "医学部", "工学部", "数学",
"生物", "物理", "化学", "基礎", "実学")
df.W = data.frame(dim1 = W[,1], dim2 = W[,2])
#列毎のデータフレーム
df.W1 = df.W[1:3,]
df.W2 = df.W[4:7,]
df.W3 = df.W[8:9,]
#可視化
library(ggplot2)
library(ggrepel)
#カテゴリーの名前付き
g = ggplot(NULL) +
geom_point(data = df.W, aes(x = dim1, y = dim2, label = rownames(df.W))) +
geom_line(data = df.W1, aes(x = dim1, y = dim2, color = "red")) +
geom_line(data = df.W2, aes(x = dim1, y = dim2, color = "blue")) +
geom_line(data = df.W3, aes(x = dim1, y = dim2, color = "green")) +
geom_text_repel(family = "HiraKakuProN-W3")
plot(g)
#質問項目ごとに線で結ぶ
g2 = ggplot(data = df.W, aes(x = dim1, y = dim2, label = rownames(df.W))) +
geom_point() +
geom_text_repel(family = "HiraKakuProN-W3")
plot(g2)
参考文献
足立・村上(2011). 非計量多変量解析法-主成分分析から多重対応分析へ-amazon