1. 雑要約
本記事では分散分析が何をやっててどうしてあの統計量を利用するのかという点を取り扱っています.各所で現れる図表はpythonの出力(+keynote)で書いているので一応コードも載せています.いつも通り稲垣「数理統計学」等を利用しました.
また,この記事は私の勉強のメモなのでミスなどを発見された場合は教えてください.
2. 問題例: そいつらの分布の母平均は本当に一致してる?
例1. 所得と都市の規模
都市規模が500万都市,100万都市,50万都市,10万都市のそれぞれからサラリーマンの所得の標本を抽出するとする.ここで一元配置分散分析では,それぞれの母平均は一致してるか?つまり,都市の規模でサラリーマンの所得の平均に差があるかを考える問題となる.(稲垣「数理統計学」p.240から)
例2. 湖の各地点での汚染度
水の中に含まれる酸素用改良は水質汚染を示す指標の1つである(酸素用改良が少ないほど汚染が進んでいる).ある湖の4地点において取られた無作為標本の酸素溶解量について,4地点における酸素溶解量に有意差があるか検定せよ.(稲垣「数理統計学」p.243 例題13.1)
例3. 織物の樹脂濃度
織物の樹脂加工工程で,樹脂濃度(A)が織物の引っ張り強さに与える影響を調べるため,それを4水準にとって実験し,下記のデータを得た.これを分析せよ.また各水準の平均に95%信頼区間を付したグラフを作成せよ.
| 温度 | $A_1$ | $A_2$ | $A_3$ | $A_4$ |
|---|---|---|---|---|
| デ | 70 | 74 | 78 | 76 |
| l | 73 | 74 | 75 | 78 |
| タ | 75 | 77 | 79 | 75 |
| (kg) | 72 | 75 | 80 | 75 |
(東京大学出版会「自然科学の統計学」p.109 練習問題3.2)
(あとで,この問題を4.分散分析を実際にやってみるで解きます.)
3. 分散分析のフレームワーク
3-1. どんなケースで使う?
まずはどのようなケースで分散分析を適応できるかについて考えます.先ほどの3つの例を見て共通している点は,__比較を行うのが複数($\ge$3)の群である__という点です.例えば1群ならばz検定やt検定を行えば良いし,2群の場合は2標本問題を行えば良いです.群の数がそれ以上になると,群の考えうるすべてのペアに対して検定を行うこともできますが,__有意水準の扱い__が難しくなることと,効率的でないという点から(?),一般的には分散分析を行うことが多いです.
3-2. グラフィカルにやってることをおおまかに掴む
分散分析は,「各群(r群あるとします)の毋平均が一致している」というのを帰無仮説,「いやいやそんなことはないでしょ〜」というのを対立仮説として検定を行います.整理すると以下のように書けます.
\begin{eqnarray}
\left\{\begin{array}
a H_0: \mu_1=\mu_2=\cdots=\mu_r\\
H_1: \mbox{上記以外}
\end{array}\right.
\end{eqnarray}
以下の図は群が3つあるとした時の母集団分布(実際には未知)と総平均(=全標本の平均)を視覚化したものです.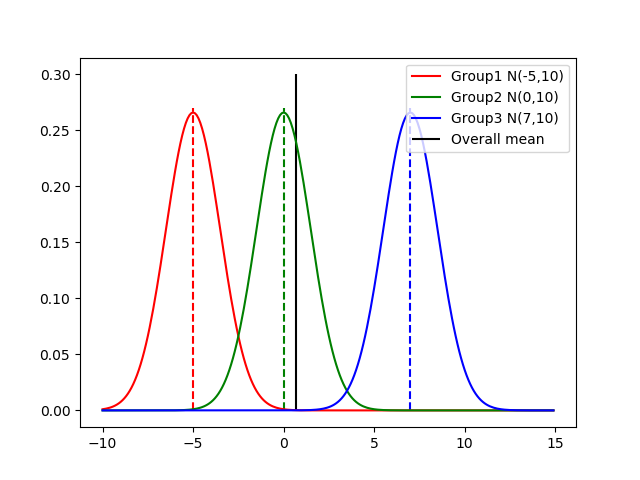
Group i (i=1,2,3)が群,Overall meanが総平均を表しています.帰無仮説が正しいとき,各群の母平均は総平均に近づきます(ほんとは__$H_0$が正しいときの各群の母平均の位置は総平均の位置に一致します__).イメージは以下のようなものです.
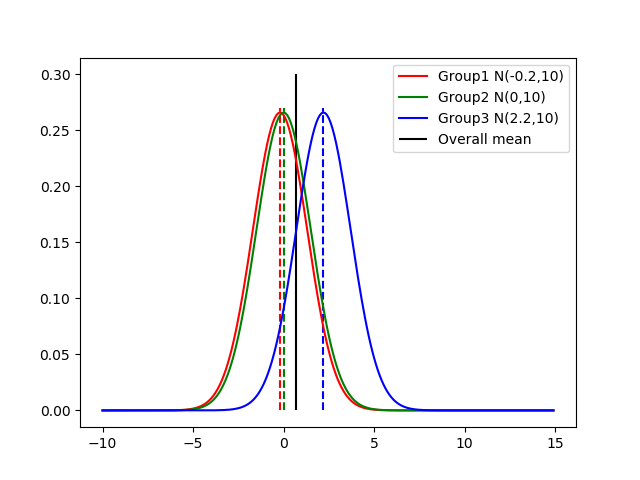
分散分析では,各群の母集団が__1枚目のような位置か,2枚目のような位置かどっちなんだい?__というのを検定しています.
では,次に以上のような挙動を検定統計量として表現することを考えます.標本から計算された総平均からの散らばり(=総変動$S_T$)を
\begin{eqnarray}
S_T=\sum_{i=1}^r\sum_{j=1}^{n_i}(y_{ij}-\bar{y})^2
\end{eqnarray}
とします.ここで$\bar{y}_{..}$は標本から計算した総平均を表しています.これだけだと各群の平均の情報がないので,各群の標本平均を挟み込みます.
\begin{eqnarray}
S_T&=&\sum_{i=1}^r\sum_{j=1}^{n_i}(y_{ij}-\bar{y})^2\\
&=&\sum_{i=1}^r\sum_{j=1}^{n_i}(y_{ij}-\bar{y}_{i.}+\bar{y}_{i.}-\bar{y})^2\\
&=&\sum_{i=1}^r\sum_{j=1}^{n_i}(y_{ij}-\bar{y}_{i.})^2+\sum_{i=1}^rn_i(\bar{y}_{i.}-\bar{y})^2\\
&&(S_w:=\sum_{i=1}^r\sum_{j=1}^{n_i}(y_{ij}-\bar{y}_{i.})^2,S_b:=\sum_{i=1}^rn_i(\bar{y}_{i.}-\bar{y})^2)\\
&=&S_w+S_b
\end{eqnarray}
総変動$S_T$に各群の平均を挟み込むことで,総変動は各群の平均からの標本の散らばりを表す$S_w$(級内変動)と総平均からの各群の標本平均の散らばりを表す$S_b$(級間変動)に分割することができました.$S_w,S_b$はそれぞれ自由度n-r,r-1のχ二乗分布に従います.分散分析では,これらの比
\begin{eqnarray}
\frac{\frac{S_b}{r-1}}{\frac{S_w}{n-r}} \sim F_{n-r}^{r-1}
\end{eqnarray}
を検定統計量として用います.先ほどの図に総変動などを書き込んだものが以下の図です.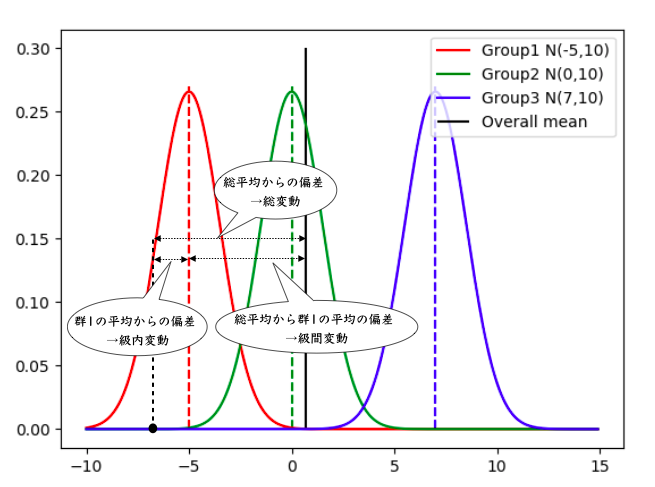
もし帰無仮説$H_0=\mu_1=\cdots=\mu_r$が間違っているとすると,級間変動が大きくなるので,結果として検定統計量の値も大きくなります.従って帰無仮説は棄却されやすくなります.実際に分散分析を行う場合は,次の章のように分散分析表を作成して検定を行います.
4. 分散分析表を使って実際にやってみる
分散分析表は以下のような表を指します.
| 平方和 | 自由度 | 平均平方和 | F値 | |
|---|---|---|---|---|
| 級間 | $S_b=\sum n_i(\bar{y}_{i.}-\bar{y})^2$ | $r-1$ | $\frac{\sum n_i(\bar{y}_{i.}-\bar{y})^2}{r-1}$ | |
| 級内 | $S_w=\sum\sum(y_{ij}-\bar{y}_{i.})^2$ | $n-r$ | $\frac{\sum\sum(y_{ij}-\bar{y}_{i.})^2}{n-r}$ | $F=\frac{\frac{S_b}{r-1}}{\frac{S_w}{n-r}} \sim F_{n-r}^{r-1}$ |
| 総 | $S_T=\sum\sum(y_{ij}-\bar{y})^2$ | $n-1$ | ||
| 例3の織物の樹脂濃度に対して,分散分析表を作成すると, |
| 平方和 | 自由度 | 平均平方和 | F値 | |
|---|---|---|---|---|
| 級間 | $62.75$ | $3$ | $20.92$ | |
| 級内 | $39.00$ | $13$ | $3.25$ | $F=6.44$ |
| 総 | $101.75$ | $15$ | ||
| となり,$F_{0.01}(3,13)=5.739$,$F_{0.005}(3,13)=6.926$から,有意水準1%では,母平均は軍によって異なるとは言えませんが,有意水準0.5%では$H_0$は棄却され,母平均に差があると言えます. |
感想(読み飛ばしてください)
なぜ今さら検定なんてものをやっているのか...自分でも謎です.勉強のモチベーションとしては統計検定で出題されている&授業の復習というのが大きいです.今回取り上げなかった交互作用(実験系ではこっちが大事そう)も機会があれば紹介します.
以下作図のために書いたコードです.
# -*- coding: utf-8 -*-
import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as sp
import matplotlib as mpl
# 1つ目の図表
x_range = np.arange(-10,15,0.1)
f1 = sp.norm.pdf(x_range,-5,1.5)
f2 = sp.norm.pdf(x_range,0,1.5)
f3 = sp.norm.pdf(x_range,7,1.5)
# mpl.rcParams['font.family'] = 'AppleGothic' #日本語をグラフに表示するための操作
plt.plot(x_range,f1,color="r",label="Group1 N(-5,10)")
plt.vlines([-5],0,0.27,"r",linestyle="dashed")
plt.plot(x_range,f2,color="g",label="Group2 N(0,10)")
plt.vlines([0],0,0.27,"g",linestyle="dashed")
plt.plot(x_range,f3,color="b",label="Group3 N(7,10)")
plt.vlines([7],0,0.27,"b",linestyle="dashed")
plt.vlines([2/3],0,0.3,"black",label="Overall mean")
plt.legend(loc="upper right")
# plt.savefig("")
plt.show()
# 2つ目の図表
x_range = np.arange(-10,15,0.1)
f1 = sp.norm.pdf(x_range,-0.2,1.5)
f2 = sp.norm.pdf(x_range,0,1.5)
f3 = sp.norm.pdf(x_range,2.2,1.5)
plt.plot(x_range,f1,color="r",label="Group1 N(-0.2,10)")
plt.vlines([-0.2],0,0.27,"r",linestyle="dashed")
plt.plot(x_range,f2,color="g",label="Group2 N(0,10)")
plt.vlines([0],0,0.27,"g",linestyle="dashed")
plt.plot(x_range,f3,color="b",label="Group3 N(2.2,10)")
plt.vlines([2.2],0,0.27,"b",linestyle="dashed")
plt.vlines([2/3],0,0.3,"black",label="Overall mean")
plt.legend(loc="upper right")
# plt.savefig("")
plt.show()