1. 要約

　本記事では，正準相関分析のプログラムを組むための解説記事です．自分の勉強メモとしての側面が強いので少し雑です．記事の最後にRで記述したサンプルコードを載せています．

2. 正準相関分析とは

　正準相関分析(Canonical Correlation Analysis, CCA)は，Hotelling(1936)にて開発された手法で，二つの変数群のそれぞれを混ぜ合わせ，最も相関が高くなるような変数を作成する手法である．ここで混ぜ合わされてできた変数は，正準変数(canonical variable)と呼ばれ，正準変数間の相関係数は，正準相関係数(canonical correlation)と呼ばれている．例えば，以下のように，

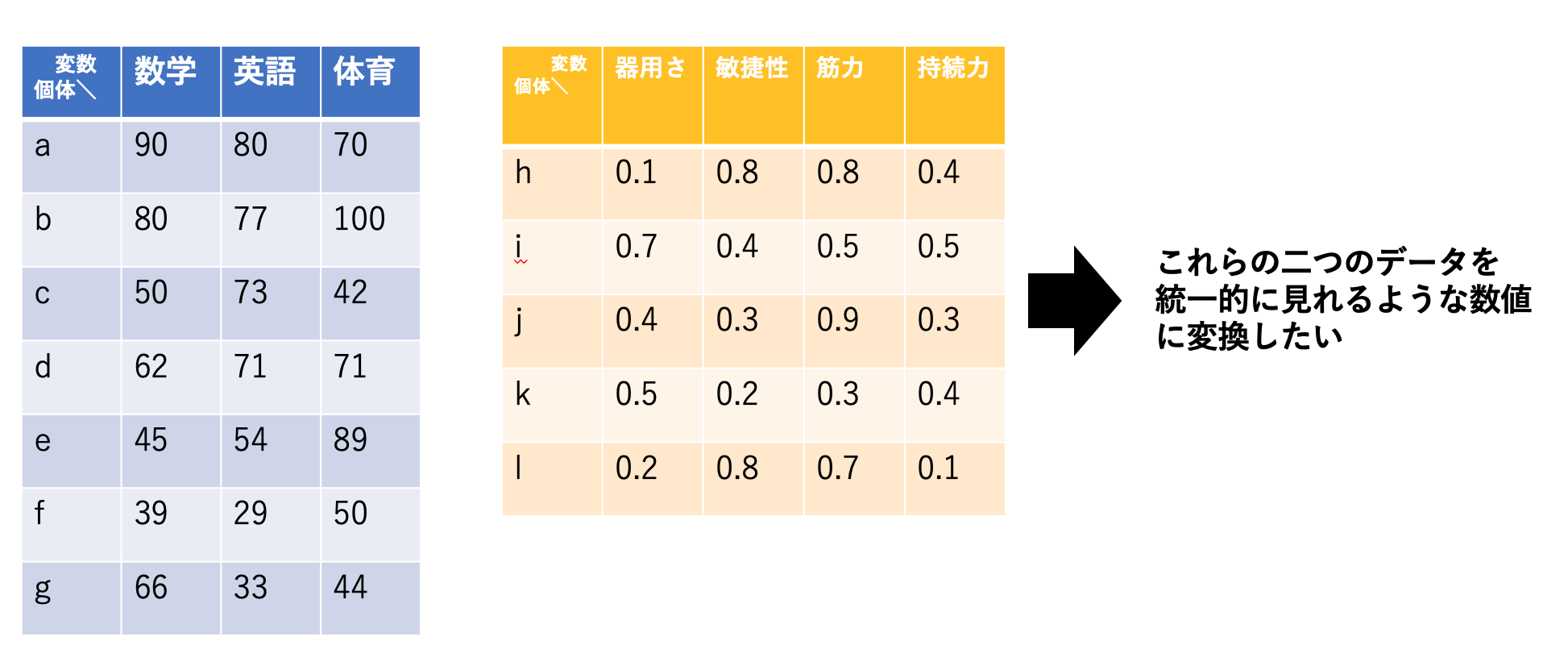
英語，数学，体育の成績の得点を持つグループと，運動能力について測定したグループのデータに対して，正準相関分析は適用される．イマイチ私には，どう使って良いのかはピンと来ていない．赤穂(2006)のように，信号データに対して適用している例もある．
　二つの群(行列)をそれらの相関が最大になるようなベクトルに変換して，統一的な指標を得る手法と考えると，他に応用できそうな気もする．

3. 一般の定式化

以下の表記を利用する．

$X_{rv} = (X_1,\ldots,X_p)^T$: 確率変数ベクトル
$Y_{rv} = (Y_1,\ldots,Y_q)^T$: 確率変数ベクトル
X: 群1のデータ行列($n\times p$)，行が個体，列が変数を表す．列中心化されているとする．
Y: 群2のデータ行列($n\times q$)，行が個体，列が変数を表す．列中心化されているとする．
A: 群1の変数を混ぜ合わせる行列($p\times m$)
B: 群2の変数を混ぜ合わせる行列($q\times m$)
$||\cdot||_F$: フロベニウスノルム．

　正準相関分析は，正準相関係数を最大化するような係数$a,b$を求める問題として定式化される．

\begin{eqnarray}
\underset{a,b}{maximize}\ &&Corr(a^TX_{rv},b^TY_{rv})\\
&=&\frac{Cov(a^TX_{rv},b^TY_{rv})}{\sqrt{V[a^TX_{rv}]}\sqrt{V[b^TY_{rv}]}}\\
&=& \frac{a^TCov(X_{rv},Y_{rv})b}{\sqrt{a^TV[X_{rv}]a}\sqrt{b^TV[Y_{rv}]b}}\\
&=& \frac{a^TC_{xy}b}{\sqrt{a^TV_{xx}a}\sqrt{b^TV_{yy}b}}\\
subject\ to\ && a^TV[X_{rv}]a = 1,\ b^TV[Y_{rv}]b = 1
\end{eqnarray}

この問題に対するラグランジュ関数は，$\lambda_x,\lambda_y \ge 0$を用いて
$$L(\lambda_x,\lambda_y,a,b) = a^TC_{xy}b - \frac{\lambda_x}{2}(a^TV_{xx}a-1) - \frac{\lambda_y}{2}(b^TV_{yy}b-1)$$
であり，a,bのそれぞれで偏微分したものを0と置いて，停留点を求めると，

\begin{eqnarray}
\frac{\partial L}{\partial a} &=& C_{xy}b - \lambda_x V_{xx}a = {\bf 0}\tag{1}\\
\frac{\partial L}{\partial b} &=& C_{xy}^Ta - \lambda_y V_{yy}b = {\bf 0}\tag{2}
\end{eqnarray}

さらに，一つ目の式，二つ目の式にそれぞれ，$a^T,b^T$をかけることで，

\begin{eqnarray}
0&=&a^TC_{xy}b - \lambda_x a^TV_{xx}a - b^TC_{xy}^Ta + \lambda_y b^TV_{yy}b\\
&=& \lambda_y b^TV_{yy}b - \lambda_x a^TV_{xx}a
\end{eqnarray}

となる．これと，制約式$b^TV_{yy}b=a^TV_{xx}a = 1$から，
$$\lambda_x = \lambda_y$$
である．以降これらをまとめて$\lambda$とおく．仮に$V_{yy}$が正則であるとすると，(2)式から，
$$b = \frac{V_{yy}^{-1}C_{xy}^Ta}{\lambda}$$
であり，これを(1)に代入すると，
$$C_{xy}V_{yy}^{-1}C_{xy}^Ta = \lambda^2 V_{xx}a$$
が得られる．これは，$Ax = \lambda Bx$の形であり，一般化固有値問題(generalized eigen problem)と呼ばれる．これのソルバーを持っているのなら，それを使えばいいのだが，もし持っていない場合は，これを通常の固有値問題に変換することが必要となる．$V_{xx}$が正定値対称行列であることに注目すると，コレスキー分解(Cholesky decomposition)が適用できる．$V_{xx}$のコレスキー分解を
$$V_{xx} = L_xL_x^T$$
とし，$a^* = L_{x}^Ta$のように変換すると，先ほどの一般化固有値問題は，

\begin{eqnarray}
&&C_{xy}V_{yy}^{-1}C_{xy}^T(L_{x}^T)^{-1}a^* = \lambda^2 L_{x}a^*\\
&\Leftrightarrow& L_{x}^{-1}C_{xy}V_{yy}^{-1}C_{xy}^T(L_{x}^T)^{-1}a^* = \lambda^2 a^*
\end{eqnarray}

のように通常の固有値問題に帰着される．この問題の解を$a^* = a_{ans}$とすると，正準相関係数$a$の解は，
$$\widehat{a} = (L_x^T)^{-1}a_{ans}$$
で表される．$b$も同様のステップで求められる．

4. 別の定式化(SVDを用いる)

正準相関分析は，以下の最小二乗法基準を最小化することでもパラメータを推定できる．

\begin{eqnarray}
\underset{A,B}{minimize}&&\|XA-YB\|_F^2 = tr(XA-YB)^T(XA-YB)\\
subject\ to\ &&\frac{1}{n}A^TX^TXA =I_m,\  \frac{1}{n}B^TY^TYB=I_m
\end{eqnarray}

この定式化のざっくりとしたイメージは，合成して出来た行列が似ている(=ダイバージェンスが小さい)と，正準相関係数も高いというものである．損失関数は，

\begin{eqnarray}
\|XA-YB\|_F^2 &=& tr(XA-YB)^T(XA-YB) \\
&=& tr(A^TX^TXA - A^TX^TYB + B^TY^TYB) \\
&=& tr(nI_m - A^TX^TYB + nI_m)\\
&=& 2nm - trA^TX^TYB
\end{eqnarray}

のように展開されることから，損失関数の最小化は，$trA^TX^TYB$の制約付き最大化問題に帰着する．ここで，

\begin{eqnarray}
A^TX^TYB &\propto& A^T(n^{-1}X^TY)B\\
&=& A^TC_{xy}B\\
&=& A^TV_{xx}^{1/2}V_{xx}^{-1/2}C_{xy}V_{yy}^{-1/2}V_{yy}^{1/2}B\\
&=& A^TV_{xx}^{1/2}R_{xy}V_{yy}^{1/2}B\\
&&(R_{xy} := V_{xx}^{-1/2}C_{xy}V_{yy}^{-1/2})\\
&=& A_*^TR_{xy}B_*\\
&&(A_*: = V_{xx}^{1/2}A,\ B_*:=V_{yy}^{1/2}B) 
\end{eqnarray}

であることから，一般的な正準相関分析の定式化に対応していることがわかる．
　制約を満たして，$trA_* ^TR_{xy}B_*$を最大化するA,Bは，特異値分解$$R_{xy} = KDL^T$$を用いて，

\begin{eqnarray}
A &=& V_{xx}^{-1/2}K_t\\
B &=& V_{yy}^{-1/2}L_t
\end{eqnarray}

と表される．ここでtは分析者があらかじめ設定する正準変数の個数である．また，特異値分解の結果の対角行列$D$の対角要素が正準相関係数である．

5. サンプルコード(R言語)

　特異値分解を用いる定式化のプログラムを書きました．データと一部コードはhttps://stats.idre.ucla.edu/r/dae/canonical-correlation-analysis/を参考にさせていただいています．参考にした部分は"="が"<-"になっています．

R,cca.R

CCA.my = function(X,Y,ndim){
  #suppose that nx = ny
  nx = nrow(X); ny = nrow(Y)
  px = ncol(X); py = ncol(Y)
  for(i in 1:px){
    X[,i] = X[,i] - mean(X[,i])
  }
  for(i in 1:py){
    Y[,i] = Y[,i] - mean(Y[,i])
  }
  Cxx = (1/nx) * t(X) %*% X
  Cyy = (1/ny) * t(Y) %*% Y
  Cxy = (1/nx) * t(X) %*% Y
  evd.Cxx = eigen(Cxx)
  Cxx.sqrt.inv = evd.Cxx$vectors %*% diag(1/sqrt(evd.Cxx$values)) %*% t(evd.Cxx$vectors)
  evd.Cyy = eigen(Cyy)
  Cyy.sqrt.inv = evd.Cyy$vectors %*% diag(1/sqrt(evd.Cyy$values)) %*% t(evd.Cyy$vectors)
  R = Cxx.sqrt.inv %*% Cxy %*% Cyy.sqrt.inv
  svd = svd(R)
  A = Cxx.sqrt.inv %*% svd$u[,1:ndim]
  B = Cyy.sqrt.inv %*% svd$v[,1:ndim]
  return(list(canonical.corr = svd$d[1:ndim], canonical.coef.A = A, canonical.coef.B = B))
}

############################################################################

mm <- read.csv("https://stats.idre.ucla.edu/stat/data/mmreg.csv")
colnames(mm) <- c("Control", "Concept", "Motivation", "Read", "Write", "Math", 
                  "Science", "Sex")
psych <- mm[, 1:3]
acad <- mm[, 4:8]

library(CCA)#既存のパッケージ
cc1 <- cc(psych, acad)
cc1$cor
cc1$xcoef
cc1$ycoef

CCA.my(as.matrix(psych), as.matrix(acad),3)

参考文献

Hoteling(1936).Relation between two sets of variates, Biometrika, 28, 321-277
Hardon, Szedmak, and Shawm-Taylor(2004). Canonical Correlation Analysis: An Overview with Application to Learning Methods, Neural Computation 16, 2639-2664
赤穂(2006). 正準相関分析入門 —複数種類の観測からの共通情報抽出法—, 日本神経回路学会誌, 20(2), 62-72
山下(2012). 正準相関分析の相関平方和最大化による定式化と構造行列の回転, 行動計量学, 39, 1-9

多変量解析メモ-正準相関分析(Canonical Correlation Analysis, CCA)-