1. 雑要約
今回の記事では,The elements of statistical learningから線形判別分析(Linear Discriminant Analysis, LDA)とQDA(Quadratic Discriminant Analysis)の項をまとめ,pythonでnumpy等を用いてLDAのみ実装しました.
2. LDAとQDAをおおまかに
本章では線形判別分析(Linear Discriminant Analysis, LDA)と二次判別分析(Quadratic Discriminant Analysis, QDA)をおおまかに紹介します.LDAとQDAは__ラベルありのデータから判別境界を計算することで分類を行う手法__です.グループ$G_k$の事前確率を$\pi_k$,密度関数を$f_k(x)$とすると,事後確率$Pr(G=k|X=x)$はベイズの定理を用いて,
$$Pr(G = k|X=x)=\frac{\pi_kf_k(x)}{\sum_{l=1}^K\pi_lf_l(x)}$$と表せます.表記が本当にめんどくさいので,以降$P(G=k|X=x) = P(k|x)$と書きます.まずはLDAについてのおおまかな解説を行います.
2-1. QDA
QDA,LDAは学習用のデータから,グループをうまく分類できる判別境界を求める手法です.事後確率$Pr(k|x)$が最大となるクラスに個体xが属するという基準で判別を行います.判別境界は,個体xがグループkとグループlのどちらにも属する可能性がある部分であり,それぞれの事後確率が一致するところです.これを数式で表すと,
\begin{eqnarray}
&& Pr(k|x) = Pr(l|x)\\
&\Leftrightarrow&\log Pr(k|x) = \log Pr(l|x)\\
&\Leftrightarrow&\log Pr(k|x) - \log Pr(l|x)=0\\
&\Leftrightarrow&\log\frac{Pr(k|x)}{Pr(l|x)} = 0\\
\end{eqnarray}
ここで,クラスgに属する個体がそれぞれ正規分布$N(\mu_g,\Sigma_g)$に従うとすると,その密度関数は$$f_g(x) = \frac{1}{(2\pi)^{p/2}|\Sigma_g|^{1/2}}\exp[-\frac{1}{2}(x-\mu_g)'\Sigma_g^{-1}(x-\mu_g)]$$であり,それぞれ判別境界の式は
\begin{eqnarray}
\log\frac{Pr(k|x)}{Pr(l|x)} &=& \log[\frac{\pi_kf_k(x)}{\sum_{g=1}^K\pi_gf_g(x)}\times\frac{\sum_{g=1}^K\pi_gf_g(x)}{\pi_lf_l(x)}]\\
&=& \log\frac{\pi_kf_k(x)}{\pi_lf_l(x)}\\
&=& \log\frac{\pi_k}{\pi_l} + \log\frac{f_k(x)}{f_l(x)}\\
&=& \log\frac{\pi_k}{\pi_l} - \frac{1}{2}\log\frac{|\Sigma_k|}{|\Sigma_l|}-\frac{1}{2}(x-\mu_k)'\Sigma_k^{-1}(x-\mu_k)+\frac{1}{2}(x-\mu_l)'\Sigma_l^{-1}(x-\mu_l)\\
&=&\log\frac{\pi_k}{\pi_l} - \frac{1}{2}\log\frac{|\Sigma_k|}{|\Sigma_l|}-\frac{1}{2}x'\Sigma_k^{-1}x+\mu_k'\Sigma_k^{-1}x-\frac{1}{2}\mu_k'\Sigma_k^{-1}\mu_k+\frac{1}{2}x'\Sigma_l^{-1}x-\mu_l'\Sigma_l^{-1}x+\frac{1}{2}\mu_l'\Sigma_l^{-1}\mu_l\\
&=&-\frac{1}{2}x'(\Sigma_k^{-1}-\Sigma_l^{-1})x+(\mu_k'\Sigma_k^{-1}-\mu_l'\Sigma_l^{-1})x-\frac{1}{2}\mu_k'\Sigma_k^{-1}\mu_k+\frac{1}{2}\mu_l'\Sigma_l^{-1}\mu_l+\log\frac{\pi_k}{\pi_l} - \frac{1}{2}\log\frac{|\Sigma_k|}{|\Sigma_l|}\\
&=& -\frac{1}{2}x'Ax+b_1'x+c_1=0\tag{1}\\
&&(A:=\Sigma_k^{-1}-\Sigma_l^{-1},b:=\Sigma_k^{-1}\mu_k-\Sigma_l^{-1}\mu_l,c:=-\frac{1}{2}\mu_k'\Sigma_k^{-1}\mu_k+\frac{1}{2}\mu_l'\Sigma_l^{-1}\mu_l+\log\frac{\pi_k}{\pi_l} - \frac{1}{2}\log\frac{|\Sigma_k|}{|\Sigma_l|})
\end{eqnarray}
最後の式$-\frac{1}{2}x'Ax+b_1'x+c_1=0$から,グループk,lの共分散行列が異なる(=分布の形状が異なる)ならば,判別境界は2次関数(Quadratic function)であることがわかります.事後確率が大きいクラスに分類するため,新しく得られたデータ$x_{new}$に対して,判別ルールは
\begin{eqnarray}
&&assign\ x_{new}\\
&&to\ \left\{\begin{array}{l}
Group\ k\ (if\ (1)>0)\\
Group\ l\ (otherwise)
\end{array}\right.
\end{eqnarray}
となります.実際に人工データを発生させて,sklearn.discriminant_analysis.QuadraticDiscriminantAnalysisを実行してみた結果を以下に示します.共分散行列が異なる2つの正規分布からデータが生成されたとします.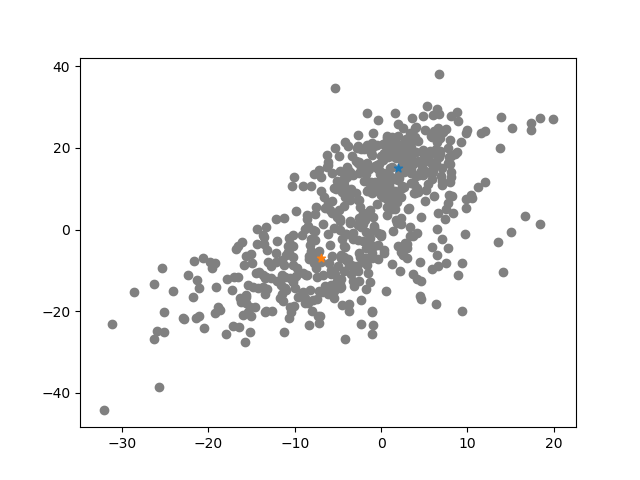
このデータに対してqdaを実行し,判別境界とともにプロットすると以下のようになります.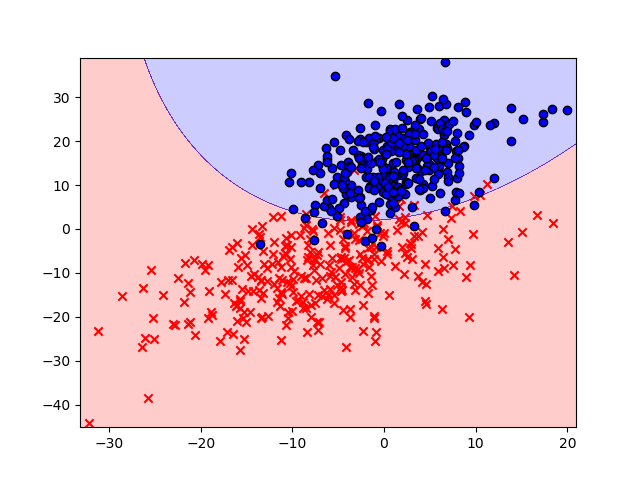
先ほどの導出で見たように,判別境界が曲線になっていることがわかります.
2-2. LDA
QDAにおいて,グループk,lの共分散行列が等しい($\Sigma = \Sigma_k=\Sigma_l$)と仮定を置いた場合,判別境界の式(1)は,
\begin{eqnarray}
\log\frac{Pr(k|x)}{Pr(l|x)} &=& -\frac{1}{2}x'(\Sigma^{-1}-\Sigma^{-1})x+(\mu_k'\Sigma^{-1}-\mu_l'\Sigma^{-1})x-\frac{1}{2}\mu_k'\Sigma^{-1}\mu_k+\frac{1}{2}\mu_l'\Sigma^{-1}\mu_l+\log\frac{\pi_k}{\pi_l} - \frac{1}{2}\log\frac{|\Sigma|}{|\Sigma|}\\
&=&(\mu_k'-\mu_l')\Sigma^{-1}x-\frac{1}{2}(\mu_k-\mu_l)'\Sigma^{-1}(\mu_k-\mu_l)+\log\frac{\pi_k}{\pi_l} - \frac{1}{2}\log1\\
&=& (\mu_k'-\mu_l')\Sigma^{-1}x-\frac{1}{2}(\mu_k-\mu_l)'\Sigma^{-1}(\mu_k-\mu_l)+\log\frac{\pi_k}{\pi_l}\\
&=& b_2'x + c_2 = 0\tag{2}\\
&&(b_2:=\Sigma^{-1}(\mu_k-\mu_l),c_2:=-\frac{1}{2}(\mu_k-\mu_l)'\Sigma^{-1}(\mu_k-\mu_l)+\log\frac{\pi_k}{\pi_l})
\end{eqnarray}
となり,判別境界が線形関数になるということがわかります.新しく得られたデータ$x_{new}$に対して,判別ルールは,
\begin{eqnarray}
&&assign\ x_{new}\\
&&to\ \left\{\begin{array}{l}
Group\ k\ (if\ (2)>0)\\
Group\ l\ (otherwise)
\end{array}\right.
\end{eqnarray}
となります.QDAと同様に,判別関数に$x_{new}$を代入した結果の正負でクラス判別を行います.QDAとLDAを実装する際に必要なのは,各クラス毎の標本平均$\widehat{\mu_g}$,標本共分散$\widehat{\Sigma_g}$,事後確率$\widehat{\pi_g}$の計算です.$n_g$をクラスgに属する要素の個数とすると,これらは,それぞれ,
\begin{eqnarray}
\hat{\mu} _g &=& \frac{1}{n_g}\sum_{x_i\in G_g}x_i\\
\hat{\Sigma}_g &=& \frac{1}{n_g-1}\sum_{x_i\in G_g}(x_i-\hat{\mu} _g)(x_i-\hat{\mu} _g)'\\
\hat{\pi_g} &=& \frac{n_g}{N}\\
\hat{\Sigma} &=& \frac{1}{N-K}\sum_{k=1}^K\sum_{x_i\in G_k}(x_i-\hat{\mu} _g)(x_i-\hat{\mu} _g)'\ \ \ (\mbox{共分散行列が等しいとき})
\end{eqnarray}
で求められます.これらを用いて,係数$A,b_1,c_1,b_2,c_1$を計算することで判別関数を求める(=モデルを学習させる)ことができます.以下では,人工データを発生させて,実際にsklearn.discriminant_analysis.LinearDiscriminantAnalysisを用いてLDAを行なっています.先ほどとは異なり,共通の共分散行列を持つ二つの正規分布からデータが発生したと考えます.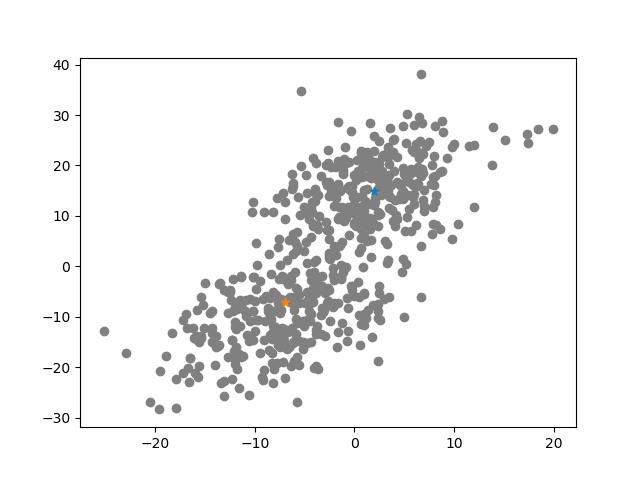
このデータに対して,ldaを行い,判別境界とともにプロットした結果が以下のようになりました.
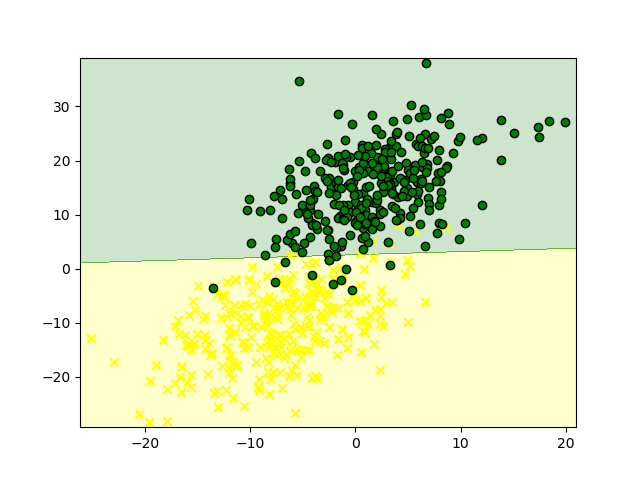
これも,導出で見たように判別境界が直線になっていることが確認できます.
(サポートベクターマシン(Support Vector Machine)も線形の境界を求める手法ですが,SVMは__サポートベクター(判別境界付近の個体.判別境界の形成に影響する)と判別境界とのマージンを最大化する__,という基準で定式化されます.)
3. Fisherの線形判別関数(4.3.3 Reduced-Rank LDAのところ)
データがクラス数Kと比較して,高次元空間に属する場合,次元を縮約することで,見通しよく分析を行うことができます.次元縮約(dimension reduction)を伴う線形判別分析について,_The elements of statistical learning_では,
The K centroids in p-dimensional input space lie in an affine subspace of dimension $\le K-1$, and if p is much larger than K, this will be considerable drop in dimension. Moreover, in locating the closest centroid, we can ignore distance orthogonal to this subspace, since they will contribute equally to each class. Thus we might just as well project the $X^*$ onto this centroid-spanning subspace $H_{K-1}$, and make distance comparison there.
と書かれています.「K($\le p$)個のクラス重心(セントロイドと言います)が,$K-1$次元の空間に存在し,変数の数pがクラス数Kと比較してかなり大きいならば,次元を大幅に削減できる.そのような場合,データを,セントロイドが張る空間$H_{K-1}$に射影して,そこで距離の比較を行えば良い.」ということですね.次元縮約を伴う線形判別分析も,主成分分析などと同様に,最適な次元を分析者が定める必要があります.Fisherはこの__最適な次元__を「射影されたセントロイドができるだけ散らばっている次元」と定めました.クラス重心のばらつきを表す群間分散行列(Between-class variance)をB,クラス内の個体のばらつきを表す群内分散行列(Within-class variance)をW,データを線形変換するための係数を格納したベクトルをaとすると,Fisherの考えた問題は,
\begin{eqnarray}
&&\underset{a}{max}\ \frac{a^TBa}{a^TWa}\\
\Leftrightarrow&&\underset{a}{max}\ a^TBa\ subject\ to\ a^TWa=1
\end{eqnarray}
というものでした.これは,__クラス内の散らばりと比較して,各クラスの重心ができるだけ散らばるようにデータXを変換するベクトルaを求める__という問題です.2行目で$$subject\ to\ a^TWa=1$$としていますが,これはベクトルaの__方向のみ__が興味の対象であり,伸縮は考慮しないということを表現しています.この問題に対するラグランジュ関数は,
\begin{eqnarray}
L(a,\theta)=a^TBa-\theta(a^TWa-1)
\end{eqnarray}
$a$について偏微分したものを0と置くと,
\begin{eqnarray}
\frac{\partial L(a,\theta)}{\partial a} &=& 2Ba-2\theta Wa = 0\\
&&\Leftrightarrow Ba =\theta Wa\\
&&\Leftrightarrow W^{-1}Ba = \theta a
\end{eqnarray}
と固有値問題の形になるので,$L(a,\theta)$を最大にするには,$\theta$を$W^{-1}B$の最大固有値,$a$をそれに対応する固有ベクトルとすれば良いということがわかります.
4. 実装例
2章で用いた図表を出力するためのコードです.LDAとQDAはsklearnのメソッドを使いました(楽しました.でも,実装するとしても,データから各群の平均と共分散行列を計算して,A,b,cに代入するだけなのでめっちゃ簡単です).判別境界のプロットでめちゃくちゃ時間とかしました.判別境界の書き方は,こちらの方のブログを参考にしました.
# coding: utf-8
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis as LDA
from sklearn.discriminant_analysis import QuadraticDiscriminantAnalysis as QDA
from sklearn.model_selection import train_test_split
# データの生成
mu1 = [2,15]; mu2 =[-7,-10]
sigma1 = [[30,20],[20,50]]; sigma2 = [[30,70],[70,40]]
np.random.seed(1)
ransu1 = np.random.multivariate_normal(mu1,sigma1,300)
np.random.seed(2)
ransu2 = np.random.multivariate_normal(mu2,sigma2,300)
np.random.seed(3)
ransu3 = np.random.multivariate_normal(mu2,sigma1,300)
# different covariance matrix
plt.scatter(ransu1[:,0],ransu1[:,1],c="gray")
plt.scatter(mu1[0],mu1[1],marker="*")
plt.scatter(ransu2[:,0],ransu2[:,1],c="gray")
plt.scatter(mu2[0],mu2[0],marker="*")
plt.savefig("適当なディレクトリ")
plt.show()
# the same covariance matrix
plt.scatter(ransu1[:,0],ransu1[:,1],c="gray")
plt.scatter(mu1[0],mu1[1],marker="*")
plt.scatter(ransu3[:,0],ransu3[:,1],c="gray")
plt.scatter(mu2[0],mu2[0],marker="*")
plt.savefig("適当なディレクトリ")
plt.show()
def plot_boundary(y,x,model,c,mark,path,interval=0.01):
"""
y: class label
x: variables of data
model: the model estimated from training data
c: color map
mark: marker
path: file path
interval: interval of mesh
"""
v1_min, v1_max = x[:,0].min()-1, x[:,0].max()+1
v2_min, v2_max = x[:,1].min()-1, x[:,1].max()+1
v1_mesh, v2_mesh = np.meshgrid(np.arange(v1_min,v1_max,interval),np.arange(v2_min,v2_max,interval))
z = model.predict(np.array([v1_mesh.ravel(),v2_mesh.ravel()]).T)
z = z.reshape(v1_mesh.shape)
#等高線のプロット ,alpha:色の透明度の調整
plt.contourf(v1_mesh,v2_mesh,z,alpha=0.2,cmap=cmap)
plt.xlim(v1_mesh.min(), v1_mesh.max())
plt.ylim(v2_mesh.min(), v2_mesh.max())
for idx, cl in enumerate(np.unique(y)):
plt.scatter(x=x[y == cl, 0],y=x[y == cl, 1],alpha = 1,c=cmap(idx),edgecolors="black",marker=mark[idx],label=cl)
plt.savefig(path)
plt.show()
return None
# 共分散同じ
data1 = np.hstack([np.vstack([ransu1,ransu3]),np.vstack([np.ones(300),np.zeros(300)]).reshape(600,1)])
X_same_train, X_same_test, y_same_train, y_same_test = train_test_split(data1[:,:2],data1[:,2],test_size=0.2,random_state=88)
# 共分散違う
data2 = np.hstack([np.vstack([ransu1,ransu2]),np.vstack([np.ones(300),np.zeros(300)]).reshape(600,1)])
X_diff_train, X_diff_test, y_diff_train, y_diff_test = train_test_split(data2[:,:2],data2[:,2],test_size=0.2,random_state=44)
markers = ('x', 'o')
# パッケージの利用(LDA)
cmap = ListedColormap(("yellow","green"))
lda = LDA()
lda.fit(X_same_train,y_same_train)#モデル作成
predict_lda = lda.predict(X_same_test)
print("miss-classification rate(LDA)",np.round(np.sum(np.abs(predict_lda-y_same_test))/y_same_test.shape[0],3))
plot_boundary(data1[:,2],data1[:,[0,1]],lda,cmap,markers,"適当なパス")
# パッケージの利用(QDA)
qda = QDA()
qda.fit(X_diff_train,y_diff_train)#モデル作成
predict_qda = qda.predict(X_diff_test)
print("miss-classification rate(QDA)",np.round(np.sum(np.abs(predict_qda-y_diff_test))/y_diff_test.shape[0],3))
# cmap_summer = plt.get_cmap("summer")
cmap = ListedColormap(("red","blue"))
plot_boundary(data2[:,2],data2[:,[0,1]],qda,cmap,markers,"適当なパス")
ldaとqdaの分類モデルは,データを8:2の割合で訓練データとテストデータに分割して,訓練データで学習させました.テストデータでの誤判別率は,それぞれ,ldaが0.05,qdaが0.033となりました.まあまあの精度です.是非パラメータ弄って実行してみてください.
参考文献
Hastie, Trevor, Tibshirani, Robert, Friedman, Jerome(2009).The elements of statistical learning