「天気図っぽい前線」は気象データのどこを見て描かれているのか?(2) Grad-CAM++のセマンティックセグメンテーションへの適用と実装
0.はじめに
実施したこと
・Grad-CAM++をセマンティックセグメンテーションに適用し、実装した。
・気象図から前線を検出するニューラルネットワークに適用して可視化結果を見てみた。
今回の内容
前回の投稿では、Seg-Grad-CAMを用いて「天気図っぽい前線」のニューラルネットワークの注視領域の可視化を行いました。
前回の投稿:
天気図っぽい前線」はデータのどこを見て描かれているのか?(1) Grad-CAMのセマンティックセグメンテーションへの適用
Grad-CAMには発展型のGrad-CAM++があります。
Grad-CAM++をセマンティックセグメンテーションに適用した事例というのが見当たらなかったので、原論文や参考文献をもとに、今回実装をしてみました。思想というか方式としては、Grad-CAMがSeg-Grad-CAMに適用された上述の論文のものと同じです。
目次
1.Grad-CAM++概説
2.セマンティックセグメンテーションへの拡張
3.Kerasによる実装
4.可視化例
5.終わりに
6.参考文献
1.Grad-CAM++概説
(1)Grad-CAM++とは
Aditya Chattopadhyay, Anirban Sarkar and Vineeth N Balasubramanianによる論文Grad-CAM++: Improved Visual Explanations for Deep Convolutional Networksで提唱された方法です。
CNNが画像を分類するにあたって画像の部位ごと影響の大小を可視化する手法のひとつです。
論文の内容については、こちらの記事でたいへん丁寧にわかりやすく紹介されています。
最新手法!「Grad-CAM++」のレビューと実装
(2)Grad-CAM++の数式
CNNの線形結合による表現
画像分類のCNNが、画像を入力として与えるときに、それがいくつかのクラスのうち、クラスCと分類された最終スコアを$Y^c$とします。
あるconvolution層の出力(Activation mapと呼ばれる)を$A^k_{ij}$とします。i,j,kはActivation mapのピクセル位置(横、縦)、チャンネルを表すインデックスです。
このとき$Y^c$を、
\begin{align}
Y^c &= \sum_k w^c_k \sum_i\sum_j A^k_{ij} \tag 1 \\
&= \sum_i \sum_j( \sum_k w^c_k A^k_{ij}) \tag 2 \\
\end{align}
と表されるとします。式(1)は最終スコアを、あるActivation mapの線形結合で表現している形です。
一般にCNNではsigmoidであったり非線形項を含んだりするので、厳密に成り立つわけではないと思います。
ですから、Grad-CAMの原論文(Grad-CAM: Visual Explanations from Deep Networks via Gradient-based Localization)でも記載されているように、$A^k$以降のCNNについて線形化近似しているような感じです。
この数式は、式(2)の形式にしてみるとConvolution層のピクセルと最終スコアの関係にもなっています。
ヒートマップ
Grad-CAMやGrad-CAM++は以下の形式で$L^c$を定義してヒートマップとしています。
L^c_{ij} = \sum_{k}w_k^cA_{ij}^k \tag 3
Grad-CAMでは、式(1)の両辺を$A^k_{ij}$で偏微分してwを得ています。式導出は原論文をご参照ください。
結果は次のようになります。
w_k^c = \dfrac{1}{Z}\sum_i\sum_j\dfrac{\partial Y^c}{\partial A_{ij}^k} \tag 4
$Z$はActivation Mapのピクセル数ですので、勾配を各チャネルの画像に渡って平均した数値を重みとして、Activation mapを足し合わせたものをヒートマップとしていることになります。
Grad-CAM++
これに対してGrad-CAM++では、Activation Mapの重み付き線形結合を取ることは同じですが、その際の重みは勾配を単純平均するのではなく、ピクセルに異なる値の重み$\alpha_{ij}^{kc}$をつけて足しています。
\begin{align}
Y^c &= \sum_k w^c_k \sum_l\sum_m A^k_{lm} \tag 5 \\
w_k^c &= \sum_i\sum_j\alpha_{ij}^{kc}relu\left(\dfrac{\partial Y^c}{\partial A_{ij}^k}\right) \tag 6
\end{align}
この$\alpha_{ij}^{kc}$の導出は原論文やQiitaの解説記事にありますが、式(6)を式(5)に代入して得られる式
Y^c = \sum_k (\sum_i\sum_j\alpha_{ij}^{kc}relu\left(\dfrac{\partial Y^c}{\partial A_{ij}^k}\right)) \sum_l\sum_m A^k_{lm} \tag 7
の両辺を$A^k_{ij}$で偏微分していくことで得られます。
\alpha_{ij}^{kc} = \dfrac{\dfrac{\partial^2Y^c}{(\partial A_{ij}^k)^2}}{2\dfrac{\partial^2Y^c}{(\partial A_{ij}^k)^2}+\sum_l\sum_m A_{lm}^k\left\{\dfrac{\partial^3Y^c}{(\partial A_{ij}^k)^3}\right\}} \tag 8
ここで2階偏微分や3階偏微分が出てきますが、これらを巧妙な方法で、最終クラスの算出層の一つ手前の層の出力の1階微分を用いて表現することで、Keras/TensorflowやPytorchといったフレームワークの勾配算出機能を用いることが可能なようにしているのが原論文です。
最終層がsoftmaxの場合
これも原論文で説明されていますが、最終層がsoftmaxの場合は、softmax層に入る一つ前の層の出力を$S^c_{ij}$とすると、
Y^c_{ij} = \dfrac{\exp(S^c_{ij})}{\sum_k \exp(S^k_{ij})} \tag{9}
となります。
後ほど、式(8)(9)から計算可能な表現を導き出していきますが、後ほどセマンティックセグメンテーションへの拡張の中で、導出を追いかけることとします。
2.セマンティックセグメンテーションへの拡張
(1)拡張の方法
拡張の方法は、Grad-CAMをSeg-Grad-CAMへ拡張した方式同じです。
最終出力で、クラスCに分類された関心のある領域について、ピクセルごとのヒートマップを計算し足し合わせます。
下図で、右側の出力図の赤、青、ピンクに分類されたピクセル1点ごとに、Grad-CAM++の手法によってヒートマップを作成します。このピクセルの数分だけ作成されたヒートマップを最後に足し合わせたものを求めるヒートマップとするというものです。
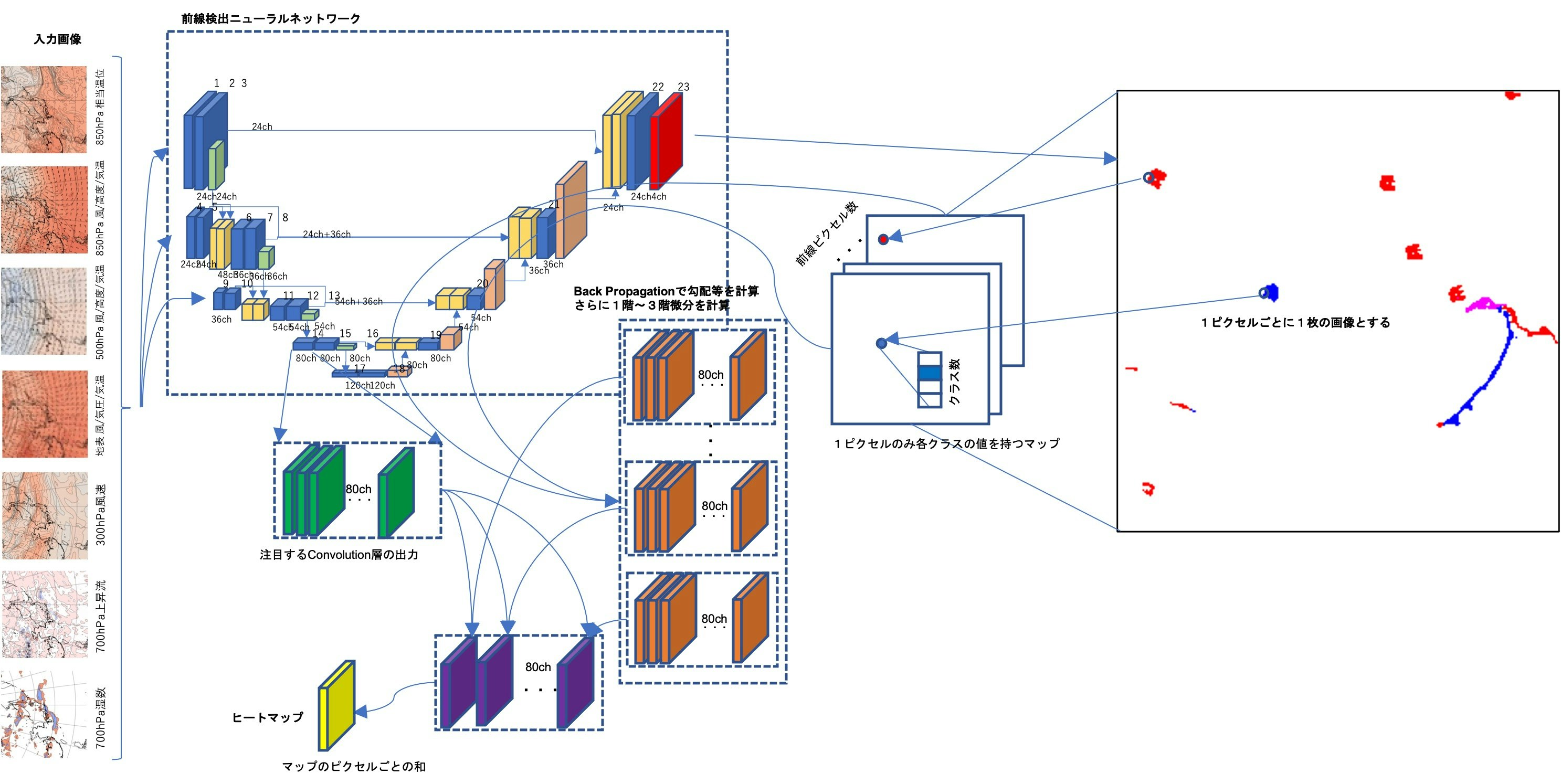
図 Grad-CAM++のセマンティックセグメンテーションへの拡張 概念図
(2)数式の導出
解くべき数式
ヒートマップを計算する際に、Keras バックエンド関数を用いて計算できるような量で表すことを目的に、数式を展開します。
最終スコアがクラスcと分類された領域に対して、その領域に所属するピクセル(u,v)のスコアYを$Y^c_{uv}$と表します。
softmaxに渡される数値を同様に$S^c_{uv}$とすると、YとSの間には、次の関係があります。
Y^c_{uv} = \dfrac{\exp(S^c_{uv})}{ \sum_k \exp(S^k_{uv})} \tag{10}
Activation mapの勾配は先程の実装方針のとおり、ピクセル毎のヒートマップの和になりますので、
\dfrac{\partial Y^c}{\partial A^l_{ij}} = \sum_{uv \in \mathcal{M} } \dfrac{\partial Y^c_{uv}}{\partial A^l_{ij}} = \sum_{uv \in \mathcal{M} } \dfrac{\partial}{\partial A^l_{ij}} \dfrac{\exp(S^c_{uv})}{\sum_k \exp(S^c_{uv})} \tag {11} \\
となります。
なお式(11)では最終スコアのクラスを示すkとActivation mapのチャネルを示すlを別の添字として分けました。
原論文ではどちらも同じkで表現されていますが、混乱を避けるため本稿では別にしました。
各変数の導出
原論文でも数式が示されていますが、実装するためには一度式導出をやっておくと理解が深まります。
ニューラルネットワークのForward Propagationを実行して得られるのは、
$Y^c_{uv}$ :最終層(softmax)の出力
$S^c_{uv}$ :最終層(softmax)の一つ前層の出力
$\dfrac{\partial S^c_{uv}}{\partial A^l_{ij}}$ : backend関数を用いて計算
の3つです。
式(11)を展開して、これら3つの値で表せるようにする必要があります。
1階微分の算出
少し式展開を明示しながら展開してみます。
式(11)は、偏微分の連鎖律によって
\begin{align}
&f=\exp(S^k_{uv}) \\
&g=\sum_k \exp(S^k_{uv})\\
&\dfrac{\partial f}{\partial A^l_{ij}}=\exp(S^k_{uv})\dfrac{\partial S^k_{uv}}{\partial A^l_{ij}} \\
&\dfrac{\partial g}{\partial A^l_{ij}}=\sum_k (\exp(S^k_{uv})\dfrac{\partial S^k_{uv}}{\partial A^l_{ij}} )
\end{align}
であること、分数関数の微分が
\dfrac{d}{dx} \dfrac{f(x)}{g(x)} = \dfrac{f'g - fg'}{g^2}
であることに注意すれば、
\begin{align}
\dfrac{\partial Y^c_{uv}}{\partial A^l_{ij}} &=
\dfrac{
\exp(S^c_{uv})\dfrac{\partial S^c_{uv}}{\partial A^l_{ij}} \sum_k \exp(S^k_{uv})
- \exp(S^c_{uv})\sum_k (\exp(S^k_{uv})\dfrac{\partial S^k_{uv}}{\partial A^l_{ij}})
}
{ ( \sum_k \exp(S^k_{uv}) ) ^2 } \\
&=
\dfrac{\exp(S^c_{uv})}{\sum_k \exp(S^k_{uv})}
\left[
\dfrac{\partial S^c_{uv}}{\partial A^l_{ij}}
- \dfrac{
\sum_k (\exp(S^k_{uv})\dfrac{\partial S^k_{uv}}{\partial A^l_{ij}})
}{
\sum_k \exp(S^k_{uv})
}
\right] \\
&= Y^c_{uv}
\left[
\dfrac{\partial S^c_{uv}}{\partial A^l_{ij}}
- \sum_k (\dfrac{ \exp(S^k_{uv})}{ \sum_{k'} \exp(S^{k'}_{uv}) } \dfrac{\partial S^k_{uv}}{\partial A^l_{ij}})
\right] \tag{11A} \\
&= Y^c_{uv}
\left[
\dfrac{\partial S^c_{uv}}{\partial A^l_{ij}}
- \sum_k (Y^k_{uv} \dfrac{\partial S^k_{uv}}{\partial A^l_{ij}})
\right] \tag {12}
\end{align}
となります。
式(11A)では、その前の段階で、括弧内の分母にクラスについて和を取る式$\sum_k \exp(S^k_{uv})$が出てきます。和を取ったものはkに依らなくなりますので、分子の総和記号の中に入れてしまうことができます。
その上で、下記の関係を利用して式(12)の形に変形しています。
Y^k_{uv} = \dfrac{ \exp(S^k_{uv})}{ \sum_{k'} \exp(S^{k'}_{uv}) }
2階微分、3階微分の計算
同様にして式(12)を微分して、Yの2階微分、3階微分を計算していきます。
このとき、$S^c$のActivation mapに関する2階微分は、Relu関数の2階微分を含むためにゼロになる、という性質を利用しています。
まず2階微分を導出します。
\begin{align}
\dfrac{\partial^2 Y^c_{uv}}{(\partial A^l_{ij})^2}
& = \dfrac{\partial Y^c_{uv}}{\partial A^l_{ij}}
\left[
\dfrac{\partial S^c_{uv}}{\partial A^l_{ij}}
- \sum_k (Y^k_{uv} \dfrac{\partial S^k_{uv}}{\partial A^l_{ij}})
\right] \\
&+ Y^c_{uv}
\left[
T(S'')
- \sum_k \left[
(\dfrac{\partial Y^k_{uv}}{\partial A^l_{ij}}
\dfrac{\partial S^k_{uv}}{\partial A^l_{ij}})
- Y^k_{uv} \times T(S'')
\right]
\right]\\
&= \dfrac{\partial Y^c_{uv}}{\partial A^l_{ij}}
\left[
\dfrac{\partial S^c_{uv}}{\partial A^l_{ij}}
- \sum_k (Y^k_{uv} \dfrac{\partial S^k_{uv}}{\partial A^l_{ij}})
\right] - Y^c_{uv}
\sum_k
(\dfrac{\partial Y^k_{uv}}{\partial A^l_{ij}}
\dfrac{\partial S^k_{uv}}{\partial A^l_{ij}})
\tag{14}
\end{align}
ここで$T(S'')$はSのAに関する2階微分の項を示しており、ゼロになります。
次に3階微分です。$T(S'')$をゼロとしながら式(14)の偏微分を行うと、
\begin{align}
\dfrac{\partial^3 Y^c_{uv}}{(\partial A^l_{ij})^3}
&= \dfrac{\partial^2 Y^c_{uv}}{(\partial A^l_{ij})^2}
\left[
\dfrac{\partial S^c_{uv}}{\partial A^l_{ij}}
- \sum_k (Y^k_{uv} \dfrac{\partial S^k_{uv}}{\partial A^l_{ij}})
\right] \\
&+ \dfrac{\partial Y^c_{uv} }{\partial A^l_{ij}}
\left[ T(S'') - \sum_k
(\dfrac{\partial Y^k_{uv}}{\partial A^l_{ij}}
\dfrac{\partial S^k_{uv}}{\partial A^l_{ij}} )
-\sum_k(Y^k_{uv} \times T(S'') )
\right] \\
&- \dfrac{\partial Y^k_{uv}}{\partial A^l_{ij}}\sum_k
(\dfrac{\partial Y^k_{uv}}{\partial A^l_{ij}}
\dfrac{\partial S^k_{uv}}{\partial A^l_{ij}} )
- Y^c_{uv}
\sum_k \left[
\dfrac{\partial^2 Y^k_{uv}}{(\partial A^l_{ij})^2}
\dfrac{\partial S^k_{uv}}{\partial A^l_{ij}}
+ \dfrac{\partial^2 Y^k_{uv}}{(\partial A^l_{ij})^2} \times T(S'')
\right] \\
&= \dfrac{\partial^2 Y^c_{uv}}{(\partial A^l_{ij})^2}
\left[
\dfrac{\partial S^c_{uv}}{\partial A^l_{ij}}
- \sum_k (Y^k_{uv} \dfrac{\partial S^k_{uv}}{\partial A^l_{ij}})
\right]
- 2\dfrac{\partial Y^c_{uv} }{\partial A^l_{ij}}
\sum_k
(\dfrac{\partial Y^k_{uv}}{\partial A^l_{ij}}
\dfrac{\partial S^k_{uv}}{\partial A^l_{ij}}) \\
&- Y^c_{uv}
\sum_k
(\dfrac{\partial^2 Y^k_{uv}}{(\partial A^l_{ij})^2}
\dfrac{\partial S^k_{uv}}{\partial A^l_{ij}}) \tag{15}
\end{align}
が得られます。
なお原論文では$A^k_{ij}$のように、Activation mapのチャネル成分がkで表記されています。
しかしながら、最終スコアのクラス成分もkで表現されているので、実装時の混乱を避けるため、この投稿では$A^l_{ij}$という記載とするようにします。
式(13)〜(15)を式(8)に代入して、(u,v)で和を取れば重み$\alpha^{kc}_{ij}$が求まります。
3.Kerasによる実装
2.で検討した数式に沿って、実装します。
なお私の環境は以下のとおりです。
Mac miniのCPU環境です。GPGPUは使用していません。
ハードウェア:Mac mini(2018)
プロセッサ:3.2GHz 6core Intel Core i7
メモリ:32GB 2667MHz DDR4
OS:macOS Big Sur
anaconda:anaconda3-5.3.1
Python:Python 3.7.2
tensorflow:1.13.1 conda-forge
Keras:2.2.4
keras-preprocessing:1.1.0
今回の参考実装がTensorflow 1系であったため少し古いソフトウェア環境となっています。
(1)学習済CNNのテンソルの使い方
$\partial S^c_{uv}/\partial A^l_{ij}$という量は、インデックスが6個のテンソルとなっています。
出力層の一つ前の層の成分(クラス数と画像サイズ)、とヒートマップを作りたい別のConvolution層の出力の成分(チャネル数と画像サイズ)を同時に持っているためです。
学習済みのCNNは一般的な
(バッチ数✕チャネル数✕画像サイズ横✕画像サイズ縦)
という成分のテンソルを使っていますので、直接にこれを導入するわけに行きません。
バックエンド関数(KTF.gradient)を利用するところでは、学習済CNNと同じdimensionとする必要があります。
そこで(u,v)について、クラスCと分類されるピクセルのリストとして1次元化します。
そして、CNNのテンソルで使わない、バッチ数の次元のところにこのピクセルリスト成分をあてはめます。
これによって、勾配計算に使用するテンソルは、
(クラスCと分類されるピクセルリスト数✕クラス数✕出力画像サイズ横✕出力画像サイズ縦)
という4階テンソルになります。
バックエンド関数を用いて、Convolution層で得られる勾配は、
(クラスCと分類されるピクセルリスト数✕Activation mapのチャネル数✕Activation map画像サイズ横✕Activation map画像サイズ縦)
という次元です。
(2) 実装する
Forward Propagationの実行と対象ピクセル領域の決定
まず、学習済ネットワークを呼び出して、Forward Propagationを実行し、前線としてクラス分類されたピクセル群を特定します。
import keras.backend.tensorflow_backend as KTF # Keras backend 関数のimport
(中略)
"""
学習済ネットワークと重みを呼び出す
"""
NN_1 = load_model(paramfile, \
custom_objects={'softMaxAxis': softMaxAxis })
NN_1.load_weights(weightfile)
NN_1.compile(optimizer='adam', loss='categorical_crossentropy' , \
metrics=['accuracy'])
(中略)
"""
Forward Propagationの実行
"""
# 入力データ(3入力1出力)を用意
prepro_input = [ \
np.expand_dims(np_i_data_tr[c_datalist], 0),\
np.expand_dims(np_i_128data_tr[c_datalist],0),\
np.expand_dims(np_i_64data_tr[c_datalist] ,0) ]
# 予測処理実行(Forward Propagation)
np_p_data = NN_1.predict(prepro_input)
np_p_data = np.transpose(np_p_data,(0,2,3,1)) # channels lastに転置
w_array = np_p_data[0]
prop_from_layer = "activation_1" # 最終層の名称
prop_scnd_layer = "conv2d_23" # 最終層のひとつ前の層
# ヒートマップを出力する対象層のリスト
output_layers_list = [ 'conv2d_2' , 'conv2d_3' , 'conv2d_7' ,\
'conv2d_8' , 'conv2d_12' , 'conv2d_13',\
'conv2d_15', 'conv2d_16' , 'conv2d_17',\
'conv2d_18', 'conv2d_19' , 'conv2d_20',\
'conv2d_21', 'conv2d_22']
# 最終画像の予測クラスの配列を作成
max_preds = w_array.argmax(axis=-1)
# 対象層についてのループ
for prop_to_layer in output_layers_list :
y_c_o = NN_1.get_layer(prop_from_layer).output #最終層の出力を取得
s_c_o = NN_1.get_layer(prop_scnd_layer).output #最後から2番めの層の出力を取得
conv_output = \
NN_1.get_layer(prop_to_layer ).output #ヒートマップを見たい層の出力を取得
for cnt in range(1, 4): # デフォルトクラスの0以外のクラスについて繰り返し
# クラスに属するピクセル領域(Region of Interest, RoI)を示す配列を初期化
roi = np.zeros((1,w_array.shape[0],w_array.shape[1]))
if _flag == True:
# 注目領域を左下(_llc_x, _llc_y)、右上(_ruc_x, _ruc_y)の
# 矩形領域(RoIb)に絞る場合
roib = np.zeros((w_array.shape[0],w_array.shape[1]))
roib[ _ruc_y:_llc_y+1, _llc_x:_ruc_x+1 ] = 1.0
else:
# 矩形領域に絞らない場合
roib = np.ones((w_array.shape[0],w_array.shape[1])) # all 1の配列
# Forward Prop. の結果からRoIに含まれる領域を抽出
roi = np.round( \
w_array[:,:,cls] * ( max_preds == cls ) \
).reshape(w_array.shape[0], w_array.shape[1])
#RoIに含まれており、かつRoIbに含まれている
#ピクセル座標(Point of Interest, PoI)を取得
poi_lst = np.where( ( max_preds == cls ) & ( roib > 0.0 ) )
#PoI座標のリスト x クラス数 x 画像サイズ横 x 画像サイズ縦 の配列を初期化
poi = np.zeros((len(poi_lst[0]), w_array.shape[2] , \
w_array.shape[0], w_array.shape[1] ) )
# PoI座標に1をセットする(1要素のみ1の配列がPoIピクセルの数だけ出来る)
# マスク配列となる
for cnt_poi in range(len(poi_lst[0])):
aa, bb = poi_lst[0][cnt_poi], poi_lst[1][cnt_poi]
poi[cnt_poi:cnt_poi+1, : , aa:aa+1, bb:bb+1 ] = 1
# 出力クラスY及び一つ前の出力S配列をPoI座標分繰り返す
y_c_o_poi = KTF.repeat_elements(y_c_o , len(poi_lst[0]), 0)
s_c_o_poi = KTF.repeat_elements(s_c_o , len(poi_lst[0]), 0)
# マスク配列と掛け合わせることで、出力クラスの配列、一つ前の出力のPoIに
# 合致する部分のみが有効となった配列が出来上がる
y_c = y_c_o_poi[:,:,:,:] * \
poi.reshape((len(poi_lst[0]),w_array.shape[2], \
w_array.shape[0], w_array.shape[1]))
s_c = s_c_o_poi[:,:,:,:] * \
poi.reshape((len(poi_lst[0]),w_array.shape[2], \
w_array.shape[0], w_array.shape[1]))
ここまでで、Forward Propagationを実行して、対象として取り出したいピクセル分を特定することができました。
取り出したいピクセルのみ有効な値がセットされている出力層のテンソルy_cと、ひとつ前の層のテンソルs_cを作ることができました。
Sの勾配計算を行う
次に、s_cの勾配計算を行います。
計算の途中では、出力層のチャネルと注目するConvolution層のActivation mapのチャネルの両方を持つ変数が必要になるので、最初に定義します。
co_shp0, co_shp1, co_shp2 = \
conv_output[0].shape[0], conv_output[0].shape[1], \
conv_output[0].shape[2]
G_grads1_y = KTF.zeros((1, 1, co_shp0, co_shp1, co_shp2)
G_grads2_y = KTF.zeros((1, 1, co_shp0, co_shp1, co_shp2)
G_grads3_y = KTF.zeros((1, 1, co_shp0, co_shp1, co_shp2)
G_grads1_S = KTF.zeros((1, 1, co_shp0, co_shp1, co_shp2)
# Sの勾配をバックエンド関数で定義する
# クラスCに所属するピクセルのC以外も含む成分も必要
for cnt_k in range(4):
grads1_s = KTF.gradients( s_c[:, cnt_k:cnt_k+1, :, :], conv_output )[0]
if cnt_k == 0 :
G_grads1_s = KTF.expand_dims( grads1_s , 1 )
else:
G_grads1_s = KTF.concatenate(\
[G_grads1_s, KTF.expand_dims(grads1_s, 1 )] \
,axis=1 )
G_grads1_sが、$\partial S^c_{uv}/\partial A^l_{ij}$ に相当します。
$\partial S^c_{uv}/\partial A^l_{ij}$ :(PoI配列数、出力クラス番号、Activation mapチャネル数、Activation map画像サイズ横、Activation map画像サイズ縦)
Yの勾配計算に必要な準備
この先の計算で、このG_grads1_sと出力層の出力で、G_grads1_sとはdimensionの異なる次のテンソルy_cすなわち
$Y^c_{uv}$ :最終層のdimension(PoI配列数、出力クラス数、出力画像サイズ横、出力画像サイズ縦)
との掛け算を計算する必要があります。Tensorではbroad cast計算が出来ないため、dimensionを揃える必要があります。
テンソル(y_c)は、あるPoI配列番号に対しては有効なのは1ピクセルのみでした。この1ピクセルの値を、PoI配列番号の同じG_grads_1のActivation mapの画像サイズ、チャネル数分のピクセル(第2〜5成分)にかければよいです。
そのことを踏まえて、$Y^c_{uv}, S^c_{uv}$を次のようにしてdimensionを変更します。
1.出力画像サイズ(縦×横)でバックエンド関数(KTF.sum)を利用し和を取り次元(第2,3成分)を縮約)。
和をとるといっても、1ピクセルしか値が入っていないので、1ピクセル分の値に等しくなります。
2.縮約したテンソルに、バックエンド関数(KTF.expand_dims)を使ってActivation mapのチャネル数、画像サイズ(横、縦)の成分を追加。
3.追加したActivation map成分のサイズになるように、バックエンド関数(KTF.repeat_elements)を用いて値を繰り返す。各成分に、もとの1ピクセルの値が入ったものができます。
y_c_k = KTF.sum( y_c , axis=[2,3] )
y_c_k = KTF.repeat_elements(KTF.expand_dims(y_c_k , -1), co_shp0 , -1 )
y_c_k = KTF.repeat_elements(KTF.expand_dims(y_c_k , -1), co_shp1 , -1 )
y_c_k = KTF.repeat_elements(KTF.expand_dims(y_c_k , -1), co_shp2 , -1 )
y_c_c = y_c_k[:, cls:cls+1 , : , : , : ]
y_c_cはy_c_kのうちで、着目しているクラスのみを取り出した配列です。
Yの偏微分の実装
それではYの1階微分を計算します。数式は式(12)です。
再掲しておきます。
\dfrac{\partial Y^c_{uv}}{\partial A^l_{ij}}= Y^c_{uv}
\left[
\dfrac{\partial S^c_{uv}}{\partial A^l_{ij}}
- \sum_k Y^k_{uv} \dfrac{\partial S^k_{uv}}{\partial A^l_{ij}}
\right] \tag {12}
# Yの1階偏微分を計算する
for cnt_k in range(4):
grads1_y = \
y_c_c[:,0:1, :, :, :] * \
( \
G_grads1_s[:, cls:cls+1, :, :, :] \
- KTF.sum( y_c_k * G_grads1_s, axis=1, keepdims=True )\
)
if cnt_k == 0 :
G_grads1_y = grads1_y
else:
G_grads1_y = KTF.concatenate([G_grads1_y , grads1_y ], axis=1 )
出力クラスの成分について、バックエンド関数(KTF.concatenate)を使って追加していっています。
これもNumpyの感覚であれば成分を指定して代入できそうに思えるのですが、テンソルの場合は成分指定代入を行おうとするとエラーになるための苦しい実装です。
2階、3階微分
同様にYの2階微分や、Yの3階微分を計算します。
式は(14),(15)です。これも再掲しておきます。
\begin{align}
\dfrac{\partial^2 Y^c_{uv}}{(\partial A^l_{ij})^2} &=
\dfrac{\partial Y^c_{uv}}{\partial A^l_{ij}}
\left[
\dfrac{\partial S^c_{uv}}{\partial A^l_{ij}}
- \sum_k Y^k_{uv} \dfrac{\partial S^k_{uv}}{\partial A^l_{ij}}
\right] - Y^c_{uv}
\sum_k
\dfrac{\partial Y^k_{uv}}{\partial A^l_{ij}}
\dfrac{\partial S^k_{uv}}{\partial A^l_{ij}} \\
\dfrac{\partial^3 Y^c_{uv}}{(\partial A^l_{ij})^3} &=
\dfrac{\partial^2 Y^c_{uv}}{(\partial A^l_{ij})^2}
\left[
\dfrac{\partial S^c_{uv}}{\partial A^l_{ij}}
- \sum_k Y^k_{uv} \dfrac{\partial S^k_{uv}}{\partial A^l_{ij}}
\right]
- 2\dfrac{\partial Y^c_{uv} }{\partial A^l_{ij}}
\sum_k
\dfrac{\partial Y^k_{uv}}{\partial A^l_{ij}}
\dfrac{\partial S^k_{uv}}{\partial A^l_{ij}} \\
&- Y^c_{uv}
\sum_k
\dfrac{\partial^2 Y^k_{uv}}{(\partial A^l_{ij})^2}
\dfrac{\partial S^k_{uv}}{\partial A^l_{ij}}
\end{align}
# Yの2階偏微分の計算
for cnt_k in range(4):
grads2_y = \
G_grads1_y[:,cls:cls+1,:,:,:]\
*(\
G_grads1_s[:,cls:cls+1,:,:,:] \
- KTF.sum( y_c_k * G_grads1_s, axis=1 , keepdims=True)\
) \
- y_c_c[:,0:1,:,:,:] \
* KTF.sum( G_grads1_y * G_grads1_s , axis=1, keepdims=True )
if cnt_k == 0 :
G_grads2_y = grads2_y
else:
G_grads2_y = KTF.concatenate( [ G_grads2_y , grads2_y ] , axis=1 )
#3階編微分
for cnt_k in range(4):
grads3_y = \
G_grads2_y[:,cls:cls+1,:,:,:] \
* ( \
G_grads1_s[:,cls:cls+1,:,:,:] \
- KTF.sum( y_c_k * G_grads1_s, axis=1, keepdims=True )\
) \
- 2 * grads1_y \
* KTF.sum( G_grads1_y * G_grads1_s , axis=1 , keepdims=True) \
- y_c_c[:,0:1,:,:,:] \
* KTF.sum( G_grads2_y * G_grads1_s , axis=1 , keepdims=True)
if cnt_k == 0:
G_grads3_y = grads3_y
else:
G_grads3_y = KTF.concatenate( [ G_grads3_y , grads3_y ] , axis=1 )
これでバックエンド関数を用いたヒートマップの各項目($Y^c$の1階微分、2階微分、3階微分)の計算ができました。
αおよびwの計算
これ以降は従来のGrad-CAM++と同じ計算になってきますので、adityac94/Grad_CAM_plus_plusを参考にしております。
違いは、PoI配列分をバッチ数の次元で使用しているので、テンソル計算の関数の中で$\alpha^{ck}_{ij}, w^c_k$を計算してしまうところです。
偏微分各項目を式(8),(6),(5)に代入していくことで、目指すヒートマップ$L^c_{ij}$を計算していきます。
\begin{align}
\alpha_{ij}^{kc} &= \dfrac{\dfrac{\partial^2Y^c}{(\partial A_{ij}^k)^2}}{2\dfrac{\partial^2Y^c}{(\partial A_{ij}^k)^2}+\sum_l\sum_m A_{lm}^k\left\{\dfrac{\partial^3Y^c}{(\partial A_{ij}^k)^3}\right\}} \tag 8 \\
w_k^c &= \sum_i\sum_j\alpha_{ij}^{kc}relu\left(\dfrac{\partial Y^c}{\partial A_{ij}^k}\right) \tag 6 \\
L^c_{ij} &= \sum_{k}w_k^cA_{ij}^k \tag 3
\end{align}
# Activation map(A)の画像全体での和を計算
G_sum = KTF.sum(conv_output, axis=[2,3] , keepdims=True)
# αの分子を計算
Alpha_num = G_grads2_y[:,cls:cls+1,:,:,:]
# αの分母を計算 ゼロ割を避けるため微小量を付加
Alpha_denom = G_grads2_y[:,cls:cls+1,:,:,:] * 2.0 \
+ G_grads3_y[:,cls:cls+1,:,:,:] * G_sum + KTF.epsilon()
# αを計算
Alpha_s = Alpha_num / Alpha_denom
# αを画像サイズの和で正規化
Alpha_s_max = KTF.sum( Alpha_s , axis=[3,4] , keepdims=True)
Alpha_s = Alpha_s / Alpha_s_max
# Yの勾配についてRelu適用
Weights = KTF.relu( G_grads1_y[:,cls:cls+1,:,:,:] )
# 重みwの計算
WW_AA = KTF.reshape(KTF.sum( Alpha_s * Weights, axis=[3,4] , keepdims=True), \
(len(poi_lst[0]),conv_output[0].shape[0],1,1) )
# Activationマップの重みwで結合する
D_wights = KTF.sum( WW_AA * conv_output, axis=1)
# PoIのピクセル全体での和を取る
CMAP = KTF.sum( D_wights, axis=0)
# ここまでの計算を関数として定義
gradient_function = KTF.function([NN_1.input[0], NN_1.input[1], NN_1.input[2]], [CMAP] )
# 実際の計算を実行しヒートマップを得る
cmap_out = gradient_function(prepro_input)
grad_CAM_map = cmap_out[0]
最終的に得られるgrad_CAM_mapがヒートマップです。
これをもとの入力画像サイズに引き伸ばして、入力画像と重ねることで、どの部位を見ているのかという可視化になります。
4.可視化例
可視化を実施してみます。
ちなみに、Grad-CAMに比べると圧倒的に処理時間が長くなります。PoI配列分の計算が増えるためと思います。
まず、前線検出された実例(出力層のセグメンテーション結果)を説明します。
4.1 自動描画された前線例
このデータは2017年3月22日UTC0時のデータでセマンティックセグメンテーションにより前線描画したものです。
気圧図を見ると、関東の東、東経149度北緯35度付近にピンク色で示される閉塞前線を伴う低気圧が見えており、閉塞点から南東方向に温暖前線(赤)、南から南西方向へ弧状に寒冷前線(青)が検出されています。比較的うまく前線が検出されている例です。
また、この低気圧のすぐ上には赤い「低」のような文字が出現しています。
さらに北海道付近にひとつ、他にもいくつかの「低」マークと、朝鮮半島付近に青い「高」の文字が見られます。
この時の正解ともいうべき、実際の気象図(SPAS)は下のようでした。
さきほどの自動検出結果と比べると、本物の方は寒冷前線が南西方向により長く引かれています。また閉塞点の位置もややずれているかと思われます。
低気圧マークは低気圧本体中心付近と北海道付近のものは合格圏内?その他は実際には解析されておらず、CNNは何を見て書きたくなったのか謎です。朝鮮半島付近の高気圧マークはまあ良いのではないかと思われます。
4.2 拡張版Grad-CAM++による可視化例
この前線を描画するためにニューラルネットワークが入力データのどういったところに着目したのかを今回拡張したGrad-CAM++により見ていきます。
(1)ニューラルネットワークの構造
各convolution層の上に書かれている数字が、conv2d_NNという層のNNを表しています。
以後の説明では、conv2d_NNで得られたヒートマップというような言い方をします。
(2)着目したconvolution層のヒートマップ全体像
まずconv2d_12のヒートマップを見てみます。この層は64x64のサイズで入力画像256x256に対して縦横ともに4分の1になっています。チャネル数は54です。
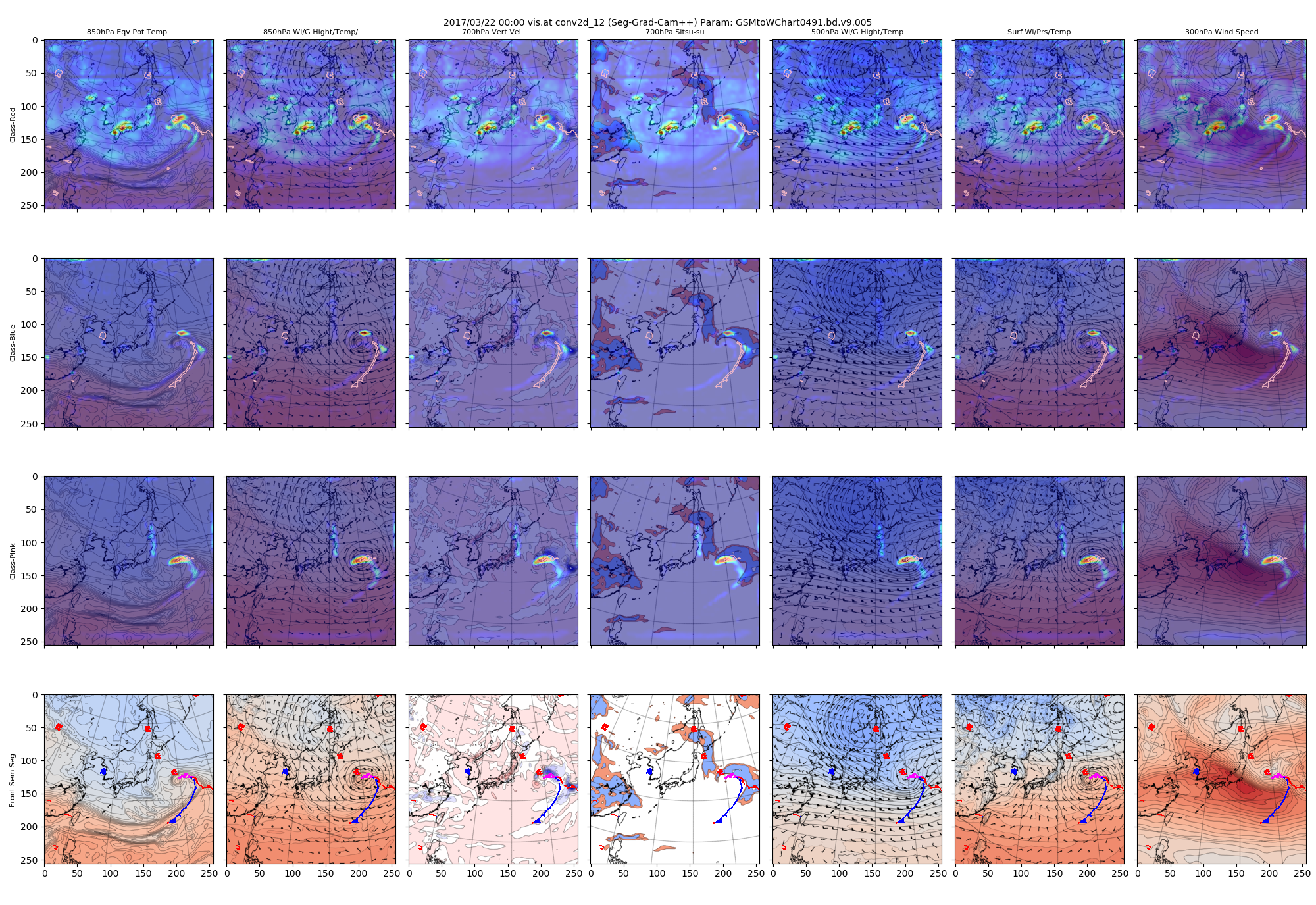
図 2017/3/22 conv2d_12で得られたヒートマップ(Grad-CAM++)
上記の絵は、上段から下に向かってクラス「1(赤)」「2(青)」「3(ピンク)」のヒートマップを、左から右方向に7種類の入力データのそれぞれにオーバレイして表示させたものです。3✕7=21種類の図になっています。
例えば上段の一番左側ですと、クラス「赤」のヒートマップを850hPa相当温位の図に重ねている状態です。
最下段には計算された前線と入力画像のオーバレイも表示しています。
ヒートマップ自体のカラーは、青色から黄色を経て赤色になるほど大きな値を示しています。
各クラスとも、低気圧の中心付近の構造を最も強く注視しており、それよりすこし薄い色ですが、前線構造をどこに描くかというような比較的おおきな構造も注視しているように見えます。
同じデータについて、Seg-Grad-CAM版を表示してみます。
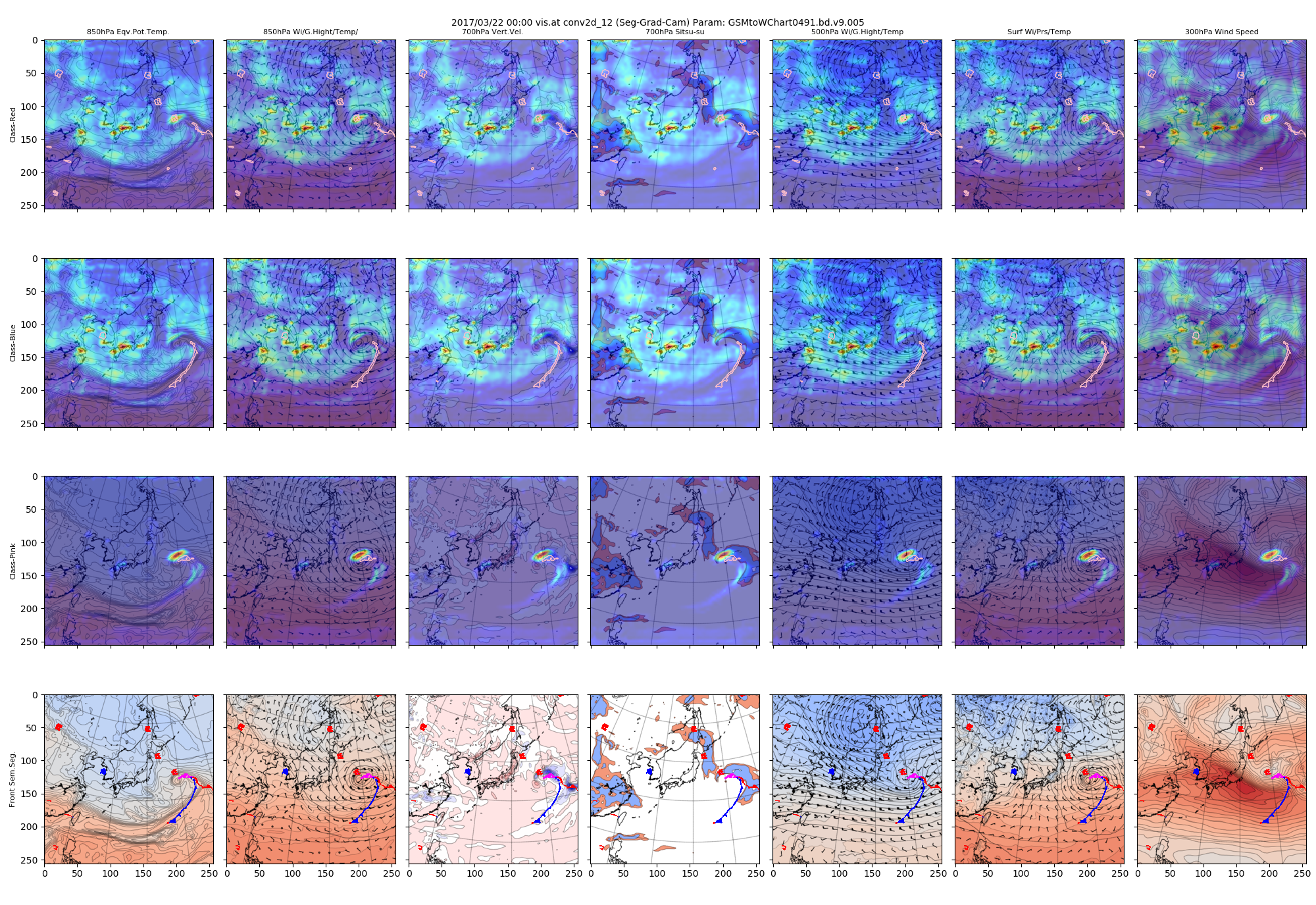
図 2017/3/22 conv2d_12で得られたヒートマップ(Grad-CAM)
Grad-CAM++版と比べると、クラス青とクラス赤の注視領域が広がっているように見えます。
ただし、他の層で得られたヒートマップを比較すると、Grad-CAM++とSeg-Grad-CAMの違いの傾向は層によって異なるようで一般的な傾向の説明は困難な印象です。
(3)深い層でのヒートマップ
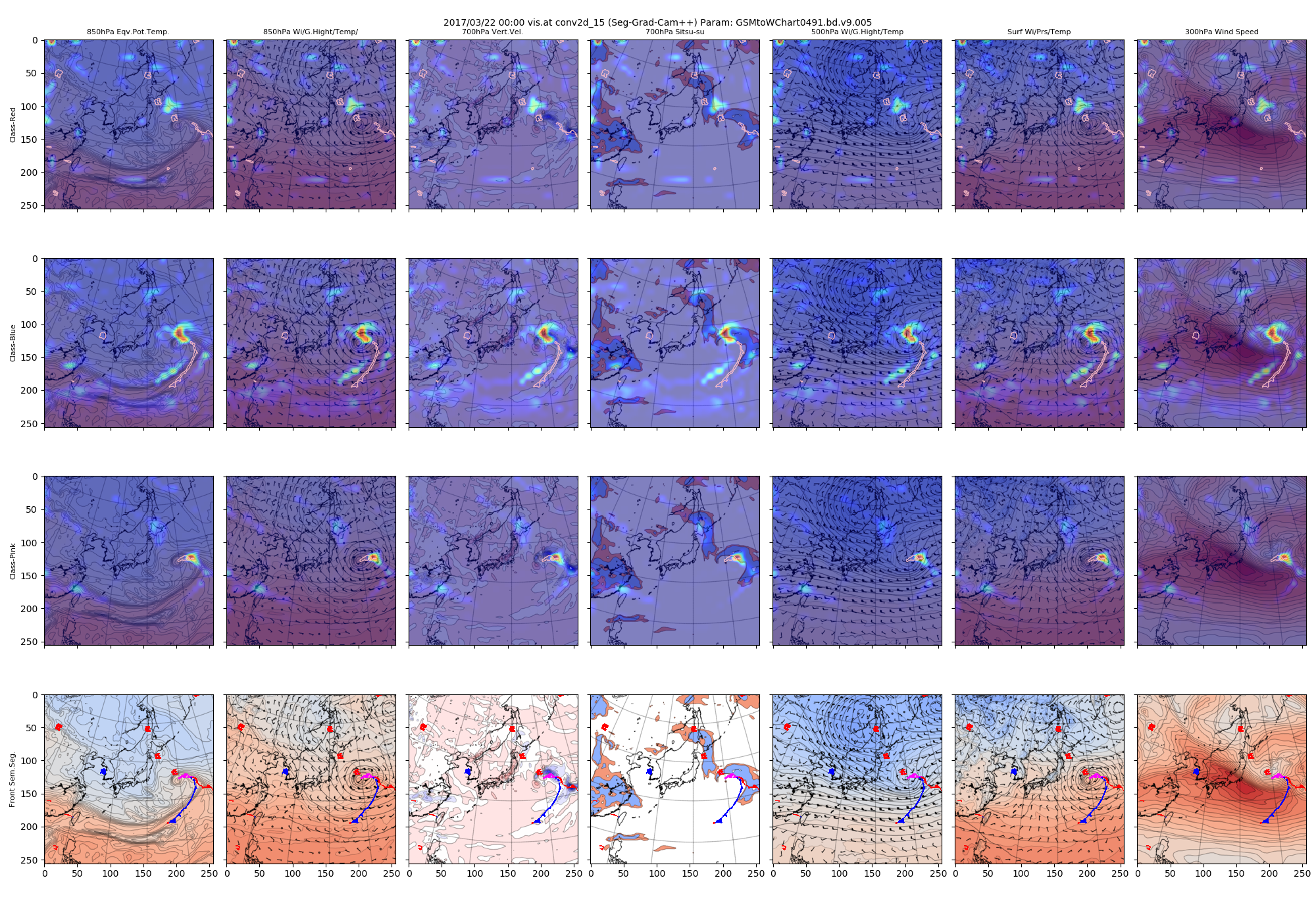
次に、もう少しネットワークの深い段階に進んだconv2d_15でのヒートマップです。
この層では画像サイズは32x32、80チャンネルになっています。
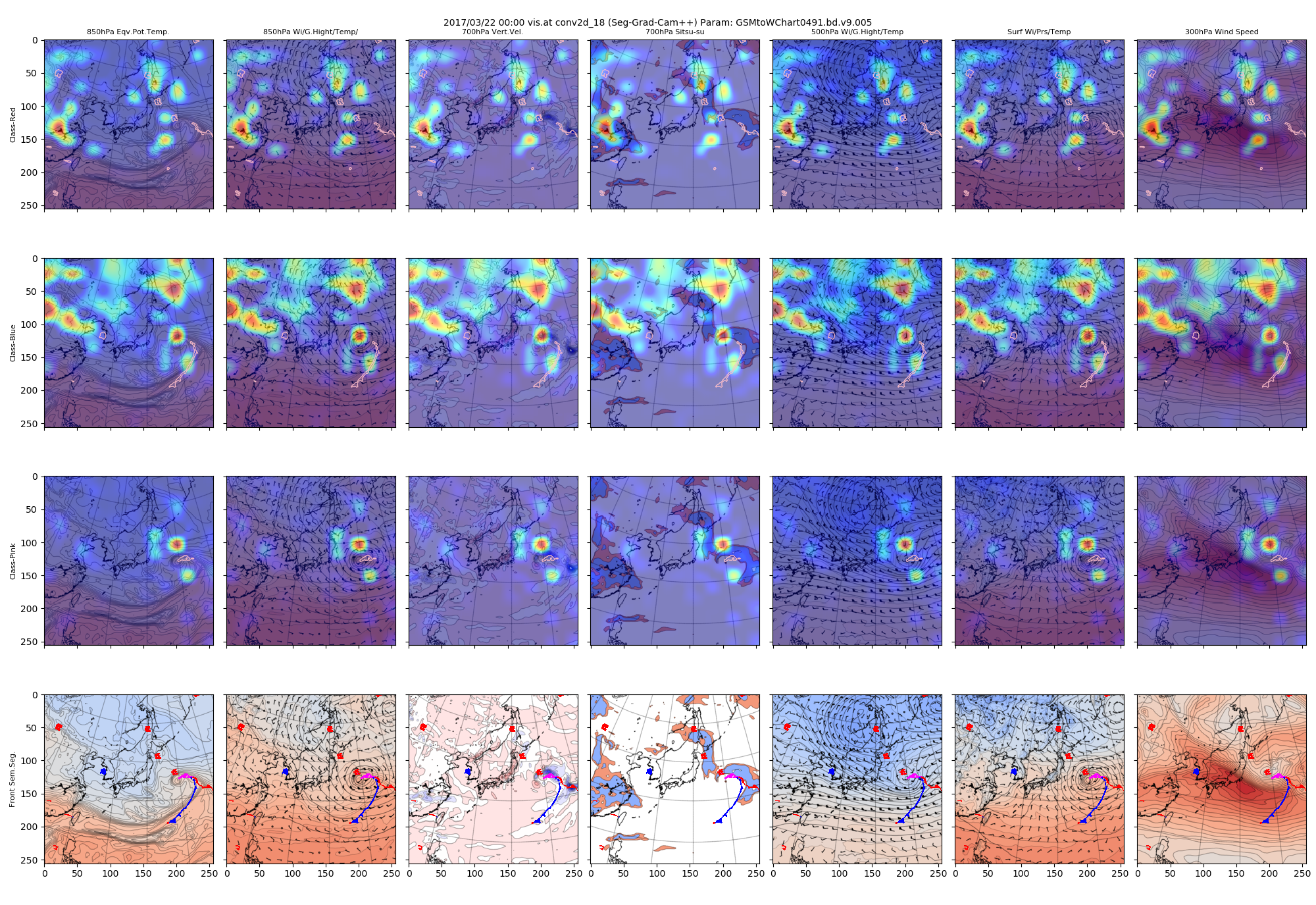
さらに進んだconv2d_17およびconv2d_18のヒートマップです。ここは画像サイズが16x16x120(ch)と最も抽象度が進んでいると考えられる、U-Netライクな構造のボトルネック部分になります。
深い層の可視化を見ると、低気圧の構造を細かく見ているようにも、低気圧や高気圧といった小さなものをどう描くかを見ているようにもみえます。
ピクセルごとのヒートマップを足し合わせているので、もう少し関心ある領域を絞った可視化をしてみるとどうなるかが気になります。
4.3 出力画像の一部領域に絞ったヒートマップ
勾配計算させる際に最終結果のピクセル範囲を、興味のある範囲に限定することで、前線や記号の影響の分離を試みます。
先に示したソースで、roibを有効にする_llc_x, _llc_y, _ruc_x, _ruc_yを指定します。
(1)前線と高気圧記号
クラス「青」について、関東の東にある低気圧の寒冷前線の部分、朝鮮半島付近にある高気圧記号、それぞれのみを使用してヒートマップを作成しました。指定した部分は緑色の矩形で示しています。矩形領域に含まれないクラス「赤」やクラス「ピンク」はヒートマップに表現されなくなります。
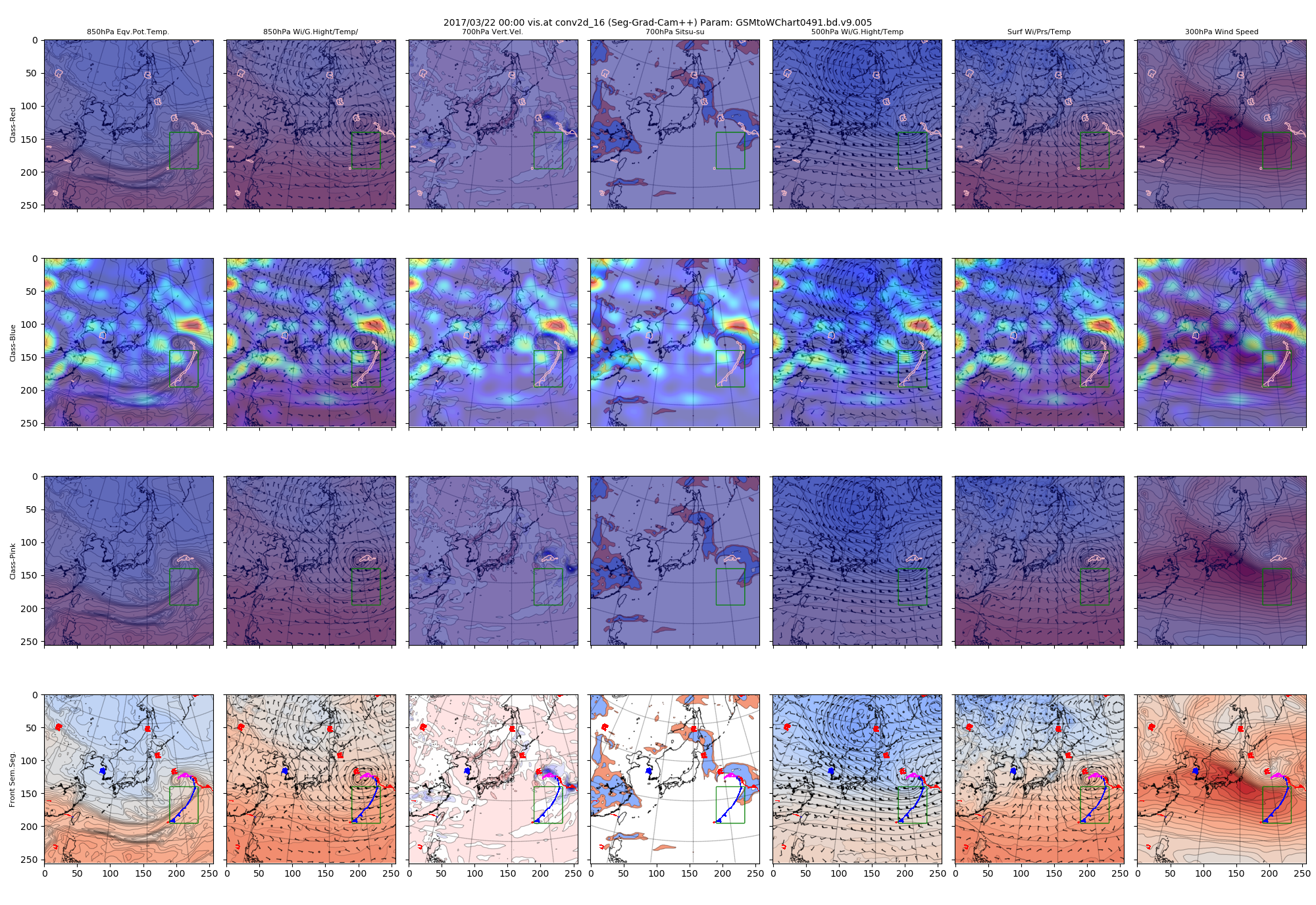
図:寒冷前線部分に絞ったヒートマップ(conv2d_16で得られたヒートマップ)
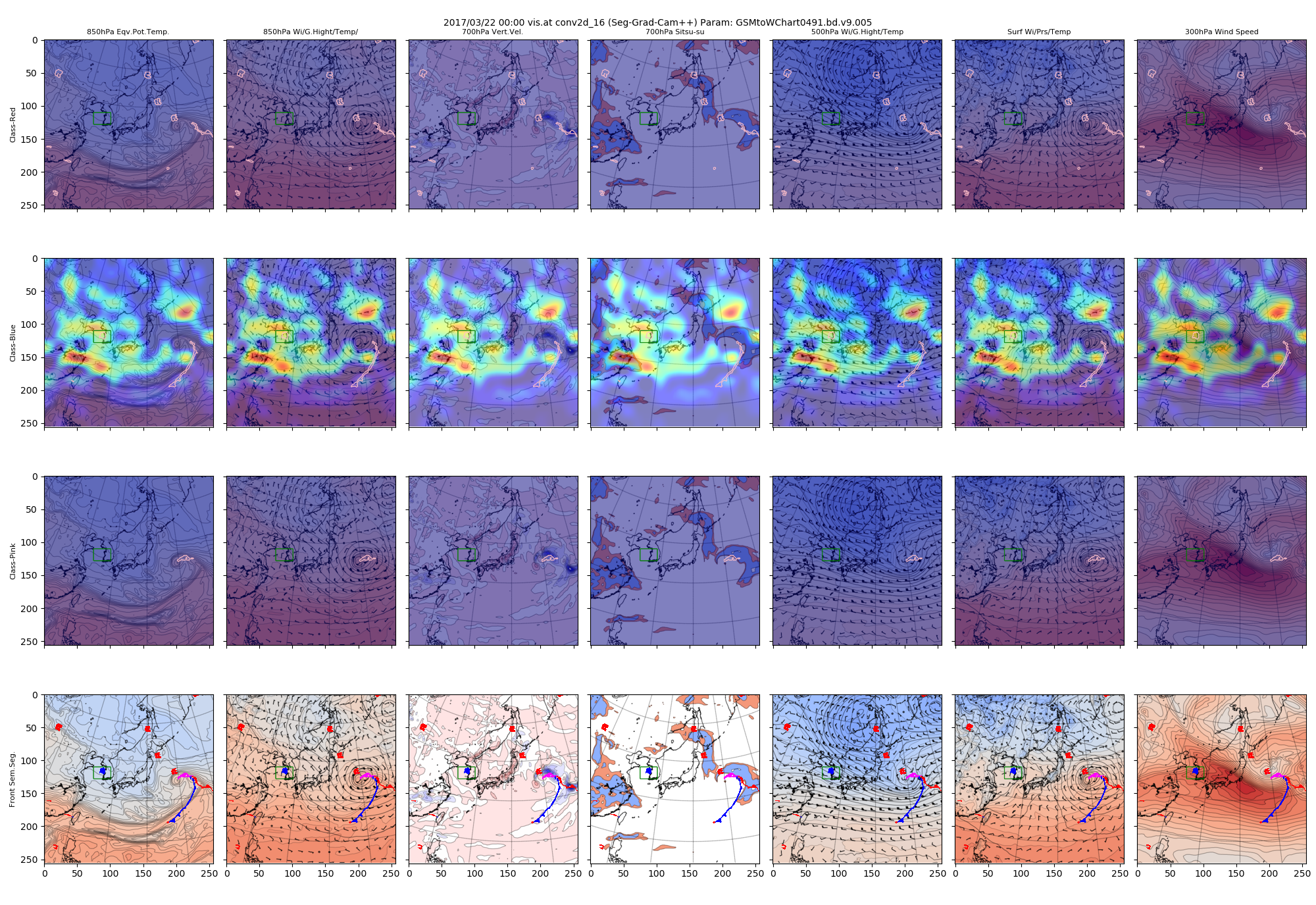
図:高気圧記号部分に絞ったヒートマップ(conv2d_16で得られたヒートマップ)
高気圧記号に絞った方は低気圧から西側の気象場の構造を全体的に捉えようとしているようにも見えます。
これに対して前線記号に絞った側は、低気圧周辺の等値線の集中しているところに注視しているようです。
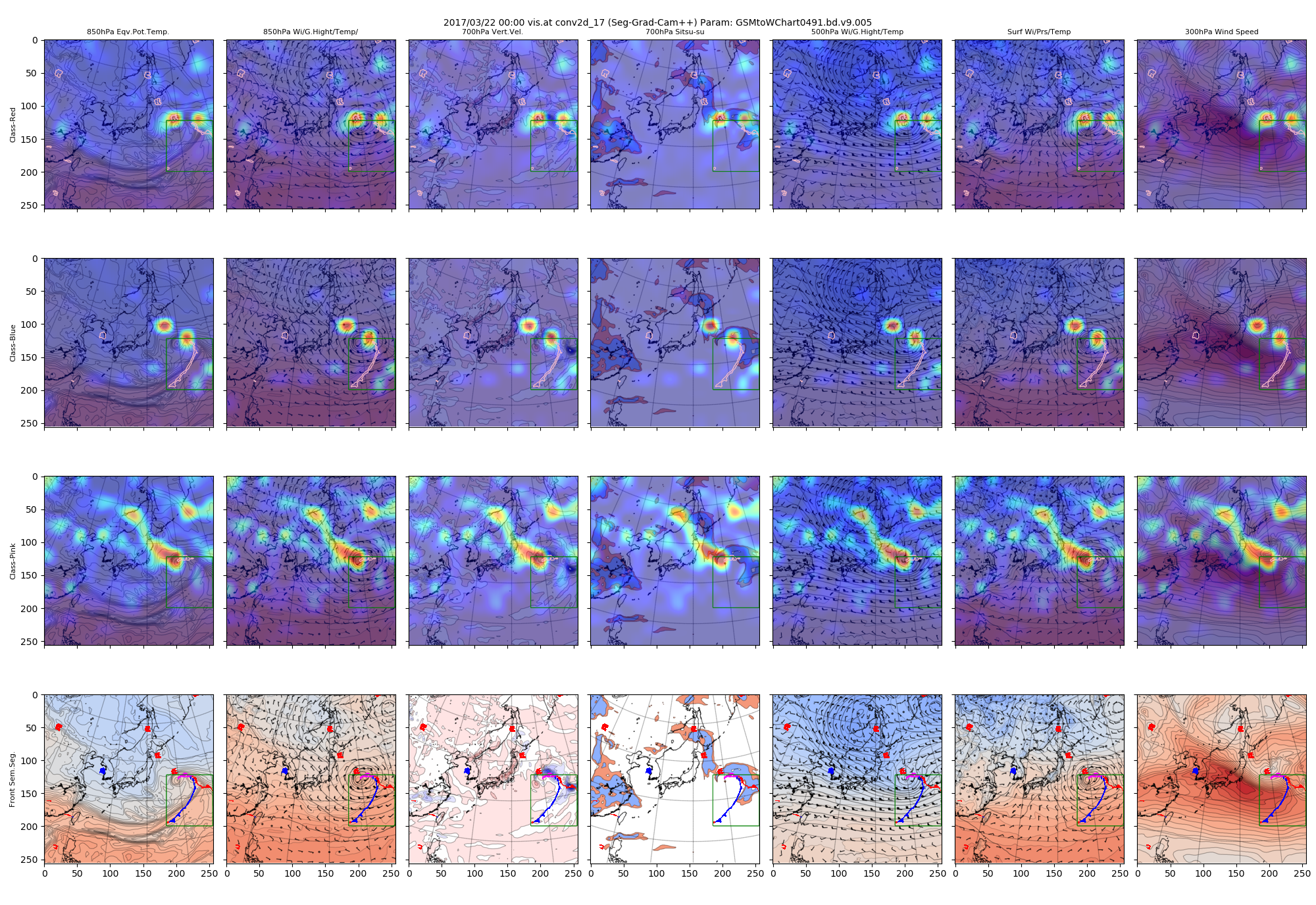
(2)低気圧に関わる前線に絞ったヒートマップ
高気圧や低気圧マークの影響を排除するため、関東東海上の低気圧の前線に絞ったヒートマップを作成してみます。
図:低気圧に関わる前線に絞ったヒートマップ(conv2d_17で得られたヒートマップ)
これを先ほどの、すべてのピクセル値を使用した前線に絞らないヒートマップと比較してみます。
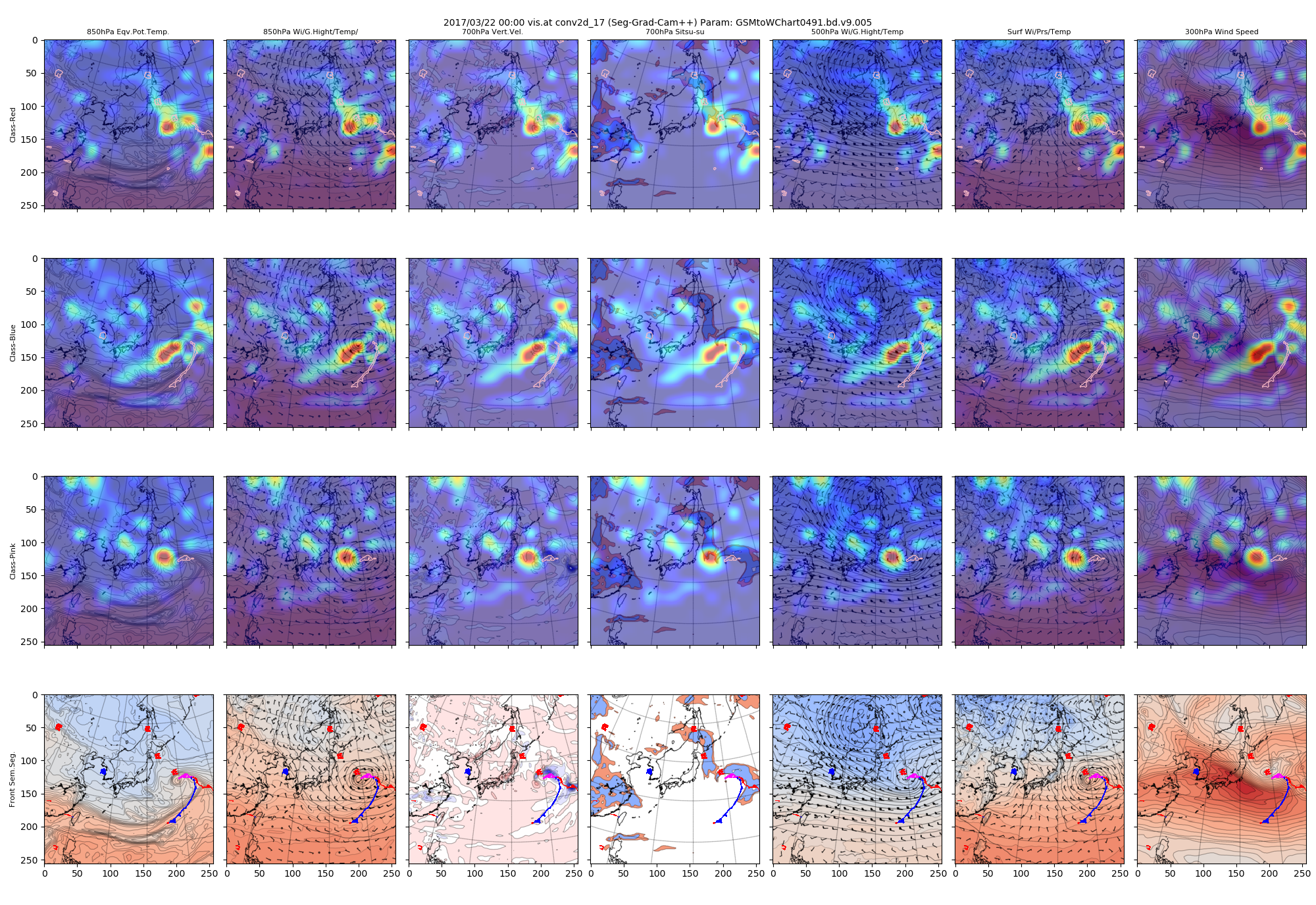
図:conv2d_17で得られたヒートマップ
絞った方は、クラス「赤」とクラス「青」は前線付近に注視領域が集中しました。
これは、低気圧記号や高気圧記号描画のために注視していた領域が減ったためと思われます。
また、クラス「ピンク」についても変化が大きいです。低気圧記号を含まないような矩形領域切り取りのために、前線の北側の一部が範囲外になってしまった影響と思われます。
これくらいの変化でも、ヒートマップへの変化が大きいということは、Grad-CAM系技術のセマンティックセグメンテーションへの適用の難しさを示しているのかもしれません。興味ある領域を絞りながら根拠を見ていく必要性が大きいと考えられるためです。
5.終わりに
5.1 まとめ
実施したこと:
Grad-CAM++をセマンティックセグメンテーションに拡張して実装しました。
これを用いて前線検出のCNNの注視領域の可視化を試みました。
感想:
Seg-Grad-CAMについても言えますが、関心領域の影響を見るにはなるべく範囲を絞った方が解釈しやすくなると思います。これは計算速度の問題からも、特にGrad-CAM++は処理量が大きくなっているので必要な方法です。
Grad-CAMと比べての優劣は、もう少し色々な例を可視化してみる必要がありそうです。
時間があれば、比較結果等を更新してみたいと思います。
疑問としては、数学的にYをAの線形結合で表しておきながら、YとSの非線形な式を利用して、線形結合の重みを導出しているようなところが気になりました。
5.2 前線に絞った学習
さらに、気象予報士としては色の違いでクラス化するのではなく、寒冷前線、温暖前線といった前線種別でクラス分けを行う方が適切だなと思うに至りました。色の違いでは、停滞前線を区別していないことになりますし、Grad-CAMの解釈としても気象状況との比較としては微妙に変なことをしているように思えてきます。
この問題については、カラー版のSPASから色で抽出して教師データを作成するのではなく、SPASのSVG版から教師データを作成する方法を試し始めています。
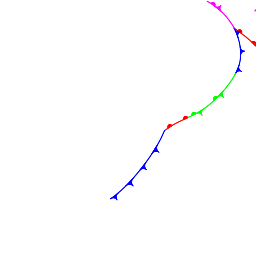
図:前線種別の色分けをした教師データ(赤:温暖前線、青:寒冷前線、ピンク:閉塞前線、緑:停滞前線)
さらに、前線記号の有無も変化をつけることが出来ます。
気象学的には、純粋に色分けされた曲線だけで行うことが適切に思えます。
しかし画像処理的には、前線記号があったほうが良い結果が得られる可能性もあると思いますので、どうなるか興味が湧いてきます。データを蓄積して、結果を見てみようとおもいます。
長文乱文をお詫びします。お読みいただいた方どうも有難うございました。
6. 参考
Seg-Grad-CAM
原論文
Towards Interpretable Semantic Segmentation via Gradient-weighted Class Activation Mapping, Kira Vinogradova, Alexandr Dibrov, Gene Myers
Grad-CAM++
原論文
Grad-CAM++: Improved Visual Explanations for Deep Convolutional Networks, Aditya Chattopadhyay, Anirban Sarkar and Vineeth N Balasubramanian。
解説記事
最新手法!「Grad-CAM++」のレビューと実装
Grad-CAM、Grad-CAM++、Score-CAMを実装・比較してみた
Grad-CAM++のオリジナル版の実装(Github)
adityac94/Grad_CAM_plus_plus