今回は、パラメータ更新を効率的に行う最適化について触れていきます。
\def\textlarge#1{%
{\rm\Large #1}
}
\def\textsmall#1{%
{\rm\scriptsize #1}
}
確率的勾配降下法（SGD）
これまで扱ってきた方法ですが、改めて記載すると以下のような内容でした。
Lは交差エントロピー誤差です。
ω \Leftarrow ω-\eta\frac{\partial L}{\partial ω}
学習率ηを作用させ勾配∂L/∂ωの逆方向にパラメータを変化させる、シンプルなアルゴリズムでした。
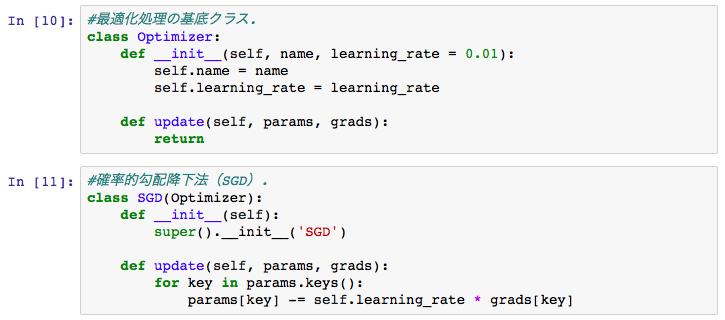
コードを記載します。
今回、いくつかパラメータの更新の最適化をトライするため、基底クラスでOptimizerというクラスを用意します。
手法名と共通の学習率を保持し、パラメータのアップデートを行う「update」関数を保有する簡単なクラスです。
それを派生して勾配法のクラスを用意します。
学習率は、前回から値を小さくし0.01。
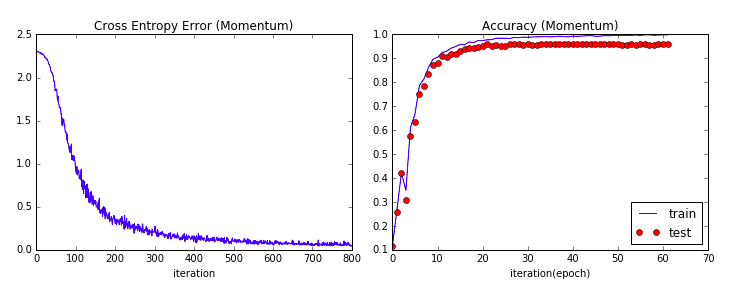
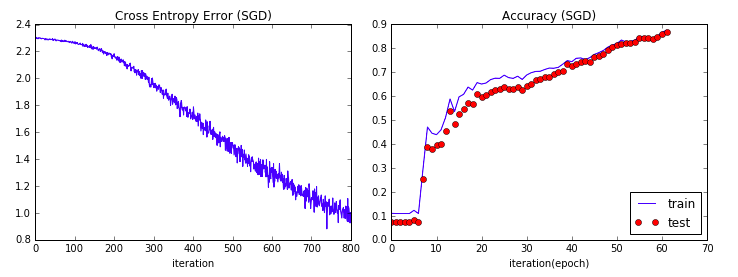
繰り返し回数を800回で設定したときの交差エントロピー誤差の推移と
精度の推移は以下のようなグラフになります。
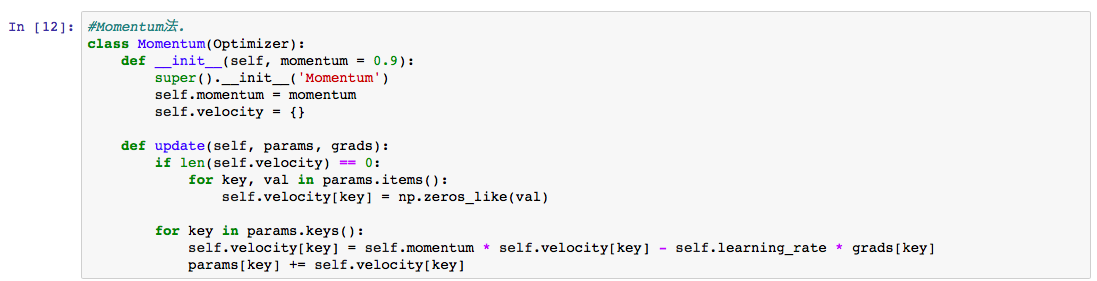
Momentum法
パラメータの最小値を物理法則的なアプローチで解析する手法です。
ちなみにMomentumは運動量という意味です。
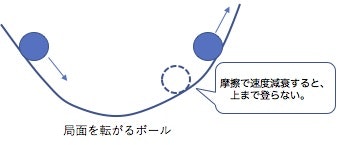
パラメータが作り出す空間局面をボールが転がって、凹みの極値にたどり着くイメージを考えます。
局面に摩擦があると、速度が減衰する分、余計な振れ幅がなく早く極値に達するようなモデルになるかと思います。
数式で記述すると、このような形です。
v \Leftarrow αv-\eta\frac{\partial L}{\partial ω}\\
ω \Leftarrow ω+v
上記のvは速度に対応します。
αは１より小さい正の値で、速度減衰のパラメータです。
Momentum法のクラスコードを記載します。
減衰率は0.9としています。
先ほどのSGDと合わせてグラフを表示してみます。
上がMomentum、下がSGDです。
Momentum法が早く極値に近づいていることがわかるかと思います。
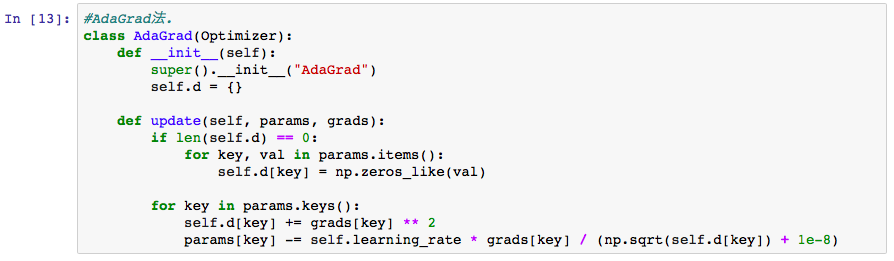
AdaGrad法
先ほどのMomentum法の例のように、ボールが局面を転がるときは、凹みの極値に近づくほど、ボールの振れ幅を少なくなるように調整できれば、早く結果に辿りつきそうです。
AdaGrad法はそのようなモデルのアルゴリズムです。
数式を記載します。
D \Leftarrow D+\frac{\partial L}{\partial ω}◦\frac{\partial L}{\partial ω}\\
ω \Leftarrow ω-\frac{\eta}{\sqrt{D}}\frac{\partial L}{\partial ω}
「◦」の演算は行列の対応する要素ごとの乗算（2乗値）になります。
ステップが進むとDの値は大きくなるため、パラメータの変動が小さくなることがわかるかと思います。
AdaGrad法のクラスコードを記載します。
先ほどのMomentumと合わせてグラフを表示してみます。
上がAdaGrad、下がMomentumです。
交差エントロピー誤差については、AdaGradの初期減衰のスピードが早いですが、後半はMomentumの方が良い数値になっています。
一方、精度（Accuracy）については、AdaGradの方が早い段階で高い精度に近づいていることがわかるかと思います。
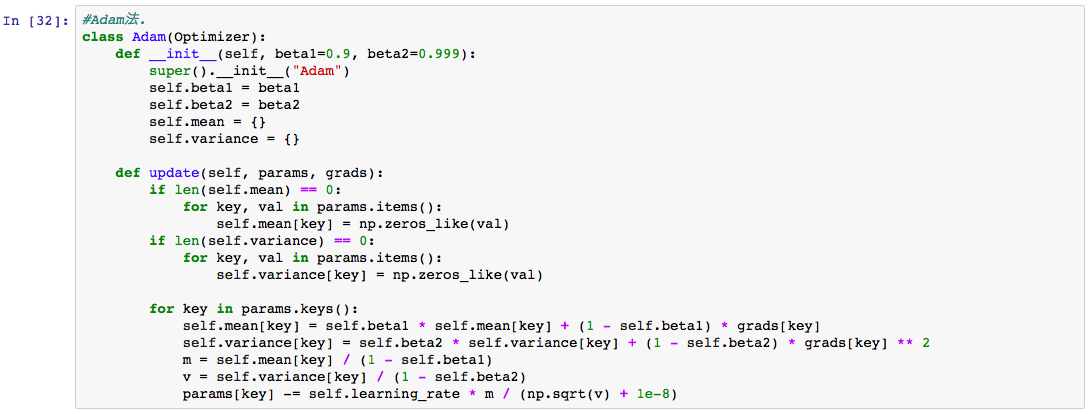
Adam法
最後にAdam法を紹介します。
上記のMomentum法とAdaGrad法を融合したような方法と言われています。
詳しい説明は省略いたしますが、原文はこのサイトにあります。
こちらのサイトにechizen_tmさんがわかりやすく説明した資料があります。
コードを記載します。
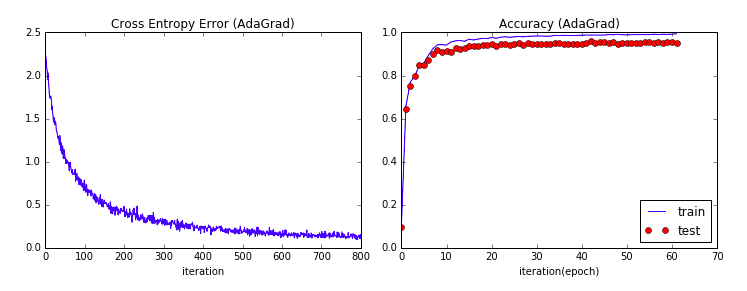
交差エントロピー誤差と精度の推移は以下のようなグラフになります。
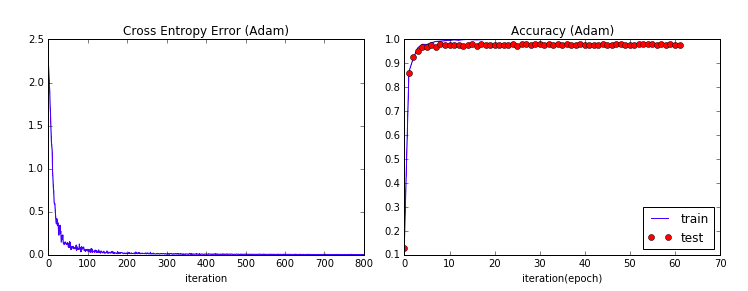
交差エントロピー誤差の減衰スピード、Accuracyの立ち上がりスピードも非常に早いことがわかるかと思います。
今回は、パラメータ更新の最適化について紹介いたしました。
Momentum法、AdaGrad法、Adam法を用いれば、繰り返し頻度を下げることができ、解析のパフォーマンスアップに繋げることができます。
今回はここまで。