今回は、さらにパラメータ更新のスタート段階の、重みの初期値に着目します。
初期値を変化させることで、交差エントロピー誤差の収束スピードがどのような変化をするのかを、プログラムで確認していきます。
\def\textlarge#1{%
{\rm\Large #1}
}
\def\textsmall#1{%
{\rm\scriptsize #1}
}
初期値の取り方による学習推移の変化
プログラムは、現在以下のような形になっています。
隠れ層にそれぞれ、正規分布での乱数に0.01の係数で重み付けをしています。
この係数を、1.0, 0.1, 0.01, 0.001の4パターンで変化させた時の、
交差エントロピー誤差と、精度の変化をグラフで表示してみます。
OptimizerはシンプルなSGD（勾配法）を用います。
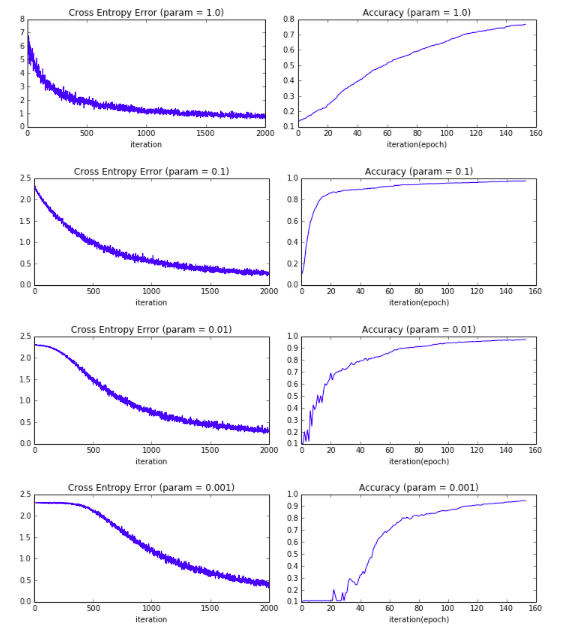
以下のような変化をします。
グラフのタイトルの「param=***」が係数に該当します。
グラフを見ていただくと、係数が大きいほど交差エントロピー誤差の減衰スピードは
早くなっています。
一方、Accuracy（精度）を見てみると、係数が大きい1.0の場合は
精度の向上スピードは緩やかです。
また、逆に係数が小さい0.001の場合については、精度向上の立ち上がりが遅れており
こちらもあまり良い結果とは言えません。
交差エントロピー誤差の減衰、精度向上の推移でバランスが良いのは
この場合ですと、係数が0.1の場合になるでしょう。
このように、パラメータの初期値をどのように設定するかで、
学習のスピードが大きく変わってくるのが分かるかと思います。
Xavierの初期値
上記では、係数を定数値で変化させて学習の推移を見ましたが、ロジック的には
どの層にも同じ係数を掛ける処理を行っていました。
次に紹介する、「Xavierの初期値」は層のノードの数によって、作用させる係数を
変化させます。
たとえば、前層から渡されるノード数がn個であるときには、標準偏差√nで割ってやります。
つまり以下の値を作用させます。
\frac{1}{\sqrt n}
つまり、初期値のバラツキについては、各層ごとにノードの数で均一化しているイメージになるかと思います。
初期値の重み付けのコードは、単純に以下のように変化します。
係数として、重み付けを定数で0.1を作用させた場合と、Xavierの初期値を用いた場合を比較してグラフ化してみます。
以下のような推移となりました。
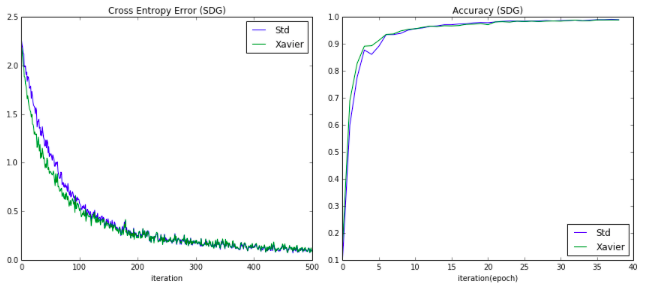
青線が定数0.1の初期値重み、緑線がXavierの初期値です。
ほとんど推移は変わりませんが、若干Xavierの方が学習推移が早い結果となりました。
Heの初期値
Xavierの初期値と共によく使われる初期値として「Heの初期値」があります。
作用させる値はXavierと似ていますが、標準偏差√(n/2)で割ってやります。
つまり以下の値を作用させます。
\sqrt\frac{2}{n}
これまで、活性化関数はSigmoid関数を用いていました、Heの初期値は
活性化関数は、ReLU関数と一緒に使用します。
ReLU関数は今まで触れておりませんでしたが、以下のようなシンプルな関数です。
f(x)=max(0,x)
つまり、xが0以下の値のときは0, xが正の値の場合はそのままxの値をとる関数です。
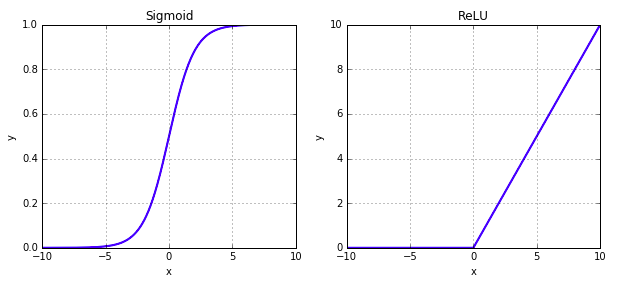
Sigmoid関数の形を見ると、(x,y) = (0, 0.5)を中心に点対称のグラフです。
それに比べて、ReLu関数は負の数は0で丸められ、同時に負の領域では値のバラツキは0になります。
Heの初期値がReLU関数を採用し、値のバラツキの分散値を半分の値にしているのも、
活性化関数の形から直感的にわかるような気がします。
また、ReLU関数についての、バックプロバケーションのクラスは以下のようなコードになります。
また、ニューラルネットワークのクラスも、初期値を3パターン（定数0.01, Xavier, He）で設定できるように拡張します。
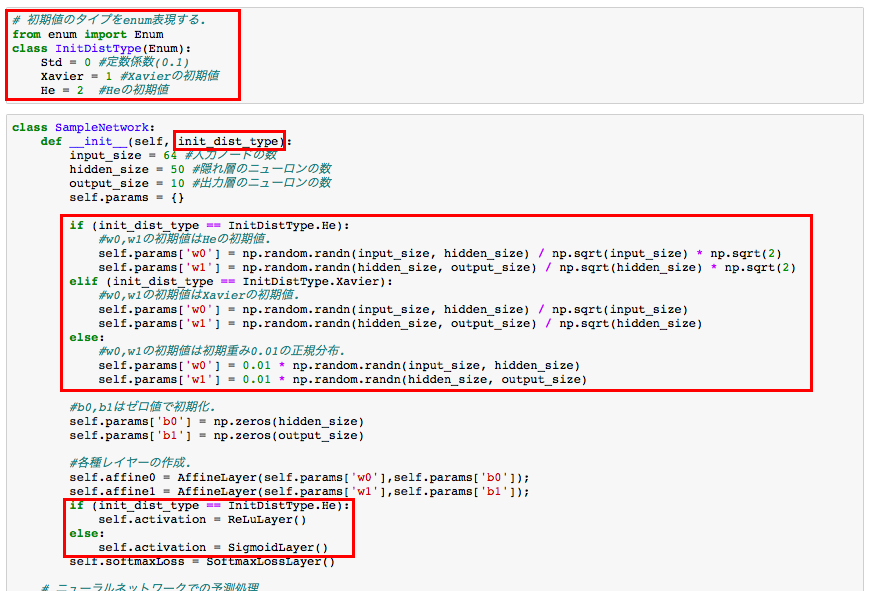
それぞれの、初期値でグラフを出力すると、以下のような結果になりました。
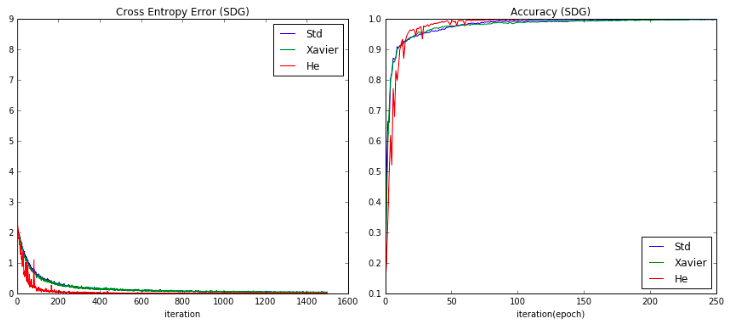
青線の定数0.1（Std）の重み付けの推移と、緑線のXavierの初期値での推移は
結果的に大きな差はありませんでしたが、
赤線のHeの初期値の採用したものは、交差エントロピー誤差の減衰スピードが
他のものより早い結果が得られました。
ただ、Heの場合は活性化関数でReLUを採用した影響なのか、グラフの推移の振動幅が
大きいという特徴も見られます。
以上、今回はここまで。