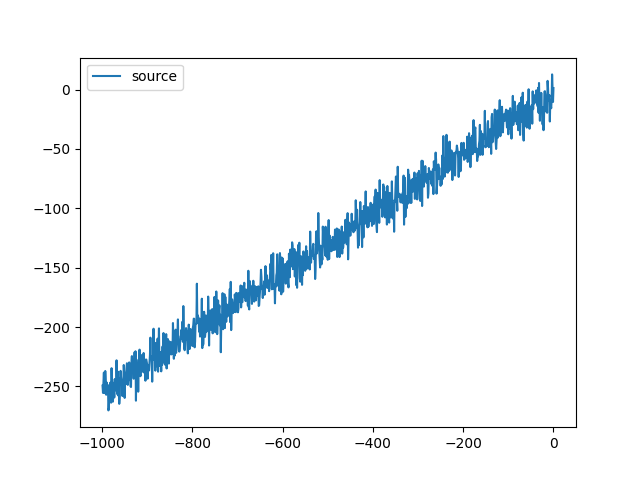
仮想通貨取引botのロジックを組んでいるとトレンド(傾向)の影響を取り除いたボラリティ(価格変動)を求めたい場合がある。
価格の上昇傾向・下降傾向といったトレンドを一次式で表せると仮定して、その推定した一次式の残差の標準偏差をボラリティの度合いとしてみなすことができる。
価格推移は連続しているのでこのようなグラフにはならないが、目をつぶってこのデータを用いるとして残差分散を求める。以下にコードを示す。
import numpy as np
import matplotlib.pyplot as plt
def generate(a, b, c, n=1000):
np.random.seed(9)
print("傾き {}, 切片 {}, 誤差分散 {}".format(a, b, c ** 2))
x = np.arange(n) - n + 1
y = a * x + b + c * np.random.normal(size=n)
return x, y
def regression(x, y):
cov = np.cov(x, y)
Sxx, Sxy, Syy = cov[0, 0], cov[0, 1], cov[1, 1]
# assert Sxx == np.var(x, ddof=1) # same value, unbiased variance
# assert Syy == np.var(y, ddof=1) # same value, unbiased variance
a, b, c = Sxy / Sxx, np.mean(y) - Sxy / Sxx * np.mean(x), np.sqrt(Syy - Sxy ** 2 / Sxx)
print("傾き(推定) {}, 切片(推定) {}, 残差分散 {}".format(a, b, c ** 2))
return a, b, c
def main():
fig = plt.figure()
ax = fig.add_subplot(111)
x, y = generate(0.25, -4.5, 10)
ax.plot(x, y, label="source")
a, b, c = regression(x, y)
ax.plot(x, a * x + b, label="regression")
ax.plot(x, a * x + b + c * np.sin(x / len(x) * 100), label="regression+$1\sigma$")
ax.legend()
plt.show()
if __name__ == "__main__":
main()
# output
# 傾き 0.25, 切片 -4.5, 誤差分散 100
# 傾き(推定) 0.24944011563873922, 切片(推定) -4.463923597333633, 残差分散 103.9897989356159
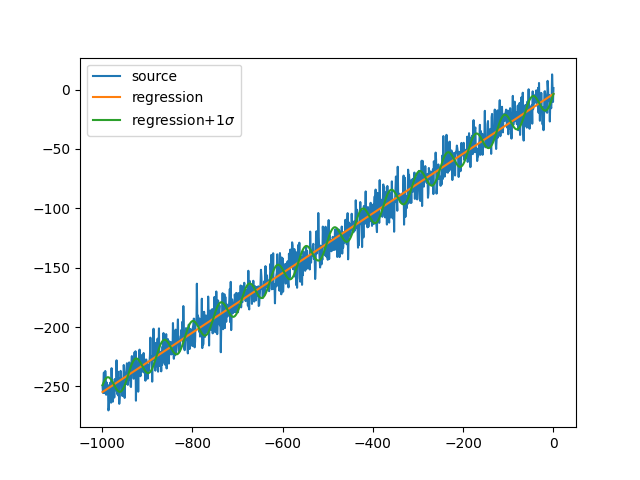
上の出力画像は推定した残差分散の平方根で標準偏差を得てsin波の振幅で表現している。
関数regression(x, y)から分かるように残差分散$S_{ee}$を求めるのに推定値との残差を求めて分散を取る必要はない。
$S_{xx}$:xの分散, $S_{yy}$:yの分散, $S_{xy}$:xyの共分散が求まっていれば$S_{ee}=S_{yy}-\frac{S_{xy}^2}{S_{xx}}$で求まる
$\hat{y}=a\hat{x}+b$ という回帰式は傾きが$a=\frac{S_{xy}}{S_{xx}}$で切片が$b=\overline{y}-a \overline{x}$なので
残差分散$S_{ee}$は定義通り計算すると$\frac{1}{n}\sum (ax+b-y)^2$だが以下のように分散・共分散だけの式に整理することができるためである。
$S_{ee}=\frac{1}{n}\sum (ax+b-y)^2=\frac{1}{n}\sum (\frac{S_{xy}}{S_{xx}}(x-\overline{x})-(y-\overline{y}))^2$
$\frac{S_{xy}^2}{S_{xx}^2} \frac{1}{n}\sum (x-\overline{x})^2-2\frac{S_{xy}}{S_{xx}}\frac{1}{n}\sum(x-\overline{x})(y-\overline{y})+\frac{1}{n}\sum(y-\overline{y})^2=\frac{S_{xy}^2}{S_{xx}}-2\frac{S_{xy}^2}{S_{xx}}+S_{yy}=S_{yy}-\frac{S_{xy}^2}{S_{xx}}$
共分散行列でnp.cov(x,y)が$\begin{bmatrix} S_{xx} & S_{xy} \\ S_{xy} & S_{yy} \end{bmatrix}$を返すので$S_{ee}=S_{yy}-\frac{S_{xy}^2}{S_{xx}}$はすぐ求まる。ただnp.cov(x,y)の返す値は全て不偏分散であるため残差も不偏分散である点には注意。