応用情報技術者平成30年秋期 午前問8
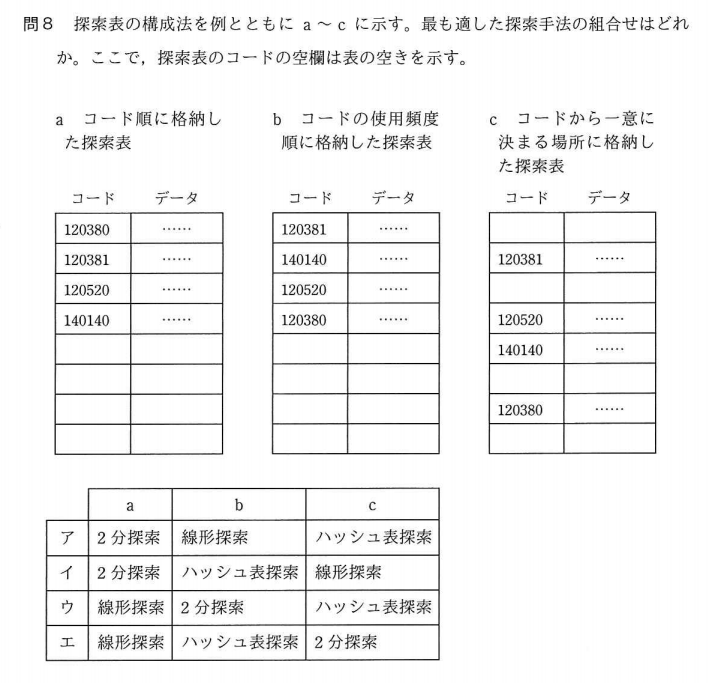
探索表の構成法を例とともに a~c に示す。探索の平均計算量が最も小さい探索手法の組合せはどれか。ここで,探索表のコードの空欄は表の空きを示す。
探索表を平均計算量が最も小さいの手法ですね。
データの特性を確認するのは必要ですね。
aは整列済とか、
bは使用頻度順で格納したとか、
cはコードから一意に決まる場所に可能した
ですね。この情報を利用して、最も小さい探索方法を決めますね。
[a コード順に格納した探索表]
探索表はコード順に整列済みなので、線形探索または2分探索を使用可能です。各探索法の平均探索回数は、線形探索が (N+1)/2 回、2分探索法が [log2N] 回ですので、探索表の要素数が同じならば平均探索回数は2分探索のほうが少なくて済みます。したがってa表には2分探索が適切です。(※[n]はnを超えない最大の整数を表します)
[b コードの使用頻度順に格納した探索表]
使用頻度が高いデータほど探索表の先頭のほうに位置していることになります。線形探索では探索表の先頭から順番に探索していくので、このような探索表に対しては効率的に探索できます。
2分探索法は、データが整列されていないと使えないという制限がありますし、この表はハッシュ法に対応していないので、b表に対しては線形探索が唯一使用できる方法となります。
[c コードから一意に決まる場所に格納した探索表]
ハッシュ法は、探索データのキー値から、そのデータの格納場所(アドレス)を直接計算する方法で、(シノニムが発生しなければ)1回の計算で一意に目的のデータにたどりつけます。
1回の探索でいいので、このc表に対して最も計算量が少なくなる探索法はハッシュ表探索です。