応用情報技術者平成30年秋期 午前問75
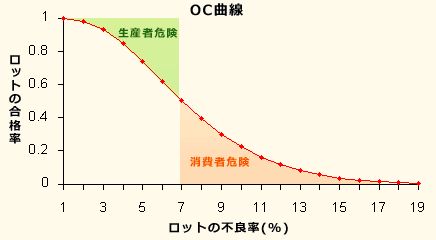
横軸にロットの不良率,縦軸にロットの合格率をとり,抜取検査でのロットの品質とその合格率の関係を表したものはどれか。
1、OC曲線(Operating Characteristic curve)は、ロットの不良率とそのロットの合格率の関係を表したグラフです。ロットの不良率がnである場合にロットの合格率が一意に決まることを表しています。
製品の抜き取り検査では、ロットからn個のサンプルをとり、それに含まれる不良品個数が c個以上であればそのロットを不合格とするという判定を行います。
OC曲線は、nおよびcを固定とした場合のロットの合格率(p)を縦軸に、実際のロットの不良率(q)を横軸に取り、pとqの関係を表した曲線です。
・本来合格となるべきロットが、抜き取り検査で不合格になってしまう確率を生産者危険、
・本来不合格となるべきロットが合格になってしまう確率を消費者危険
といいます。
・ロット:同じ条件のもとに製造する製品の、生産・出荷の最小単位。
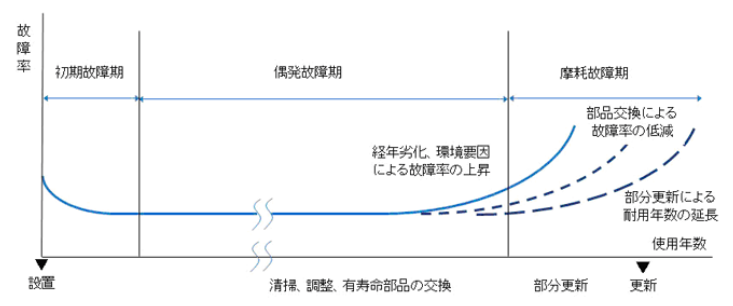
2、バスタブ曲線は、 bath-tub curve
故障率曲線とも呼ばれ、機械や装置の時間経過に伴う故障率の変化を表示した曲線です。
バスタブ曲線(故障率曲線)とは、時間が経過することによって起こってくる機械や装置の故障の割合の変化をしめすグラフのうち、その形が浴槽の形に似ている曲線のことです。
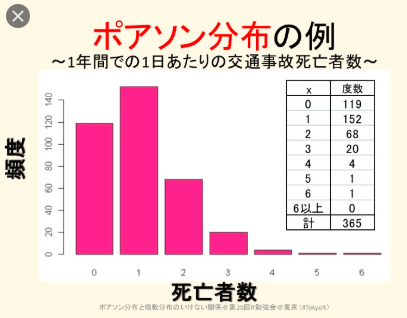
3、ポアソン分布は、
非常に大きな集団においてきわめて起こりにくい事象を対象としたときの分布です
統計学および確率論においてポアソン分布(英: Poisson distribution)とは、数学者シメオン・ドニ・ポアソンが1838年に確率論とともに発表した、所与の時間間隔で発生する離散的な事象を数える特定の確率変数 X を持つ離散確率分布のことである。ある離散的な事象に対して、ポアソン分布は所与の時間内での生起回数の確率を示し、指数分布は生起期間の確率を示す[1]。
ポアソン分布とは「一定時間内にランダムなイベントが何回発生するか」を表す分布です。
例えば「地震の発生回数」を「ランダムなイベント」とみなすと,「これから 100 年間のうちに地震が発生する回数」がポアソン分布で表現できます。
4、ワイブル分布は、
物体の体積と強度との関係を定量的に記述するための確率分布で、部品などの寿命特性を統計的に記述するために利用されます。
ワイブル分布(ワイブルぶんぷ、英: Weibull distribution)は、物体の強度を統計的に記述するためにW. ワイブル (Waloddi Weibull) によって提案された確率分布。 時間に対する劣化現象や寿命を統計的に記述するためにも利用される。
つまり、
・OC曲線:不良率/良率曲線
・ポアソン分布:発生確率分布
・バスタブ曲線:故障率曲線
・ワイブル分布:寿命特性/劣化現象統計分布
ですね。
参照:
https://www.ap-siken.com/kakomon/25_aki/q75.html
ポアソン分布
https://www.slideshare.net/teramonagi/ss-11296227
ポアソン分布
https://ja.wikipedia.org/wiki/%E3%83%9D%E3%82%A2%E3%82%BD%E3%83%B3%E5%88%86%E5%B8%83