度数分布表
度数分布表とは、収集した**「データの分布の状態」**(データの中心や散らばりの様子)を知るために、ある幅ごとに区切ってその中に含まれるデータの個数を見るために作成した表のことを言います。
まずは簡単な50個のデータ(単位:人)を準備します。
data1 <- c(67, 58, 75, 89, 46, 62, 56, 79, 60, 30, 76, 64, 52, 66, 42,
81, 63, 59, 65, 77, 38, 86, 64, 70, 50, 93, 78, 76, 57, 68, 98, 64,
55, 66, 53, 82, 62, 73, 60, 51, 49, 67, 56, 75, 85, 61, 58, 44, 79, 65)
data1より度数分布表を作成すると以下の通りになります。
| 階級(単位:人) | 階級値 | 度数 | 相対度数 | 累積度数 | 累積相対度数 |
|---|---|---|---|---|---|
| 30以上~40未満 | 35 | 2 | 0.04 | 2 | 0.04 |
| 40以上~50未満 | 45 | 4 | 0.08 | 6 | 0.12 |
| 50以上~60未満 | 55 | 11 | 0.22 | 17 | 0.34 |
| 60以上~70未満 | 65 | 16 | 0.32 | 33 | 0.66 |
| 70以上~80未満 | 75 | 10 | 0.20 | 43 | 0.86 |
| 80以上~90未満 | 85 | 5 | 0.10 | 48 | 0.96 |
| 90以上~100未満 | 95 | 2 | 0.04 | 50 | 1.00 |
各項目について説明していきます。
階級
度数を集計するための区間
適切な階級の数を設定するためには**「スタージェスの公式」**が用いられます。
k=1+log_2N
kは階級の数を表し、Nはデータの個数を表します。
正式な度数分布表の作成手順では、データの範囲(最大値-最小値)をスタージェスの公式で算出した階級の数で割ることで階級の幅を求めます。
今回は以下のように階級の幅を求めました。
範囲:98-30=68 階級の数:1+log_250=1+5.643…≒7
階級の幅:\frac{範囲}{階級の幅}=\frac{68}{7}=9.714…≒10
階級値
各階級の中央値であり各階級を「代表」する値
相対度数
度数を総度数(全データ数)で割った値
無作為に1つのデータを抽出する場合、相対度数はそのデータがある階級に属している確率と一致します。
累積度数
度数を小さい階級から累積した値
累積相対度数
累積度数を総度数で割った値
一番最後の階級の累積相対度数は1になります。
ヒストグラム
度数分布表を用いて、縦軸に度数・横軸に階級をとり、グラフ化したもの
カール・ピアソンによって用語が創案されました。
ヒストグラムの形状よりデータの分布の特徴を整理する時は、次の①~⑤のポイントに留意します。
① データの中心はどのあたりにあるか
② データの散らばりは大きいか・小さいか
③ 分布のピーク(頂上)はいくつ存在するか▶︎一様分布(ピーク0)・単峰性・二峰性・多峰性
④ データの分布は左右対称か▶︎右に歪んだ分布・左右対称な分布・左に歪んだ分布
⑤ 外れ値は存在するか
data1よりヒストグラムを作成すると以下の通りになります。
hist(data1, freq = TRUE, ylim = c(0, 20),
xlab = "人数",
ylab = "度数",
main = "ヒストグラム")
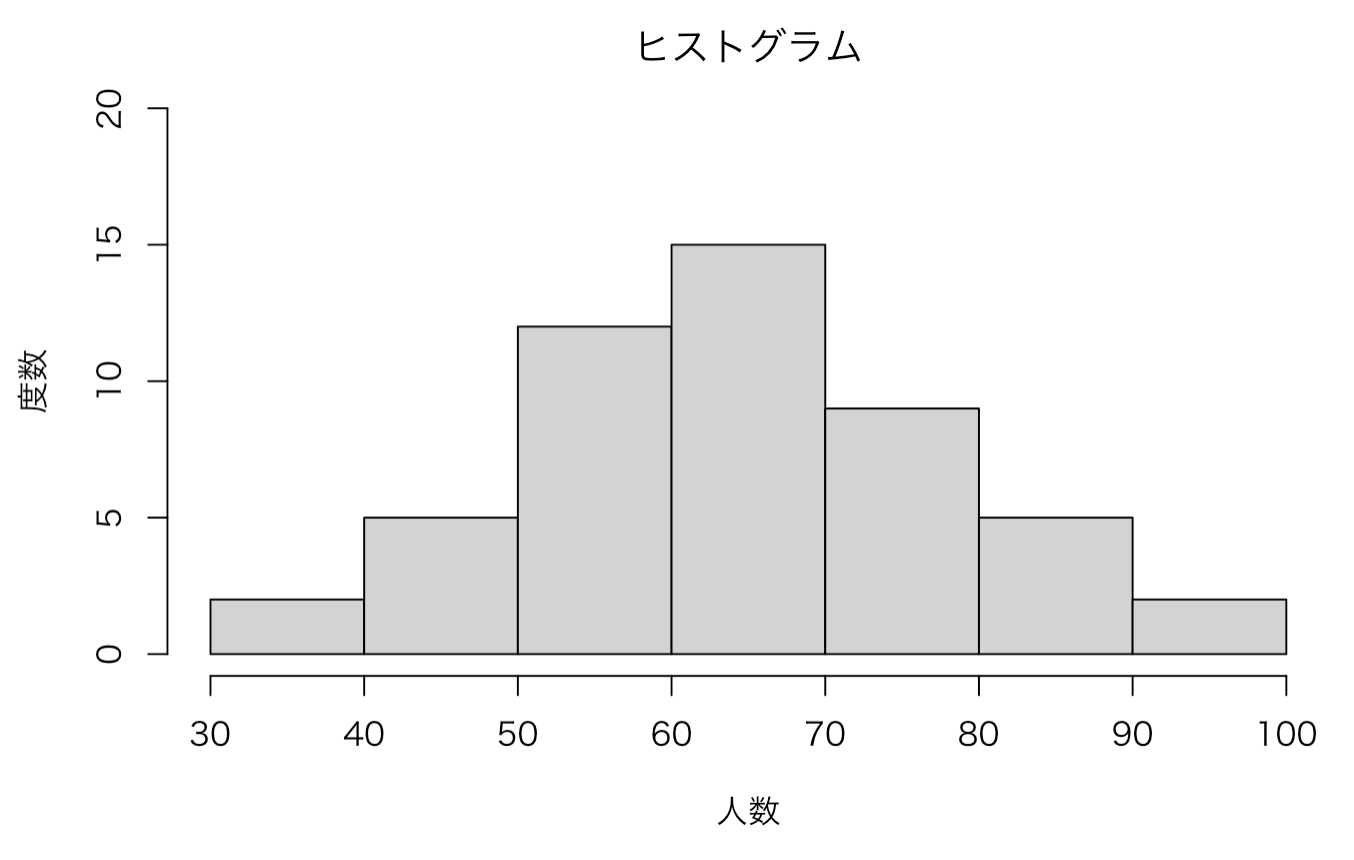
今回のヒストグラムを①~⑤のポイントに従って考察すると、①データの中心は60~70の階級、②データの散らばりの程度は普通、③分布のピークは1つで単峰性の分布、④データの分布はほぼ左右対称、⑤外れ値は存在しない、ということが分かります。
ヒストグラムの各柱の上辺の中心を直線で繋いだグラフを度数三角形(frequency polygon)と言い、各階級の上限と累積相対度数を直線で繋いだグラフを累積相対度数折れ線と言います。
棒グラフとヒストグラム
- 棒グラフ「独立した離散変数のデータの大小を比較する・因子変数の分布を要約する」
- ヒストグラム「連続変数のデータの分布を示す」
ただし、離散変数でも順序に意味がある場合(年齢・さいころ・質問紙調査による5点尺度など)は連続変数扱いすることがあり、離散変数の度数分布をヒストグラムで表すことがあります。