More than 3 years have passed since last update.

統計学的仮説検定

統計学

Last updated at 2020-09-01Posted at 2020-08-29

統計学的仮説検定

統計学的仮説検定とは、母集団分布の母数に関する仮説を標本から検証する統計学的方法です。

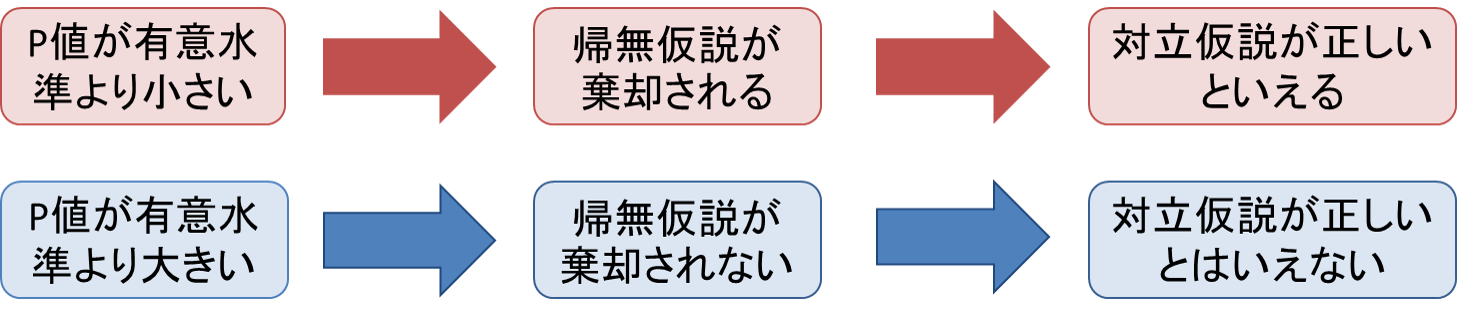
検定を行うために立てる仮説のことを「帰無仮説」と言い、帰無仮説に対立する仮説のことを「対立仮説」と言います。帰無仮説では、最終的に主張したい仮説を「否定する仮説」を設定し、背理法のように帰無仮説を否定することで主張を示します。

「薬の効果を有意的に主張できるか」を調べる薬の試験を例に取れば、帰無仮説は「薬の効果を主張できない」、対立仮説は「薬の効果を主張できる」に当たります。

※ 一般に帰無仮説をH0、対立仮説をH1で表します。

検定統計量とp値

サンプルデータから計算し、仮説検定で期待される値と比較するために使用されるランダム変数を検定統計量と言います。「帰無仮説が正しいと仮定した時に、統計量の実現値を超える統計量がたまたま得られる確率」であり、「帰無仮説の下で検定統計量がその値になる確率」をp値と言います。

p値が小さければ、標本から算出された統計量の実現値はたまたま得られたものではないと主張することができ、「p値 < 有意水準α（0.05が慣例）」である時、帰無仮説は妥当なものでないとして帰無仮説を棄却し、対立仮説を採択することができます。

画像引用：23-2. 検定で使う用語 | 統計学の時間 | 統計WEB

第Ⅰ種の過誤・第Ⅱ種の過誤

「帰無仮説が「正しい」にもかかわらず、誤って「正しくない」と判断をして棄却してしまう確率」を「有意水準α（危険率）」と言い、有意水準αはその帰無仮説を棄却する基準となります。

有意水準αは「第Ⅰ種の過誤」であるとも言います。また有意水準αと対するものとして、「帰無仮説が「正しくない」にもかかわらず、誤って「正しい」と判断をして棄却しない確率」という「検出力」があります。検出力は1-βで表せ、βは「第Ⅱ種の過誤」を犯す確率のことを指します。

第Ⅰ種の過誤▶︎「帰無仮説が真であるのに、帰無仮説を偽と棄却してしまう誤り」・危険率αである
第Ⅱ種の過誤▶︎「帰無仮説が偽であるのに、帰無仮説を真と棄却しない誤り」・βであり、検出力は1-βである

第Ⅰ種の過誤αと第Ⅱ種の過誤βは、「αを大きくするとβを小さくなる」というようなトレードオフの関係にあります。

棄却域・採択域

検定統計量を実際に計算した実現値が棄却域に入るか、採択域に入るかを判定します。
棄却域に入ることで、帰無仮説は棄却され、対立仮説は採択されます。

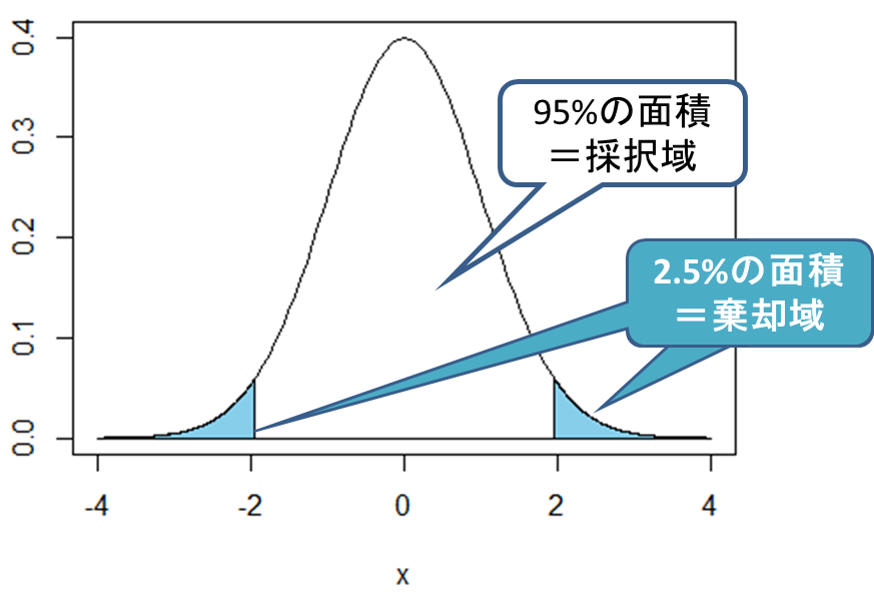
棄却域が片側にある場合を「片側検定」、棄却域が両端にある場合を「両側検定」と言います。
有意水準が5%である場合、片側検定なら右側/左側に5%の棄却域が設定され、両側検定なら両端に2.5%ずつ棄却域が設定されます。対立仮説について何も情報がない時は両側検定を選択し、事前に情報が得られており母数の変化自体を検定したい時は片側検定を選択します。

画像引用：23-5. 検定統計量と棄却域・採択域 | 統計学の時間 | 統計WEB

母平均の検定

仮説検定は以下の手順で実施します。

① 帰無仮説H0・対立仮説H1を立てる
② 検定統計量を決める（検定統計量は確率分布に従う）
③ 検定統計量を計算すると棄却域に入るため、帰無仮説は棄却され対立仮説は採択される

「検定統計量が棄却域に入り、帰無仮説が棄却された」とき、または「p値が有意水準αを下回った」とき統計的に有意であると言います。

母平均の検定は、1つのデータ（1標本・1群）を用いて実施し、「母分散既知」と「母分散未知」の2つの場合があります。母分散既知の場合はZ検定、母分散未知の場合はt検定となります。

母分散既知の1標本

母分散既知の1標本で母平均の検定を行う際は、検定統計量Zが標準正規分布に従う（Z検定）ことを利用して検定を行います。検定統計量Zは以下のように表せます。

Z=\frac{\bar{x}-\mu}{\frac{σ}{\sqrt{n}}}

母分散未知の1標本

母分散未知の1標本で母平均の検定を行う際は、検定統計量tが自由度n-1のt分布に従う（t検定）ことを利用して検定を行います。検定統計量tは不偏分散s^2の値を用いて以下のように表せます。

t=\frac{\bar{x}-\mu}{\frac{s}{\sqrt{n}}}

母平均の差の検定

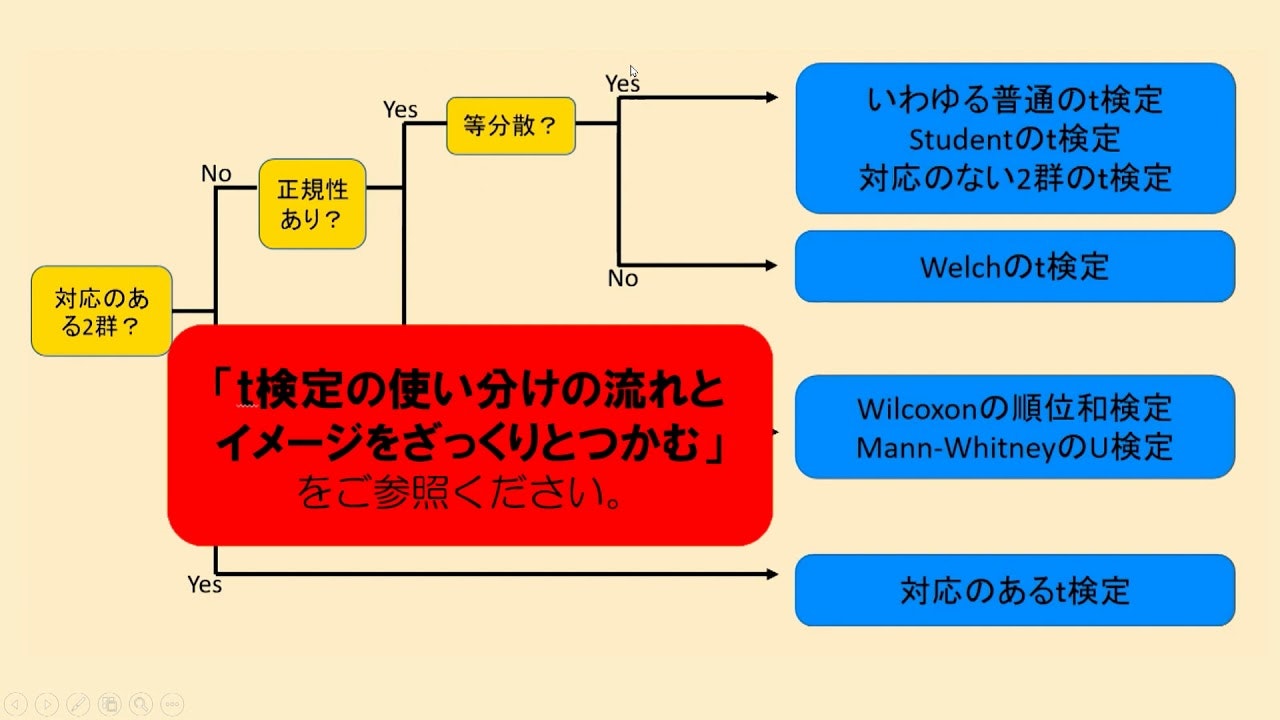
母平均の差の検定は、2つのデータ（2標本・2群）を用いて実施し、「対応のある2標本」と「対応のない2標本」の2つの場合があります。対応のある2標本・対応のない2標本のどちらの場合もt検定となりますが、対応のある2標本は実質的に母分散未知の1標本と同じ形になります。

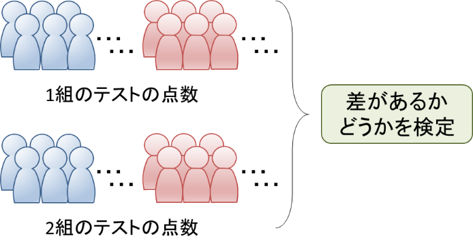
母平均の差の検定では、2つの独立した母集団から標本を抽出した際に「平均に差があるかどうか」を検定します。「対応のある2標本」とは「投薬前後で得られた同一な薬の被験者の2つのグループ」というように、同一の対象から抽出された2つの標本のことであり、2つの標本の母集団は同じであるため、その2つの母平均の差は0になります。「対応のない2標本」とは「1組と2組のテストの点数の結果」というように、異なる対象から抽出された2つの標本です。

画像引用：24-3. 2標本t検定とは | 統計学の時間 | 統計WEB

対応のある2標本

対応のある2標本で母平均の差の検定を行う際は、検定統計量tが自由度n-1のt分布に従う（t検定）ことを利用して検定を行います。検定統計量tは不偏分散s^2の値、2つの標本平均x1,x2、母平均の差（μ1-μ2）が0であることを用いて以下のように表せます。

t=\frac{\bar{x_1}-\bar{x_2}}{\frac{s}{\sqrt{n}}}

対応のない2標本

対応のない2標本では2つの母分散が等しいという前提（等分散性の仮定）で、2つの標本をまとめた「プールした分散s^2」というものを自由度n1-1,n2-1に注意して以下のように設定します。

s^2=\frac{(n_1-1)・s_1+(n_2-1)・s_2}{n_1+n_2-2}

検定統計量tが自由度「n1+n2-2」のt分布に従う（t検定）ことを利用して検定を行います。検定統計量tはプールした分散s^2の値、2つの標本平均x1,x2、母平均の差（μ1-μ2）が0であることを用いて以下のように表せます。

t=\frac{\bar{x_1}-\bar{x_2}}{\sqrt{\frac{s^2}{n_1}+\frac{s^2}{n_2}}}　（s^2はプールした分散）

等分散であり、対応のない2標本のt検定を「スチューデントのt検定」と言います。

ウェルチのt検定

対応のない2標本の母平均の差の検定では、2つの母分散が等しいという仮定（等分散性の仮定）のもと検定を進めていきますが、2つの標本の母分散が等しいと仮定できない場合、「ウェルチのt検定」という手法を用います。検定統計量tは以下のように表せ、その統計量はt分布に従います。

t=\frac{\bar{x}_1-\bar{x}_2}{\sqrt{\frac{s^2_1}{n_1}+\frac{s^2_2}{n_2}}}

画像引用：EZRでｔ検定②：等分散ではないｔ検定（ウェルチのｔ検定）

母比率の検定

母比率の検定を行う際は、サンプルサイズnが十分に大きいとき検定統計量Zが標準正規分布に従う（Z検定）ことを利用して検定を行います。検定統計量Zは標本比率p^、母比率pの値を用いて以下のように表せます。

Z=\frac{\hat{p}-p}{\sqrt{\frac{p(1-p)}{n}}}

二項分布・ポアソン分布の検定

期待値E[X]=np,分散V[X]=np(1-p)である二項分布、期待値E[X]=λ,分散V[X]=λであるポアソン分布では、それぞれサンプルサイズnが十分に大きいとき検定統計量Zが標準正規分布に従う（Z検定）ことを利用して検定を行います。

Z=\frac{x-np}{\sqrt{np(1-p)}}　（Zは二項分布の検定統計量）

Z=\frac{x-nλ}{\sqrt{nλ}}　（Zはポアソン分布の検定統計量）

母比率の差の検定

母比率の差の検定では、2つの標本比率をまとめた「プールした標本比率p^」というものを以下のように設定します。

\hat{p}=\frac{n_1\hat{p}_1+n_2\hat{p}_2}{n_1+n_2}

サンプルサイズnが十分に大きいとき検定統計量Zが標準正規分布に従う（Z検定）ことを利用して検定を行います。検定統計量Zはプールした標本比率p^、母比率pの値を用いて以下のように表せます。

Z=\frac{\hat{p}_1-\hat{p}_2}{\sqrt{\hat{p}(1-\hat{p})\Bigl(\frac{1}{n_1}+\frac{1}{n_2}\Bigr)}}　（\hat{p}はプールした標本比率）

母分散の検定

母集団が母分散σ^2の正規分布N(μ,σ^2)に従う時、抽出された標本のサンプルサイズをn、不偏分散s^2をとすると、以下で示される検定統計量χ^2が自由度n-1のカイ2乗分布に従うことを利用して検定を行います。

χ^2=\frac{(n-1)・s^2}{σ^2}　（s^2は不偏分散）

等分散の検定

2つの標本の不偏分散s^2の比の検定を等分散の検定と言います。
検定統計量Fを以下のように設定すると、検定統計量Fは自由度(n1-1,n2-1)のF分布に従います。
Fを算出する際は、F>0となるように大きな値の不偏分散を分子にします。

F=\frac{s_1^2}{s_2^2}

カイ2乗検定

帰無仮説が正しいとき、検定統計量χ^2が漸近的にカイ2乗分布に従うような統計的検定法をカイ2乗検定と言います。観測度数をO、期待度数をE（=n×理論比率p）とすると、検定統計量χ^2は以下のように表せます。

χ^2=\sum_{i=1}^{n}\frac{(O-E)^2}{E}

カイ2乗検定にはクロス集計表を用いた「適合度検定」と「独立性検定」の2種類があります。

適合度検定

「観測度数がある特定の分布に一致するかどうか」を検定する方法を適合度検定と言います。
▶︎帰無仮説の例「調査した血液型分布は日本人の血液型分布と一致する」

適合度検定の場合、自由度「列数-1」のカイ2乗分布に従います。

画像引用：適合度検定をカイ二乗検定で行う例題と手順 | AVILEN AI Trend

独立性検定

2つ以上の分類基準を持つクロス集計表において、「分類基準間に関連があるかどうか」を検定する方法を独立性検定と言います。
▶︎帰無仮説の例「性別と血液型は独立である（関連がない）」

独立性検定の場合、自由度「（列数-1）×（行数-1）」のカイ2乗分布に従います。

イェーツの補正（連続性の補正）

2行×2列のクロス集計表において、本体は離散値である確率を連続型確率分布であるカイ2乗分布に近似させることで、危険度αの値が大きくなる（p値が小さくなる）ということが起きるため、0.5を加減して適合度検定統計量χ^2に修正を加えることを「イェーツの補正（連続性の補正）」と言います。

χ^2=\sum_{i=1}^{n}\frac{(｜O-E｜-0.5)^2}{E}

参考文献

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up