はじめに
年末の振り返りの代わりに、11月に某学会にsubmitした論文を宣伝します。これは僕が今の所属になって初めての論文です。
元論文は
Liyuan Xu, Yutian Chen, Siddarth Srinivasan, Nando de Freitas, Arnaud Doucet, Arthur Gretton, "Learning Deep Features in Instrumental Variable Regression".
[PDF]
この論文は因果推論の有力な手法である操作変数法というものをディープラーニングで行う手法を提案したものです。今回@tkanayama_さんがブログで使っていたポケモンの例を使って、自分の手法を説明します。
操作変数法について
まず、簡単な例を用いて操作変数法とは何なのか説明します。
問題設定
@tkanayama_さんのブログ記事「ポケモンを題材に因果推論を実践してみる」と同じ問題を考えます。
今は昔、モンスターボールしか存在せず、スーパーボールが世の中で出回り始めたばかりの頃、オーキド博士が「スーパーボールは本当にモンスターボールより捕まえやすいのか?」という仮説を検証しようとしています。
そこでオーキド博士は世界中のトレーナーたちからデータを収集し、下記のような100件のデータを収集することができました。
|データID |使ったボール |捕まえたポケモン |ポケモンを捕まえるのに使ったボールの個数|
|---|---|---|---|
|1 |モンスターボール | コラッタ| 3個|
|2 |スーパーボール | イワーク| 2個|
|・・・ |・・・ |・・・ |・・・|
|100 |スーパーボール| フシギダネ| 4個|
オーキド博士はさっそくこれらのデータを用いて、モンスターボール・スーパーボールそれぞれに対し、捕まえるのに使ったボールの個数の平均値を算出しました。
| ボール | ポケモンを捕まえるのに使ったボールの個数の平均値 |
|---|---|
| モンスターボール | 5.22個 |
| スーパーボール | 6.74個 |
予想に反して、スーパーボールのほうがモンスターボールよりも個数が多くなってしまいました。この結果だけ見ると、「スーパーボールはモンスターボールよりポケモンを捕まえにくい」と言えそうです。
データだけを見ると**「スーパーボールはモンスターボールよりポケモンを捕まえにくい」**という直感に反する結果が生まれてしまいます。ブログ記事ではこの後オーキド博士は
「捕まえやすそうなポケモンにはモンスターボールを使い、捕まえにくそうなポケモンにはスーパーボールを使っている」
という事実を見つけます。これは「ポケモンの捕まえやすさ」が「どちらのボールを使うか」ということと「必要だったボールの個数」の両方に影響する交絡因子となっているということに他なりません。このような交絡因子があるとただ単に平均を比べたときに結論がバイアスしてしまいます。今回の場合、スーパーボールのほうが必要なボールの個数が多くなったのは、性能の差ではなく、捕まえにくいポケモンを捕まえようとしていたからという事になっていしまいます。もともとのブログ記事ではこれを解消するために、交絡因子となっている「ポケモンの捕まえにくさ」のデータを取得し分析する方法を紹介しています。
操作変数法
しかし、交絡因子のデータを収集するアプローチはいつでも適用可能であるとは限りません。「ポケモンの捕まえやすさ」以外の交絡因子(例えばポケモンの残り体力や状態異常など)があるかもしれませんし、ともすると**「ポケモンの捕まえやすさ」を測定する方法がないかもしれません。そのような場合に使える方法が操作変数法**です。
操作変数法では以下の因果モデルを仮定します。
Y = f_\mathrm{struct}(X) + U, \quad \mathbb{E}[U] = 0, \quad \mathbb{E}[U|X] \neq 0
ここで$Y$がアウトカム(この場合、必要なボールの数)、$X$が処置(この場合使うボールの種類)、そして$U$が交絡因子由来のノイズです。ここで$f_\mathrm{struct}$は因果効果を表し、これを推定することが目的です。(より専門的には平均処置効果 (Average Treatment Effect)とよびます。)この問題の例では「平均的なポケモン」を捕まえるのに必要なボールの個数が$f_\mathrm{struct}$となります。
ここで$\mathbb{E}[U|X] \neq 0$が交絡因子の存在を表し、このために$\mathbb{E}[Y|X] \neq f_\mathrm{struct}(X)$となってしまっています。 このようなときに、以下のような操作変数$Z$を考えます。
- 処置$X$と操作変数$Z$は互いに独立ではない
- $\mathbb{E}[U|Z] = 0$である
今回の場合**「トレーナーがスーパーボールを持っていたかどうか」が操作変数として使えます。つまりトレーナーがモンスターボールを使ったときに、「スーパーボールを温存したのか」それとも「モンスターボールしかそもそも持っていなかったのか」**というデータを収集することで因果効果を推定できます。
実際、スーパーボールを持っていないとそれを使うことはできないので、条件1「処置$X$と操作変数$Z$は互いに独立ではない」はクリアします。また、スーパーボールを持っているかどうかは捕まえようとするポケモンと関係がない 1 ので条件2「$\mathbb{E}[U|Z] = 0$である」も満たされます。
このような操作変数$Z$を用いると、因果モデルの式の両辺を操作変数を条件づけて期待値をとることにより、
\mathbb{E}[Y|Z] = \mathbb{E}[f_\mathrm{struct}(X)|Z]
となります。今回の場合は処置$X$と操作変数$Z$がどちらも二値の値を取るので上の方程式をそのまま解くことができます。(より一般的な操作変数法は後述します。)今、データを取った結果、以下のようになったとします。2
| モンスターボールを使った | スーパーボールを使った | |
|---|---|---|
| スーパーボールを持っていない | 平均:7.58個(件数:10件) | 平均:NA (件数:0件) |
| スーパーボールを持っていた | 平均:4.63個(件数:40件) | 平均:6.74個(件数:50件) |
| 合計 | 平均:5.22個(件数:50件) | 平均:6.74個(件数:50件) |
いま、$\theta_1 = f_\mathrm{struct}(X=\text{スーパーボール})$、$\theta_0 = f_\mathrm{struct}(X=\text{モンスターボール})$ とします。このとき、各件数から、以下が成り立ちます。
\mathbb{E}[f_\mathrm{struct}(X)|Z=\text{スーパーボールを持っていた}] = \frac{40}{40+50} \theta_0 + \frac{50}{40+50} \theta_1\\
\mathbb{E}[f_\mathrm{struct}(X)|Z=\text{スーパーボールを持っていない}] = \theta_0
また、操作変数について平均を取ると
\mathbb{E}[Y|Z=\text{スーパーボールを持っていた}] = \frac{40}{40+50} 4.63 + \frac{50}{40+50} 6.74 = 5.80\\
\mathbb{E}[Y|Z=\text{スーパーボールを持っていない}] = 7.58
これを元に、方程式$\mathbb{E}[Y|Z] = \mathbb{E}[f_\mathrm{struct}(X)|Z]$を解くと
\theta_0 = 7.58 \quad \theta_1=4.38
となり、スーパーボールのほうが平均的には捕まえるのに必要なボールが少なくなります。このようにして、操作変数をもちいて交絡因子によるバイアスを修正するのが操作変数法です。
一般的な操作変数法
ここからは、より一般的な操作変数法と、論文の貢献をまとめます。
二段階最小二乗法
より一般的に、二値ではない操作変数$Z$と処置$X$において因果効果$f_\mathrm{struct}$を求めるときには、上のように方程式$\mathbb{E}[Y|Z] = \mathbb{E}[f_\mathrm{struct}(X)|Z]$を解くことができません。そのため、以下のような損失関数の最小値として因果効果 $ \hat{f}_\mathrm{struct} = \arg\min \mathcal{L}(f)$ を推定します。
$$\mathcal{L}(f) = \mathbb{E}[(Y - \mathbb{E}[f(X)|Z])^2] + \Omega(f)$$
ここで$\Omega(f)$は適当な正規化項です。この最適化問題を解くために以下のような**二段階最小二乗法(Two-stage Least Square)**を用いることが提案されていました。いま、適当な基底関数$\psi(x)$をもちいて$f_\mathrm{struct}(x) = u^\top \psi(x)$であるとします。ここで$u$がパラメータで学習するものです。すると、損失関数は
\mathcal{L}(u) = \mathbb{E}[(Y - u^\top\mathbb{E}[\psi(X)|Z])^2] + \lambda \|u\|^2
と書き換えられます。ただし、$\Omega(f) = \lambda |u|^2$であるとしてます。ここで、この条件付き期待値$\mathbb{E}[\psi(X)|Z])^2]$が$\mathbb{E}[\psi(X)|Z])^2] = V\phi(Z)$と書けるとします。ただし、$\phi(Z)$は別の基底関数で$V$はパラメータで学習するものです。ここで最適な$V$は
\mathcal{L}_{\mathrm{stage1}}(V) = \mathbb{E}[(\psi(X) - V\phi(Z))^2] + \eta \|V\|^2
を最適化することで得られます。まとめると、
-
以下を最小化して$\hat{V} = \arg \min \mathcal{L}_{\mathrm{stage1}}(V)$を求める。
\mathcal{L}_{\mathrm{stage1}}(V) = \mathbb{E}[|\psi(X) - V\phi(Z)|^2] + \eta |V|^2
```
-
求められた$\hat{V}$を用いて最適な $\hat{u}= \arg \min \mathcal{L}_{\mathrm{stage2}}(u)$ を求める
\mathcal{L}_{\mathrm{stage2}}(u) = \mathbb{E}[(Y - u^\top \hat{V} \phi(Z))^2] + \lambda |u|^2
```
- 求められた$\hat{u}$ を用いて$\hat{f}_\mathrm{struct}(X) = \hat{u}^\top \psi(X)$と計算する。
ここで、手順1,2での最小化は通常の線形回帰と同様の方法で解析解を求めることができます。
論文の貢献
上の二段階最小二乗法は解析解がすぐに求まる一方、基底関数$\psi, \phi$を事前に決めなくてはいけません。そのため、論文では**基底関数$\psi,\phi$をDeep Learningで表して学習する方法を提案しています。**その結果、様々なタスクにおいて他の操作変数法の精度を超えるスコアを出しました。 以下が一つの実験結果のグラフです。
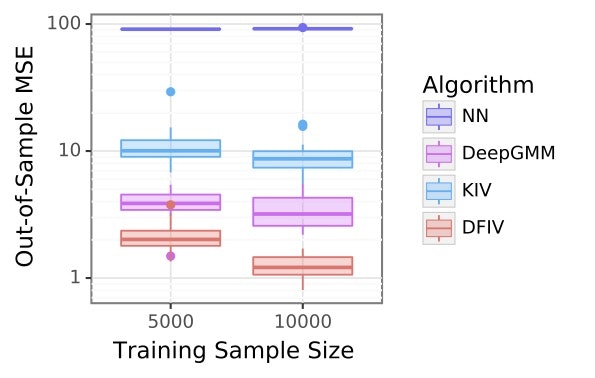
上のグラフは各手法の精度をプロットしたもので縦軸が誤差です。DFIVが提案手法でこれが一番精度が良いことがわかります。詳しい提案手法の詳細や実験の設定は元論文を参照してください。
実装はGithubにあります。