はじめに
Machine Learning Summer School 2020 でなされた、機械学習の公平性についてのレクチャー(by Prof. Moritz Hardt)が面白かったので勉強用にノートを残します。もとのレクチャーの動画はYoutubeに公開されています。この記事内で引用しているスライドは特に指定しない限り、レクチャーのスライドから引用しています。
Link集
[動画Part1][動画Part2][スライド]
TL;DR
- **「センシティブ情報はデータに含まれないから差別していない」**は通用しない
- センシティブ情報を保護するために満たすべき基準が提案されている
- しかし、これは差別的扱いを完全には防げない
- 特に、データのSelection Biasがあると、差別的な扱いにつながってしまう
-
因果関係を考慮した基準ならSelection Biasがあっても差別的な扱いをある程度は防げる
- しかし、正しい因果関係を見つけられるかどうかという新たな問題を生む
- これが本当に差別的扱いを完全に防いでいるかも議論が必要
そもそも「公平性」とは?何故必要?
BlackLivesMatter運動など差別に対する関心が近年高まっています。この傾向はアカデミックな機械学習の分野も無関係ではなく、モザイク除去の研究が人種差別の議論に発展するであったり、機械学習のトップ会議が論文に「社会へのインパクト」を明記することを義務化したり、社会の要請に答えて技術を発展させようという姿勢が明確になってきました。この流れを受けて、機械学習における「公平性」が近年注目されています。この記事ではその流れを簡単にまとめています。
適応ドメインとセンシティブ情報
「差別」と一口にいっても、いろいろな形があります。この記事では「意思決定における差別」を扱います。特にその人の人生に大きな影響を与える場面において、その人のある属性によって不当に判断される形での差別を考え、これを防ぐための機械学習技術を考えます。どういったものが「大きな影響を与える場面」かは、この記事では議論しませんが、例えばアメリカの法律では「入試」や「求職」などの場面で不当な扱いを行うことを禁止していますし、マーケティングなどでもあまり望ましいものではないでしょう。
またどの属性に基づいて判断することが差別に当たるか、(これをセンシティブ情報と言います)ということも場面や社会情勢などによって変わり得ます。「性別」や「人種」などによる差別は法律によって明確に禁止されていますし、また道徳的な観点から「障碍のあるなし」を雇用のときに考慮することは(法律によって禁止されていなかったとしても)問題でしょう。何をセンシティブ情報とするかも、ここでは議論しないことにします。
「無知による無差別」の失敗
このような「公平性」に関する議論でよくある間違いは、センシティブ情報をデータに含まなければ良いというものです。これをレクチャーでは「無知による無差別」(原文: fairness through unawareness)と呼び、これでは差別的な扱いを防ぐことができないと主張しています。これの具体例として、以下のAmazonの当日配達のサービスを提供している区域の例が出されています。

上の図はアメリカの各地域で、Amazonが当日配達のサービスを実施している区画なのですが、これが白人の住む割合の多い地域とほぼほぼ重なっていると指摘しています。もちろんAmazonは人種のデータを得ていないはずですが、「Amazonの売上の多い地域」を予測しようとした結果、「裕福な人が多く住んでいる地域」、ひいては「白人の多く住んでいる地域」にサービスを提供してしまっているのです。このような効果はRedliningとも呼ばれ、いろいろな場面で観測されます。そのため、差別を防ぐためには、センシティブ情報を取得しないのではなくむしろ、センシティブ情報を取得した上で、それによって予測が変わらないようなモデルを作る必要があります。
モデルの統計情報による公平性の基準
以上の議論により、公平性のためにはセンシティブ情報を取得した上で、その情報によって予測が変わらないモデルを学習する必要があることがわかりました。しかし一口で「予測が変わらない」といっても様々な切り口があります。ここでは、もっとも単純な、モデルの予測の統計情報をもとにした公平性の基準とそれを達成するための学習方法を紹介します。
設定としては以下の、二値分類のケースを考えます。予測に用いるFeatureを$X$, 正解ラベルを$Y\in \{0,1\}$, センシティブ情報を$A$とします。このとき、目的は$Y$を$X$から予測することで、これはあるスコア$R(X)$と閾値$t$をデータから学習し、スコア$R$が$t$より大きいかどうかにより予測値$D = \mathbb{1}(R(X) > t)$を出力します。
具体例としてクレジットカードの審査を考えましょう。このとき、$X$はその人の年収や資産などの情報で$Y$はその人にお金を貸すべきか(≒ちゃんとお金を返せるかどうか)であり、資産情報からこれを予測したいとします。このとき、我々は**信用スコア$R(X)$をデータから学習し、それがある閾値$t$を超えるかどうかで$Y$を予測します。このときに、予測が性別や職業などのセンシティブ情報$A$によって「変わらない」ことを要請するのがゴールです。このとき、以下のようにいくつかの「公平性」**の定義があります。
Demographic parity
もっとも単純な公平性の定義は、あるセンシティブ情報$a$と$b$において
$$P(D = 1 | A = a) = P(D = 1 | A = b)$$
というものです。もっと言うと、予測とセンシティブ情報が独立であることを要請するのがこの制約です。これを達成する方法は色々考えられていますが、代表的なものは表現学習によるもので、**$X$の情報を保持しながら、$A$と無相関な表現$Z$を学習し、それをもとにスコア$R(Z)$**を学習するというものです。代表的な論文はLearning Fair Representations (Zemel et al. 2013)です。
これは、「予測がセンシティブ情報によって変わらない」をそのまま数式に落とした形になっており、とても直感的です。しかし、これではマジョリティーなセンシティブ情報を持つ人は正しく判断し、マイノリティーなセンシティブ情報を持つ人にはランダムに判断するモデルもこの制約を満たしてしまいます。これは信用スコアの例で行くと、サラリーマンからの申請はちゃんとまじめに審査し、Youtuberなどからの申請はいい加減な審査をするということで、サラリーマンの申請が圧倒的に多い場合だと、全体としての精度は高いものの、これは不公平になってしまいます。
Error rate parity
前のDemographic parityではセンシティブ情報によって精度が変わることを許容してしまっていました。これを一致させるべきだ、という基準がError rate parityで、数式で書くと
$$
P(D = 1 | Y = 0, A = a) = P(D = 1 |Y = 0, A = b)\\
P(D = 0 | Y = 1, A = a) = P(D = 0 |Y = 1, A = b)
$$
というものです。一般的には、予測$D$とセンシティブ情報$A$がラベル$Y$の下で条件付き独立であるというものです。代表的な論文はEquality of Opportunity in Supervised Learning (Hardt et al. 2016)で、この中では学習されたの任意のモデルをこの基準を満たすように変換する方法が議論されています。直感的には、この基準は以下のような図で理解されます。
上の図のように、各グループの達成可能なROC曲線を書いたときに、この基準は最終的なスコアのROC曲線がすべてのグループのROC曲線よりも下側に来ることを要請します。そのため、グループによっては性能が激しく劣化する可能性があるのが欠点です。
この弱点としてはあるモデルがこれを満たしているかどうか判定するのが難しい点です。信用スコアの例で言うと、この基準は**「クレジットカードの審査に通った人$(D=1)$の中で、債務不履行を起こした人$(Y=0)$の割合」と、「クレジットカードの審査に落ちた人$(D=0)$のなかで、ちゃんとお金を返した人$(Y=1)$の割合」**が、サラリーマンとYoutuberで同じであることを要請するのですが、後者は(そもそも審査に落ちるとお金を借りられないので)データを集められないし、前者はデータを集めること事態は可能なものの、その時点では審査は終わってしまっているという問題があります。
Group calibration
二値分類において、Calibrationという概念があります。これは、スコア$R$が確率のように振る舞うというもので、数式で書くと
$$P(Y = 1 | R = r) = r$$
というものです。このCalibrationがすべてのグループにおいて満たされていることを要請するのがGroup calibrationで数式は
$$P(Y = 1 | R = r, A = a) = r$$
となります。注意としてはこれは**$R=0.8$と予測された人の集合で$Y=1$となる確率の"平均"が0.8となるということを意味しており、$R=0.8$と予測された"その人"が$Y=1$となる確率が0.8となることを意味しているわけではない**ということです。上の数式は
$$P(Y = 1 | R = r, A = a) = P(Y = 1 | R = r, A = b)$$
を意味しているので、モデルの予測のもと、ラベル$Y$とセンシティブ情報$A$が独立であることを意味します。直感的には「どのグループにおいても、正確な確率を予測できている」ことを要請するのがGroup calibrationの意味です。
このGroup calibrationは、実は特に特別な制約を与えなくても、普通の機械学習によって達成されることが知られています。

上のグラフは年収がある値を超えるかどうかを予測する問題で、特別な制約を与えずに学習したモデルの予測値を性別ごとにプロットしたものです。横軸は予測の確率(の十倍)、縦軸は実際の確率で、これを見るとたしかにGroup Calibrationが成り立っていることがわかります。元論文はThe Implicit Fairness Criterion of Unconstrained Learning (Liu et al. 2019)で、これに対する理論的な評価も与えています。
不可能性定理
これまで以下の3つの基準を見てきました。
- Demographic parity: 予測$D$とセンシティブ情報$A$が独立
- Error rate parity:: 予測$D$とセンシティブ情報$A$がラベル$Y$のもとで条件付き独立
- Group calibration: ラベル$Y$とセンシティブ情報$A$が予測スコア$R$のもとで条件付き独立
それぞれの基準には一長一短あるのですが、このうちの2つを同時に達成することは不可能であることが知られています。そのため、状況によってどの基準を使うかを決めることが必要です。また、あるセンシティブ情報について公平性を担保しようとすると、別のセンシティブ情報をもとに差別してしまうこともあることが知られています。
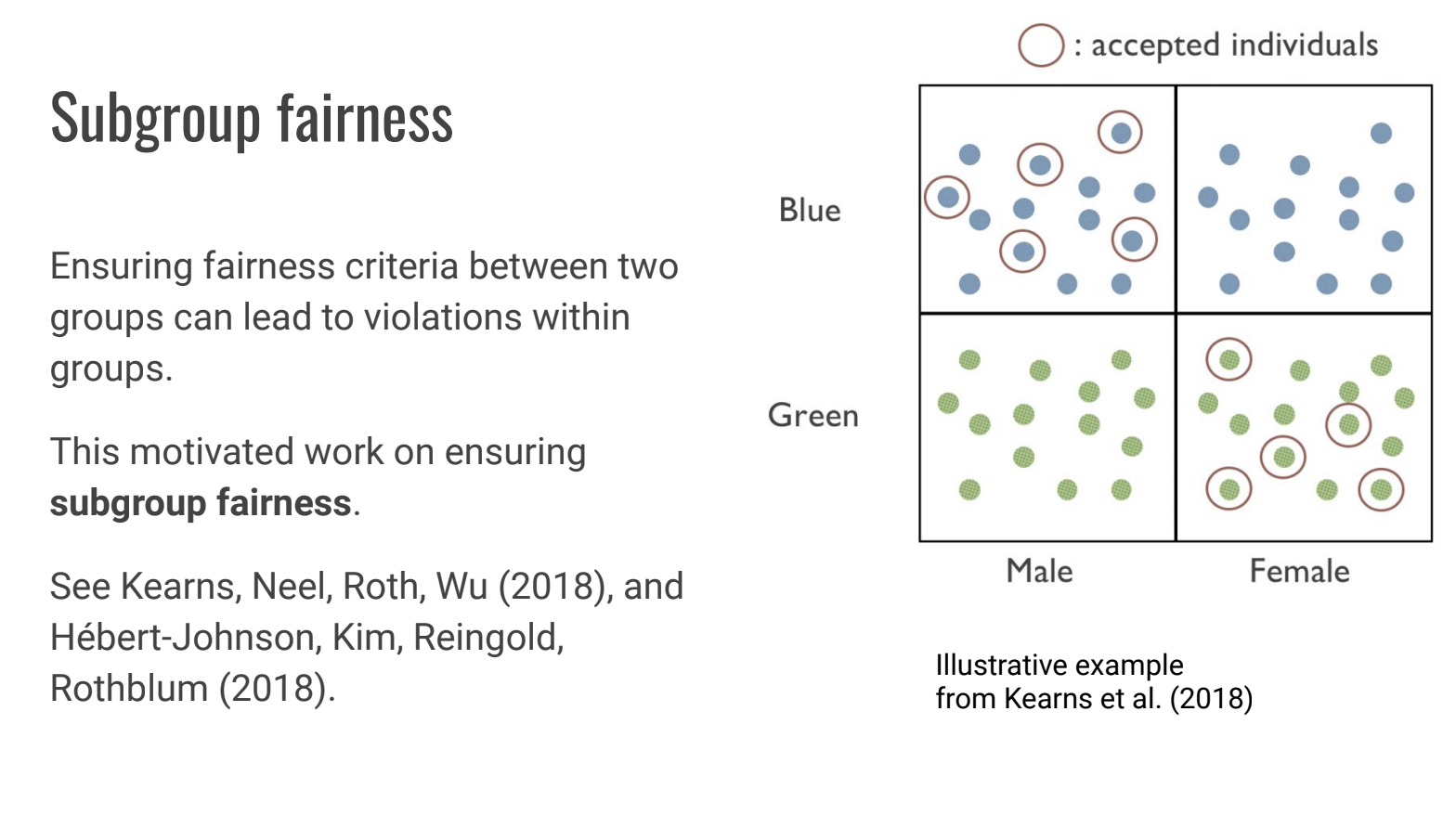
因果推論に基づく公平性の基準
これまでの議論はモデルの予測$D$とラベル$Y$、そしてセンシティブ情報$A$の統計情報のみで公平性を議論してきました。しかし、これから見ていく通り、データのSelection Bias(選択バイアス)があるとき、これでは不公平な振る舞いを防げません。そのため、因果関係を考慮した公平性の基準も考えられています。
COMPASに見る統計情報による公平性の定義の限界
COMPASとは、犯罪者たちの再犯可能性を予測するために導入されたシステムで、これが黒人に対してより高いスコアをつけている(再犯可能性が高いと予測している)ということが2016年に問題になりました。
上のスライドはそれを象徴したもので、左の黒人の方が再犯可能性が高いと判定されたのですが、右の白人の方が実際には再犯を犯し、三度も逮捕されたそうです。実際にこの問題を告発したProPublicaという新聞社は「再犯を犯さなかった人のなかでCOMPASによって高リスクと判定された割合は黒人のほうが圧倒的に高い」という事実を見つけ、「黒人の方がより厳しい基準を課せられているのではないか」と主張しました。再犯を犯さない($Y=0$)人の中で、高リスクという予測($D=1$)を受けた人の割合を見ているので、これは**「Error rate parity」が成り立っていない**という主張をしていることになります。
一方、システムの作成者であるEquivalent社側は、これに対し、「COMPASはきちんとその人の再犯率を予測できている。もともと黒人の再犯率というのは白人より高いので、基準が厳し目になり、Error rate parityが成り立たないのは仕方がないことだ。」という反論をしました。これはまさに「Group calibrationが成り立っているので公平だ」と主張していることにほかなりません。そのため、この議論はError rate parityを選ぶか、Group calibrationを選ぶかという論点で見られがちです。
しかしレクチャーではError rate parityもGroup calibrationも、この件で不公平な振る舞いを防ぐことはできないと結論づけています。それを以下の例によって説明します。

いま青とオレンジの2つのグループがあるとしましょう。仮にその人が再犯する確率が分かっていたとします。(人の下の数字はその人が再犯確率を表しています。)仮にこの確率が0.5以上の人を勾留(Detain)し、それ未満の人を保釈するとしましょう。このとき、スコアは正しい確率なので、Group calibrationは成り立っているものの、オレンジのグループのほうがより多く勾留されていて(Detantation rateが高く)、また再犯を犯さなかった人のうち勾留される人の割合もオレンジのほうが高いです(False positive rateがオレンジのほうが高い)。つまり、現状のルールではGroup calibrationは成り立っているものの、Demographic parity や Error rate parityが成り立っていない状況を反映しています。
しかし、この状況は警察がオレンジの再犯リスクの低い人達を追加で逮捕し、釈放することで解消することができます。

これにより、全体としてオレンジの勾留率が下がるためDemographic parityがある程度満たされ、再犯しない人を正しく保釈できているのでError rate parityもある程度満たす事ができます。しかしこれではオレンジの人を多く逮捕するという意味で不公平でしょう。
さらにGroup calibrationにも以下のような問題があります。

いま、再犯を犯す正しい確率が上であるとわかっているとしましょう。このとき確率0.5以上を勾留するとすると、5人勾留されることになります。**これは正しい確率を用いて分類しているのでGroup calibrationが成り立っています。**しかし勾留される五人と低リスクの5人を集めて、全てスコア0.4を与えるとするとと、これも「スコア0.4を得た人たちの中で再犯を犯す確率の平均は0.4」を満たしているのでGroup calibrationが成り立っています。こうすることにより、Group calibrationを満たしたまま、青グループの人をだれも勾留しないという事が可能になるのです。
そのため、この状況ではDemographic parity, Error rate parity, Group calibrationのいずれもオレンジに対する差別的な結果を防ぐことができないということがわかります。
因果推論に基づく公平性
前の例では統計情報に基づいた基準で不公平な振る舞いを防ぐことができませんでした。これは警察が誰を逮捕するかによってデータが変わってしまうからです。これによって、特定のグループを多く逮捕することにより公平性を担保するという、意図していない選択が可能になってしまうのです。このように、**データの集め方でデータが歪んでしまうことSelection biasと呼びます。**これに対応するためにデータの集め方を含めて、モデルを学習するのが因果推論です。
これを説明するために、以下のような例を見てみましょう。1973年にUC Berkleyの入試において男女差別があったのではということが問題になりました。人気な6つの学部において、男性の合格率が44%だったのに対し、女性の合格率は33%だったそうです。しかしそれらの学部ごとの合格率をみると状況は変わります。
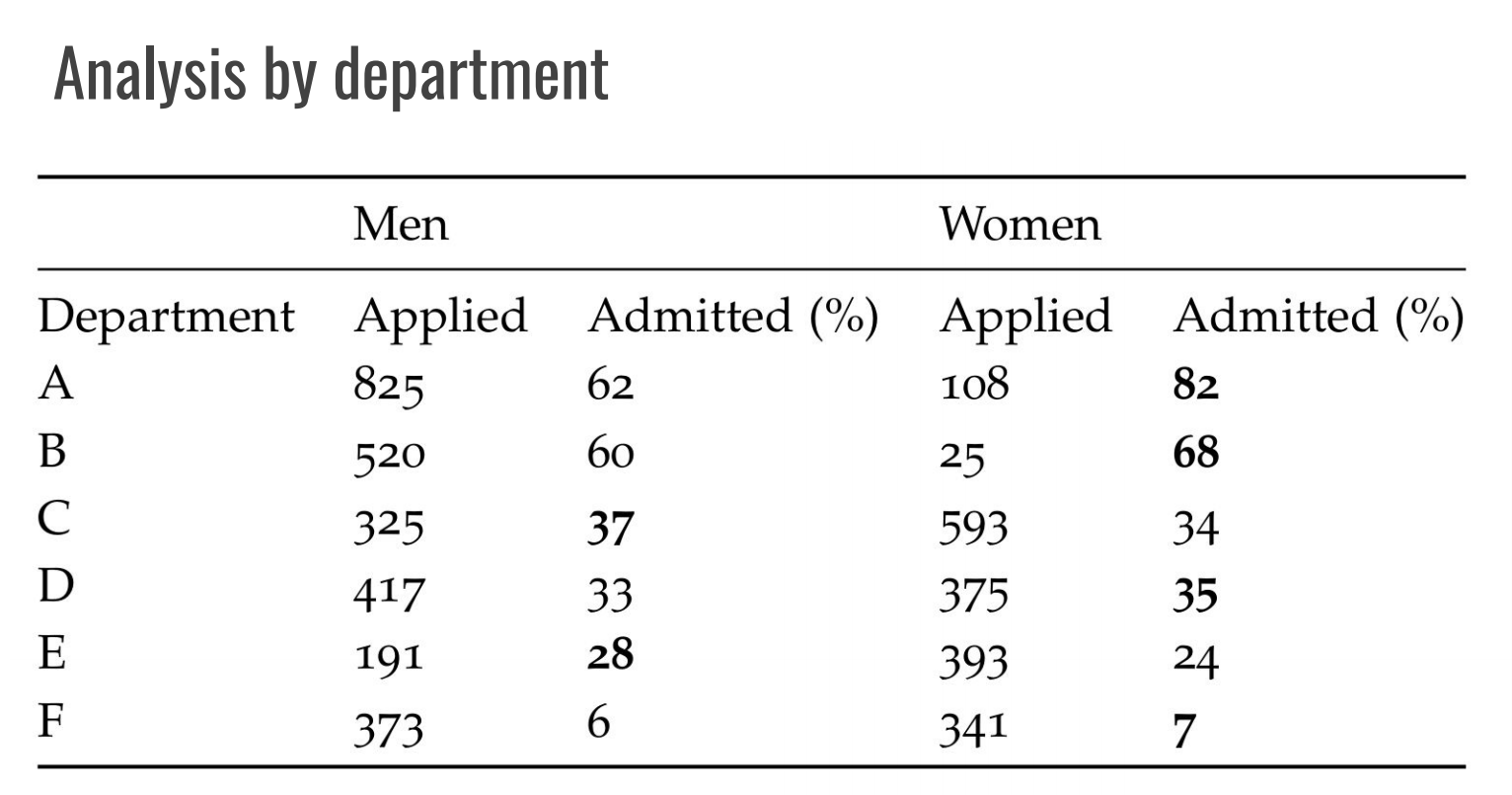
上の表は男女の合格率を学部ごとに集計したもので、これを見るとどの学部も男性を有意に差別していない事がわかります。それどころか、学部Aに関しては女性の方が遥かに合格率が高かったのです。それでもほとんどの女性が合格率の低い学部を主に志望しているのに対し、男性は過半数が合格率の高い学部Aを志望したことで全体としての合格率に差が出たというのが実情でした。
上図において各ノードは特徴を示し、矢印は因果関係を示します。ここでGender→Admissionの矢印の存在はその人の性別により合格かどうかが決まったということで差別に当たりますが、「性別が応募する学部に影響を与えそれが合否に影響を与えている」 (つまり、 Gender→Department→Admissionのパスがある)場合は、合否に性別が影響を与えていたとしても差別には当たらないと言えます。ここで前者をDirect effect、後者をIndirect effectと呼びます。それぞれの効果の大きさは以下によって計算されます。
$$TE_{a,b}(Y) = \mathbb{E}[Y | A=a] - \mathbb{E}[Y | A=b] = DE_{a,b}(Y) + IE_{a,b}(Y) \\
DE_{a,b}(Y) = \mathbb{E}[Y | A=a] - \int \mathbb{E}[Y | A=b, Z=z] \mathrm{d}P(Z=z|A=a) \\
IE_{a,b}(Y) = \int \mathbb{E}[Y | A=b, Z=z] \mathrm{d}P(Z=z|A=a) - \mathbb{E}[Y | A=b]
$$
ここで、$TE_{a,b}(Y)$とはtotall effectの意味で、センシティブ情報がそれぞれ$a,b$のときのラベル$Y$の期待値の差で、これはDirect effect $DE_{a,b}(Y)$とIndirect effect $IE_{a,b}(Y)$に分解されます。式中の$Z$とはMediate variableといい、センシティブ情報とラベルの間に入る変数です。UC Berkleyの入試の例で言うとセンシティブ情報$A$がGender、ラベル$Y$はAdmission、そしてMediate variable $Z$はDepartmentに対応します。この$DE$と$IE$を比べることにより、差別があるかどうかを判定することができます。
因果推論に基づく公平性の問題点
上により、データに偏りがあっても公平がどうか判定できます。しかしこの手法は因果関係のグラフをきちんと作れるか、という所によっています。以下に、その例を列挙します
Direct effectがないということと差別がないということは別
仮にDirect effectがなかったとしても、Indirect effectが存在することすら問題になることはあります。たとえば、ある学部が女性差別的なポリシーを持っているために女性から選ばれなかった場合、それはIndirect effectしかなかったとしても問題になることはあります。
正しいMediate variableを見つけられるかはとても微妙
Mediate variableはかなずしも一つとは限りません。もしかすると男女で入学テストの成績に差があり、それが合格率の違いに影響しているのかもしれません。しかし、何もかもMediate variableとしてしまうと、本当にDirect efffectがあったときに見分けられなくなるかもしれません。
矢印の向きが微妙
因果推論において因果関係のグラフの矢印の向きはとても大事です。ある変数$Z$がMediate variableとなるためには$A \rightarrow Z \rightarrow Y$となる必要がありますが、果たして次の例はどうでしょうか。

ある宗教を信じていることが大学の合否に影響を与えている場合を考えましょう。このときに、その宗教を信じる人たちの教育レベルが低いことがMediate variableとなるのか(左側のグラフ)、それとも教育レベルが低い事によってその宗教を信じることになってしまうのか(右側のグラフ)、矢印の向きはとても曖昧です。この矢印の向きが異なると前の式は使えないので、どちらが正しいのかによって結果が変わってしまいます。
まとめ
以上見てきたとおり、まだまだ機械学習の公平性の議論は未熟なので、これからも研究の余地がありそうでした。いろいろな応用が出てきたらまた新しい公平性の議論も起こりそうなのでこれからも注目していきます。
