はじめに
@HppyCtrlEngnrng 氏の「Arduino Nanoで作る小さな制御理論実験環境」という記事の「手軽に実験できるシンプルでコンパクトな制御系」というコンセプトに感銘を受けました.
そこで当記事では,上記記事で紹介された制御系のネットワーク化を試みます.
今回ネットワーク化に取り組む理由は,研究対象として元々ネットワーク化制御系に興味があったためです.
ハードウェア
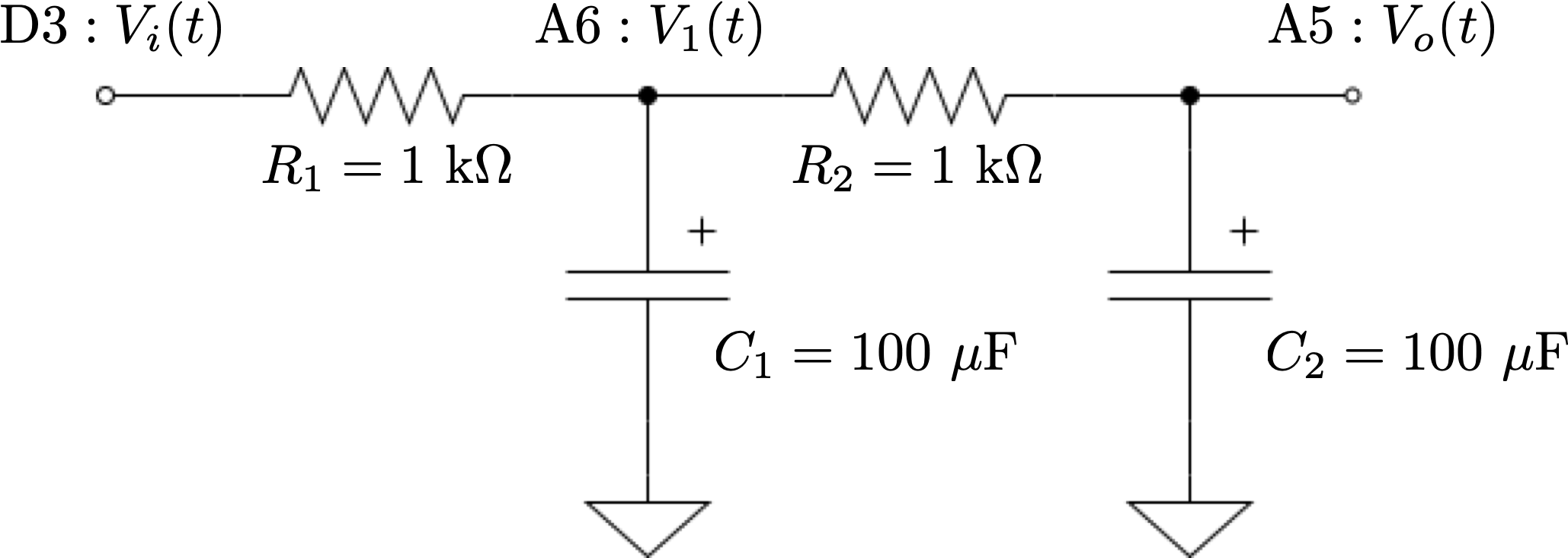
本記事で扱うハードウェアの外観及び回路図を以下に示します.
制御対象となる抵抗2個,コンデンサ2個からなる回路と Arduino nano は元記事様と共通です.
この制御対象の状態空間表現の一つは,下記のように表せます.
\frac{d}{dt}
\begin{bmatrix}
V_o[t]\\
V_1[t]
\end{bmatrix}
=
\begin{bmatrix}
-\frac{1}{C_2 R_2} & \frac{1}{C_2 R_2}\\
\frac{1}{C_1 R_2} & -\frac{1}{C_1}(\frac{1}{R_1}+\frac{1}{R_2})
\end{bmatrix}
\begin{bmatrix}
V_o[t]\\
V_1[t]
\end{bmatrix}
+
\begin{bmatrix}
0\\
\frac{1}{C_1 R_1}
\end{bmatrix}
V_i[t]
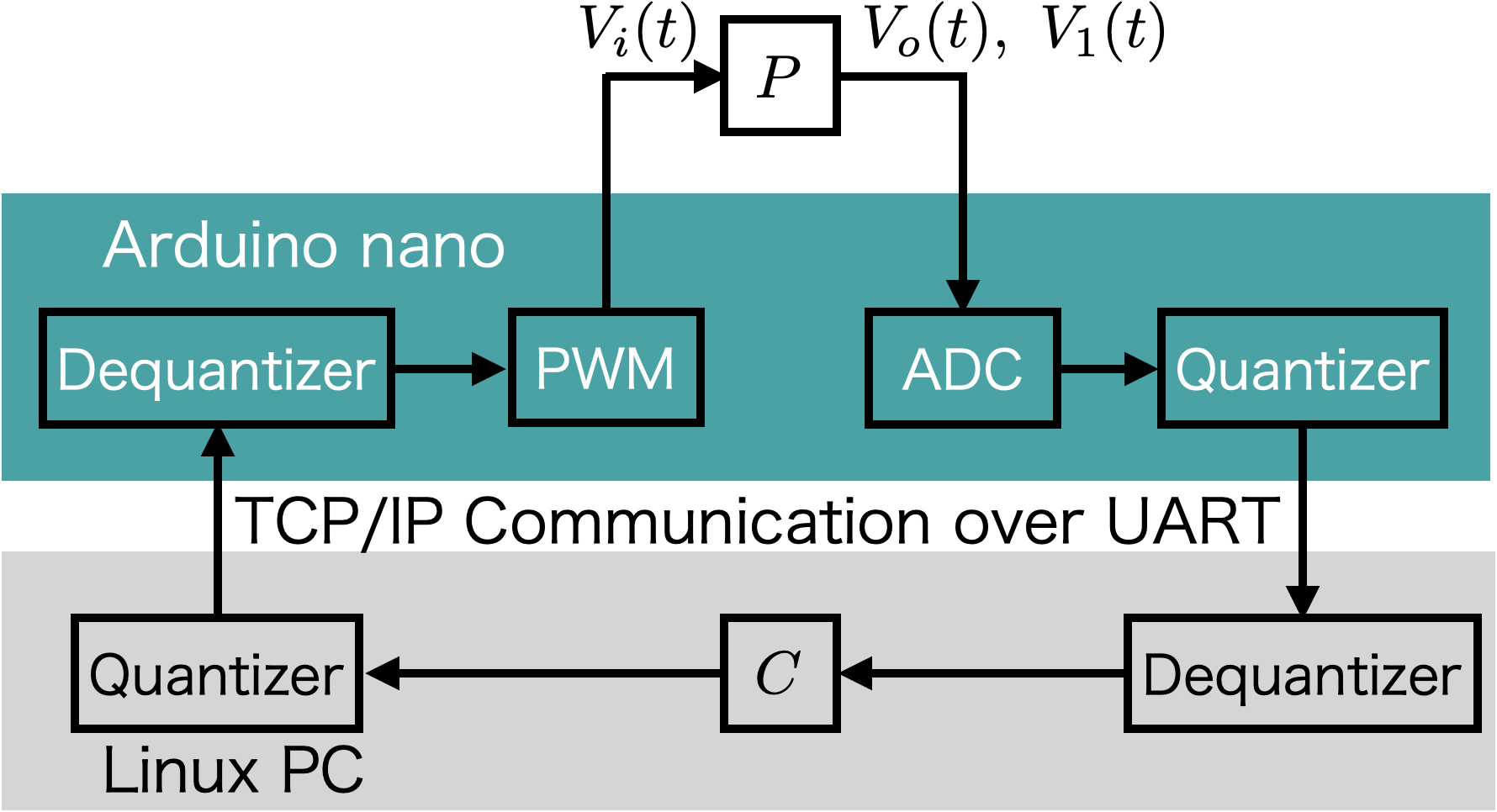
元記事様との相違点は,Arduino と USB 接続した PC もネットワーク上の制御器として,下記のように制御系に含まれる点です.
制御対象のモデル
オフラインでシステム同定をおこなった結果,下記のモデルを得ました.
\begin{bmatrix}
V_o[k+1]\\
V_1[k+1]
\end{bmatrix}
=
\begin{bmatrix}
0.951847 & 0.036224\\
0.0413406 & 0.583318
\end{bmatrix}
\begin{bmatrix}
V_o[k]\\
V_1[k]
\end{bmatrix}
+
\begin{bmatrix}
0.0115051\\
0.377747
\end{bmatrix}
V_i[k]
~~~\tag{1}
以下,モデルを利用して制御器を設計する際は,こちらのモデルを用いることとします.
ソフトウェア
当記事で紹介するソフトウェア群は,全てArduino_NW_Control リポジトリで公開しています.
利用方法はリポジトリの Readme をご覧ください.
Arduino_NW_Control は,Arduino に書き込むクライアントプログラム,および Linux マシン上で実行するサーバプログラムに大別されます.
- クライアントプログラムは,SerialIP ライブラリを使用します.
SerialIP は,uIP(8bit, 16bit マイコン向けの TCP/IP 実装 OSS)を Arduino IDE で利用するための Wrapper Library です. - サーバプログラムは,標準ライブラリで構成します.
Arduino はシリアルポートを介して Linux マシンに TCP/IP 接続するため,追加のハードウェアを一切用いることなく制御系をネットワーク化することができます.
(元記事のコンセプトを崩さないため,この点は拘りました.)
Arduino 側
Timer1 による定周期割り込みでサーバと通信し,制御するプログラム例を下記に示します.
(@HppyCtrlEngnrng 氏のコードをベースに改変しています.)
client プログラム例
# include <SerialIP.h>
# include <TimerOne.h>
// PIN Setting
# define INPUT_PIN 3
# define OUTPUT_PIN_1 6
# define OUTPUT_PIN_2 5
// This is the Control server to connect to. This default assumes an Control server
// on your PC. Note this is a parameter list, so use commas not dots!
# define CONTROL_SERVER 192,168,5,1
// IP and subnet that the Arduino will be using. Commas again, not dots.
# define MY_IP 192,168,5,2
# define MY_SUBNET 255,255,255,0
// Quantize Gain
# define Q_GAIN 48.0
// Because some of the weird uIP declarations confuse the Arduino IDE, we
// need to manually declare a couple of functions.
void uip_callback(uip_tcp_appstate_t *s);
typedef struct {
char input_buffer;
char output_buffer[2];
} connection_data;
uip_ipaddr_t control_server;
struct uip_conn *conn;
# define SET_IP(var, ip) uip_ipaddr(var, ip)
// State Variable
float V1, Vo;
// Input
float Vi;
// Convert ADC output to -2.5~2.5V
float convDac(float y){
return (y - 511) / 1023.0 * 5.0;
}
// Convert Voltage to PWM duty ratio
int convPwm(float u){
int ret = 255/5*u + 128;
if (ret > 255)
ret = 255;
else if (ret < 0)
ret = 0;
return ret;
}
void setup() {
Serial.begin(115200);
SerialIP.use_device(Serial);
SerialIP.set_uip_callback(uip_callback);
SerialIP.begin({MY_IP}, {MY_SUBNET});
SET_IP(control_server, CONTROL_SERVER);
Timer1.initialize(100000);
Timer1.attachInterrupt(open_port);
Timer1.start();
}
char quantizer(float sig){
return char(sig*Q_GAIN);
}
float dequantizer(char sig){
return float(sig/Q_GAIN);
}
void open_port() {
if(!uip_connected()){
conn = uip_connect(&control_server, HTONS(8000));
if (conn == NULL) {
return;
}
}
}
void loop() {
// Check the serial port and process any incoming data.
SerialIP.tick();
}
void uip_callback(uip_tcp_appstate_t *s)
{
if (uip_connected()) {
connection_data *d = (connection_data *)malloc(sizeof(connection_data));
s->user = d;
V1 = convDac(analogRead(OUTPUT_PIN_1));
Vo = convDac(analogRead(OUTPUT_PIN_2));
d->output_buffer[0]=quantizer(Vo);
d->output_buffer[1]=quantizer(V1);
PSOCK_INIT(&s->p, (uint8_t *)(&d->input_buffer),sizeof(&d->input_buffer));
}
// Call/resume our protosocket handler.
handle_connection(s,(connection_data *)s->user);
// If the connection has been closed, release the data we allocated earlier.
if (uip_closed()) {
if (s->user) free(s->user);
s->user = NULL;
}
}
int handle_connection(uip_tcp_appstate_t *s,connection_data *d)
{
PSOCK_BEGIN(&s->p);
// Send plant data over the connection.
PSOCK_SEND(&s->p,d->output_buffer,sizeof(d->output_buffer));
// Read control input into the input buffer we set in PSOCK_INIT. Data
// is read until the input buffer gets filled up.
PSOCK_READBUF(&s->p);
Vi=dequantizer(d->input_buffer);
analogWrite(INPUT_PIN, convPwm(Vi));
// Disconnect.
PSOCK_CLOSE(&s->p);
// All protosockets must end with this macro. It closes the switch().
PSOCK_END(&s->p);
}
割り込みで呼び出される open_port() は,Arduino がサーバと接続するだけという点にご注意ください.
実際にデータを送受信する処理は,loop() 内の SerialIP.tick() によって非同期的に少しずつ実行されます.
したがって,サーバとの通信がリアルタイムに完了することを実験前に確認しておく必要があります.
筆者は Linux PC 側で一定時間ログを取得し,取得できたログの数と時間の間に以下の関係が成り立つことをもって制御系が概ねリアルタイムであると確認しています.
\text{ログの数}=\frac{\text{計測時間}}{\text{制御周期}}
参考として実例を挙げると,私の環境(macbook pro 2018, VirtualBox 上の Ubuntu 20.04)では,
100 ms 周期だと余裕をもって通信が完了しますが,50 ms で制御するには一工夫が必要でした.1
Linux 側
Arduino の出力を受信し,制御入力を計算して送信する C プログラムの例を下記に示します.
server プログラム例
# include <stdlib.h>
# include <string.h>
# include <unistd.h>
# include <sys/fcntl.h>
# include <sys/types.h>
# include <sys/socket.h>
# include <netinet/in.h>
# include <arpa/inet.h>
# include <netdb.h>
# include <stdio.h>
// M-Series update width
# define MSEQ_WIDTH 120
// Quantize gain
# define Q_GAIN 48.0
void server(int sockfd);
int main(void){
int sockfd;
int new_sockfd;
unsigned int writer_len;
struct sockaddr_in reader_addr;
struct sockaddr_in writer_addr;
/* make socket */
if((sockfd = socket(PF_INET,SOCK_STREAM,0)) < 0){
perror("fail at make reader socket");
exit(1);
}
char *opt;
opt = "sl0";
if(setsockopt(sockfd,SOL_SOCKET,SO_BINDTODEVICE,opt,3) < 0){
perror("fail at setsocket opt");
exit(1);
}
/* Setting Communication Port, address */
bzero((char *) &reader_addr,sizeof(reader_addr));
reader_addr.sin_family=PF_INET;
reader_addr.sin_addr.s_addr=htonl(INADDR_ANY);
//reader_addr.sin_addr.s_addr=inet_addr("192.168.5.1");
reader_addr.sin_port=htons(8000);
/* bind addres to socket */
if(bind(sockfd, (struct sockaddr *)&reader_addr, sizeof(reader_addr)) < 0){
perror("fail at bind socket");
exit(1);
}
/* setting conect request */
if(listen(sockfd,5)<0){
perror("fail at listen");
close(sockfd);
exit(1);
}
while(1){
/* waiting conect request */
if((new_sockfd = accept(sockfd,(struct sockaddr *)&writer_addr,&writer_len)) < 0){
perror("fail at accept");
exit(1);
}
server(new_sockfd);
}
close(sockfd);
return 0;
}
// M-Series Conversion
char mseq(){
// シフトレジスタ
static unsigned char Xn = 1;
static unsigned int cnt = MSEQ_WIDTH;
unsigned ret;
cnt--;
ret = ((Xn & 64) >> 6) ^ (Xn & 1);
if (cnt == 0){
Xn = (Xn << 1) + ret;
cnt = MSEQ_WIDTH;
}
return ret;
}
char quantizer(float sig){
return (char)(sig*Q_GAIN);
}
float dequantizer(char sig){
return (float)(sig/Q_GAIN);
}
float control(float e){
return 1.0 * e;
}
void server(int sockfd){
char buf[8]={};
char write_buf[8]={};
float Vo,V1,Vr,Vi;
FILE *fp;
if(read(sockfd,buf,2) < 0){
close(sockfd);
return ;
}
Vr = 4.0 * (mseq() - 0.5);
Vo=dequantizer(buf[0]);
V1=dequantizer(buf[1]);
Vi=control(Vr-Vo);
printf("%f,%f,%f,%f\n",Vr,Vo,V1,Vi);
write_buf[0]=quantizer(Vi);
if(write(sockfd,write_buf,1) < 0){
close(sockfd);
return ;
}
if((fp=fopen("data.csv","a")) != NULL){
fprintf(fp,"%f,%f,%f\n",Vr,Vo,V1);
fclose(fp);
}
close(sockfd);
}
上記 C プログラムを実行する前に,PC のネットワークインターフェースと Arduino のシリアルポートを slattach コマンドで紐づける必要があります.
下記スクリプトを sudo 権限で実行してください.
# !/bin/sh
FILE="data.csv"
if [ -f $FILE ];then
rm $FILE
fi
ps -a | grep slattach | awk '{print $1}' | xargs kill
slattach -L -s 115200 -p slip /dev/ttyUSB0&
sleep 1s
ifconfig sl0 192.168.5.1 dstaddr 192.168.5.2
ifconfig sl0 netmask 255.255.255.0
./ControlServer
使用例
本環境の制御対象を以下の離散時間モデルで表します.
\begin{align}
x[k+1]&=Ax[k]+Bu[k]\\
y[k]&=Cx[k]
\end{align}
~~~\tag{2}
ただし,
x[k]=
\begin{bmatrix}
V_o[k]\\
V_1[k]
\end{bmatrix}
とします.
以下に,本環境を使用した実験の例を示します.
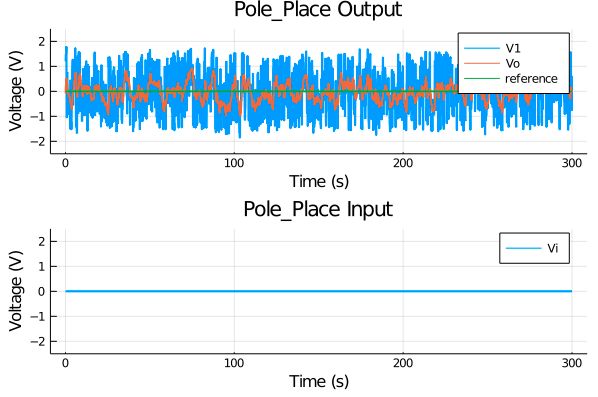
状態フィードバック制御
同定した離散時間モデル(1)を用いて,極を0.75±j0.1 に配置する状態FB制御器は
V_i[k]=-
\begin{bmatrix}
2.9145 & 0.0043
\end{bmatrix}
\begin{bmatrix}
V_o[k]\\
V_1[k]
\end{bmatrix}
で与えられます.
実験でレギュレータの効果を確認するため,入力端外乱$V_n\in[-2.0,2.0]$を印加します.
- Server 側
float control(float Vo, float V1){
return -2.9145*Vo - 0.0043*V1;
}
- Client 側
int handle_connection(uip_tcp_appstate_t *s,connection_data *d)
{
PSOCK_BEGIN(&s->p);
PSOCK_SEND(&s->p,d->output_buffer,sizeof(d->output_buffer));
PSOCK_READBUF(&s->p);
Vi=dequantizer(d->input_buffer);
analogWrite(INPUT_PIN, convPwm(Vi+random(-20,21)/10.0));
PSOCK_CLOSE(&s->p);
PSOCK_END(&s->p);
}
ネットワーク化制御系においては,制御対象および制御器が入出力信号をやり取りするために量子化をおこなう必要があります.
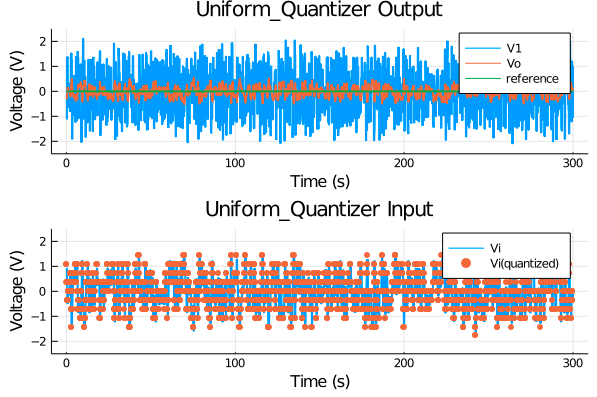
本節では,一様量子化器と対数型量子化器を用いて実験しました.
一様量子化器を用いた場合
量子化領域 ±3.0 を2^3-1 個(3 bit)の信号で量子化する例を下図に示します.
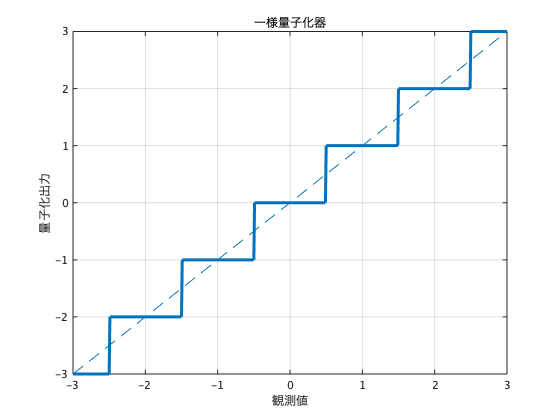
一様量子化器は,上図のように量子化領域を等間隔に分割するため,量子化誤差の大きさが一定です.
# define U_GAIN 48.0
# define U_MIN -128
# define U_MAX 127
char Uni_quantizer(float u){
char v=(char)(u*U_GAIN);
if(v>U_MAX){
v=U_MAX;
}else if(v<U_MIN){
v=U_MIN;
}
return v;
}
float Uni_dequantizer(char v){
float u=(float)v/U_GAIN;
return u;
}
実験では,データレート(通信1回あたりの伝達情報量)を 8 bitとし,量子化領域 ±2.5 V を量子化しました.
以下に制約なしの場合と状態FBをおこなった場合の時系列信号を示します.
状態FBをおこなった場合は,そうでない場合と比較すると外乱への感度が低減されています.
次に,制御器から Arduino への通信路のみデータレートを半分の 4 bitとした場合(量子化器を粗くした場合)のコードおよび時系列信号を示します.
# define U_GAIN 2.8
# define U_MIN -7
# define U_MAX 7
時系列信号を見ると,8 bit の場合と同様に概ね外乱を抑制できていることがわかります.
しかし,制御性能の指標として3000ステップの誤差のL2ノルム値を比較してみると,4 bit 一様量子化器の値が若干悪化しています.これは,量子化器を粗くしたために量子化誤差が大きくなったことが原因として考えられます.
| 制御手法 | L2ノルム [V] |
|---|---|
| 極配置法(8 bit一様量子化器) | 10.772 |
| 制御なし | 21.317 |
| 極配置法(4 bit一様量子化器) | 12.207 |
対数型量子化器を用いた場合
前項で確認したように,制御系のデータレートを下げると量子化器を粗くせねばならず,制御性能の劣化を招いてしまいます.
そこで,限られたデータレートで制御対象を安定化する手法として,対数型量子化器が提案されています[1][2].
対数量子化器$v=q(u)$は,下記の式で定義されます.
q(u)=
\left\{
\begin{array}{ll}
v_i, & \text{if}~~\frac{1}{1+\delta}v_i<u<\frac{1}{1-\delta}v_i,u>0,\\
0, & \text{if}~~u=0,\\
-q(-u), & \text{if}~~u<0
\end{array}
\right.
ここで,量子化器の出力$v_i\in V$は量子化器の粗さ$0<\delta<1$によって下記のように与えられます.
V=\left\{\pm v_i=
\Biggl(
\frac{1-\delta}{1+\delta}
\Biggr)^{i}v_0,
~i=0,\pm 1,\pm 2,\dots
\right\}\cup\{0\}
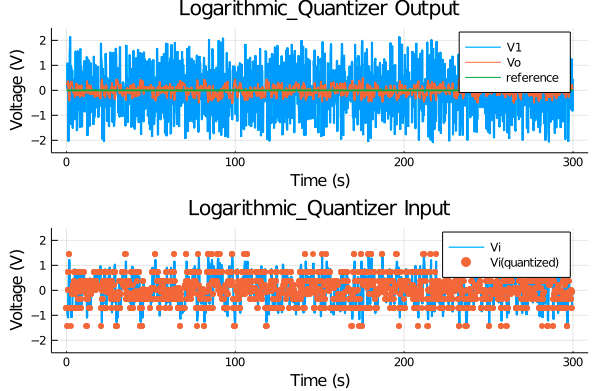
$v_0=1,~\delta=\frac{1}{3}$とした時,量子化領域 ±3.0 を2^3-1 個の信号で量子化する例を下図に示します.
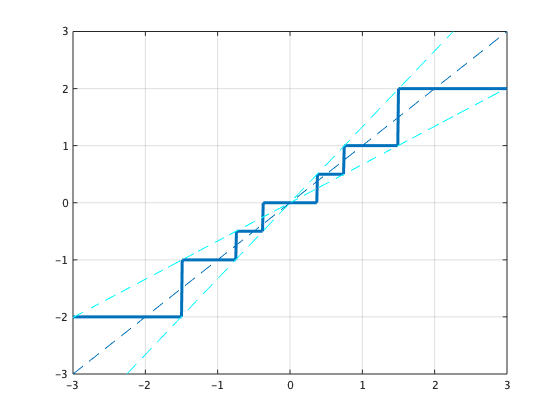
※軸のラベルを書き損ねましたが,横軸が観測値,縦軸が量子化出力です.
対数型量子化器は,上図のように原点(or 目標値)近傍は細かく,原点から遠方は粗く値を丸めるため,量子化誤差が不定という特徴があります.
本項は前項の結果と比較するため,Arduino から制御器への通信路は 8 bit の一様量子化器を用い,制御器から Arduino への通信路に 4 bit の対数量子化器を用います.
# define L_GAIN 2.8
char Log_quantizer(float u){
if(u<0.0){
return 15-Log_quantizer(-u);
}else{
float ug=u*L_GAIN;
if(ug<0.09375)
return 8;//v=8 means 0.0
else if(ug<0.1875)
return 9;//v=9 means 0.125
else if(ug<0.375)
return 10;//v=10 means 0.25
else if(ug<0.75)
return 11;//v=11 means 0.5
else if(ug<1.5)
return 12;//v=12 means 1.0
else if(ug<3.0)
return 13;//v=13 means 2.0
else if(ug<6.0)
return 14;//v=14 means 4.0
else
return 15;//v=15 means 8.0
}
}
float Log_Dequantizer[16]={-8.0,-4.0,-2.0,-1.0,-0.5,-0.25,-0.125,-0.0,
0.0,0.125,0.25,0.5,1.0,2.0,4.0,8.0};
int handle_connection(uip_tcp_appstate_t *s,connection_data *d)
{
PSOCK_BEGIN(&s->p);
PSOCK_SEND(&s->p,d->output_buffer,sizeof(d->output_buffer));
PSOCK_READBUF(&s->p);
Vi=Log_Dequantizer[d->input_buffer]/2.8;
analogWrite(INPUT_PIN, convPwm(Vi+random(-20,21)/10.0));
PSOCK_CLOSE(&s->p);
PSOCK_END(&s->p);
}
以下に対数型量子化器を用いた状態FBの実験結果を示します.
出力の時系列信号を見ると,一様量子化器を用いた場合と同様,概ね外乱を抑制できていることがわかります.
また制御入力の時系列信号を見ると,一様量子化器を用いた場合と比較し,信号が原点付近に集中して丸められていることがわかります.
さらに,このときの誤差のノルムは10.822 でした.
再掲ですが,他の実験結果と比較すると下記の通りです.
| 制御手法 | L2ノルム [V] |
|---|---|
| 極配置法(8 bit一様量子化器) | 10.772 |
| 制御なし | 21.317 |
| 極配置法(4 bit一様量子化器) | 12.207 |
| 極配置法(4 bit対数型量子化器) | 10.822 |
8 bit の一様量子化器を用いた場合と比較しても 1% 程度しかノルム値の増大は見られませんでした.
これは,「目標値近傍を細かく,遠方を粗く」丸める対数型量子化器の特徴により,原点近傍の小さな制御入力の量子化誤差を抑えられたためだと考えられます.
以上から対数型量子化器を用いた場合,データレートを 4 bit に抑えつつ,8 bit の一様量子化器と同程度に外乱を抑制しうることがわかりました.
積分型コントローラ
前節ではレギュレータ問題を扱いましたが,本節ではサーボ問題を考えます.
式(2)に対し,次式のような拡大系を考えます.
\begin{bmatrix}
x[k+1]\\
x_{i}[k+1]
\end{bmatrix}
=
\begin{bmatrix}
A & \bf{\it{0}}\\
1 & 0
\end{bmatrix}
\begin{bmatrix}
x[k]\\
x_{i}[k]
\end{bmatrix}
+
\begin{bmatrix}
B\\
0
\end{bmatrix}
u[k]+
\begin{bmatrix}
\bf{\it{0}}\\
-r
\end{bmatrix}
$x_{i}$は,状態変数$V_o$の積分値,$r$は,$V_o$の目標値です.
このとき,制御入力$u[k]=V_i[k]$を次の式で与える時,
V_i[k]=-
\begin{bmatrix}
f & f_{i}
\end{bmatrix}
\begin{bmatrix}
x[k]\\
x_{i}[k]
\end{bmatrix}
同定した離散時間モデル(1)を用いて極を0.75±j0.1, -0.02 に配置すると,
f=-
\begin{bmatrix}
1.2460 & 0.1081
\end{bmatrix}
,~~f_i=1.6422
となります.
float control(float Vo, float V1,float Vr){
static float Ve = 0.0;
Ve += (Vo-Vr)*100e-3;
/* pole place @ 0.75+0.1i, 0.75-0.1i, -0.02 */
return -1.2460*Vo - 0.1081*V1 - 1.6422*Ve;
}
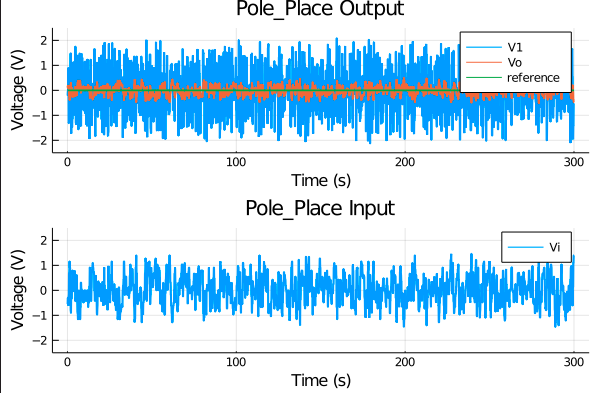
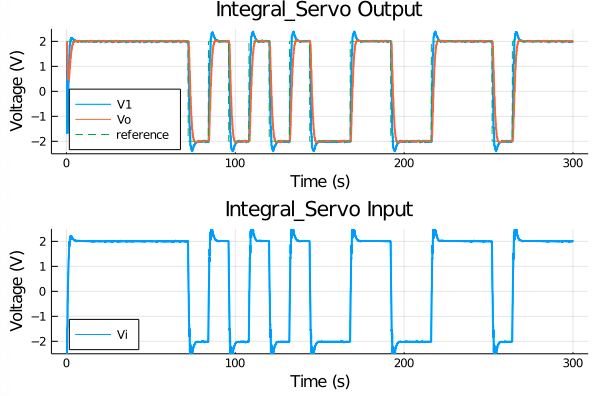
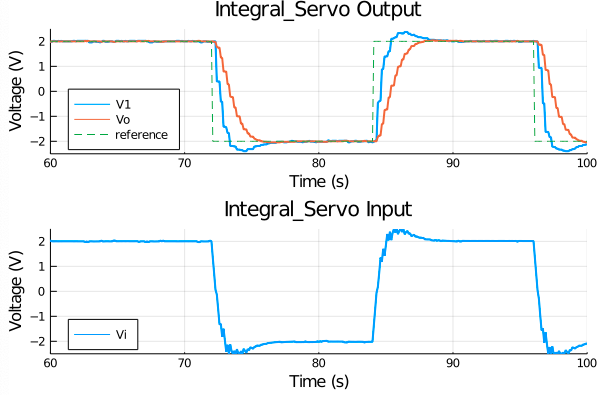
こちらの制御器を用いた実験結果と,その一部を拡大したグラフを下記に示します.
時系列信号を見ると積分動作によって,目標値へ良好に追従できていることがわかります.
ただし,制御入力がピークでわずかに飽和してしまっているようです..
(おまけ)モデル予測制御
ネットワーク化制御系の利点の一つとして,制御系から離れた場所にある豊富な計算資源を制御に利用できる点が挙げられます.
本節では折角なので,MATLAB の Model Predicting Control Toolbox を使って制御を試みます.
まず,Arduino と TCP/IP 通信しつつモデル予測制御をおこなうコードを下記に示します.
matlab コード例
clear all;
Q_GAIN=48;
Ts=300e-3;
time=300;
plotting=1;
x=Ts:Ts:time;
len=length(x);
Vo=zeros(len,1);
V1=zeros(len,1);
Vi=zeros(len,1);
Vr=zeros(len,1);
for i=1:len
Vr(i)=4*(Mseq()-0.5);
end
%%
%Create Model Predict Controller
A = [ 0.951847 0.036224;0.0413406 0.583318];
B = [ 0.011505;0.377747];
C = [1 0;0 1];
D = 0;
CSTR = d2d(ss(A,B,C,D,0.1),Ts);
CSTR.InputGroup.MV = 1;
CSTR.OutputGroup.MO = 1;
MPCobj = mpc(CSTR,Ts);
MPCobj.PredictionHorizon = 15;
MPCobj.MV.Min = -2.5;
MPCobj.MV.Max = 2.5;
MPCobj.MV.RateMin = -1;
MPCobj.MV.RateMax = 1;
MPCobj.W.ManipulatedVariablesRate = 0.3;
MPCobj.W.OutputVariables = [1 0;0 1];
mpc_state = mpcstate(MPCobj);
%%
% Create tcpip object(note that this function will be removed)
sock=tcpip('192.168.5.2',8000,'NetworkRole','server');
if plotting==1
% Create Output Signal Figure
haxes1=subplot(2,1,1);
h1=animatedline(haxes1,'MaximumNumPoints',len*2);
axis([0 time -3 3])
title(haxes1,'Output Signal')
grid on
% Create Input Signal Figure
haxes2=subplot(2,1,2);
h2=animatedline(haxes2,'MaximumNumPoints',len*2);
axis([0 time -3 3])
title(haxes2,'Input Signal')
grid on
end
% Control Loop
for k=1:len
% Open tcpip
fopen(sock);
% Read message
read_buffer=fread(sock,2,'int8');
Vo(k)=read_buffer(1)/Q_GAIN;
V1(k)=read_buffer(2)/Q_GAIN;
Vi(k)= mpcmove(MPCobj,mpc_state,[Vo(k) V1(k)],[Vr(k) Vr(k)]);
disp([Vr(k) Vo(k) V1(k) Vi(k)]);
% Send Voltage Input
fwrite(sock,Vi(k)*Q_GAIN,'int8');
% Close tcpip
fclose(sock);
if plotting==1
addpoints(h1,x(k),Vo(k));
addpoints(h1,x(k)+Ts,Vo(k));
addpoints(h2,x(k),Vi(k));
addpoints(h2,x(k)+Ts,Vi(k));
drawnow limitrate
end
end
ただし,MATLAB の tcpip 関数がやや低速なため,制御周期を 300 (ms) で設定しています.
また,制御入力 $Vi$ の拘束条件を ±2.5 (V)に設定します.
さらに,折角なので1ステップあたりの制御入力の変化量を 1 (V) 以内に収めるよう設定してみます.
さいごに予測ホライズンは,15ステップに設定しました.
上記コードを実行するには,以下のスクリプトを sudo 権限で実行します.
ps -a | grep slattach | awk '{print $1}' | xargs kill
sudo slattach -L -s 115200 -p slip /dev/ttyUSB0&
sleep 1s
sudo ifconfig sl0 192.168.5.1 dstaddr 192.168.5.2
sudo ifconfig sl0 netmask 255.255.255.0
matlab -nosplash -nodesktop -r 'ControlServer'
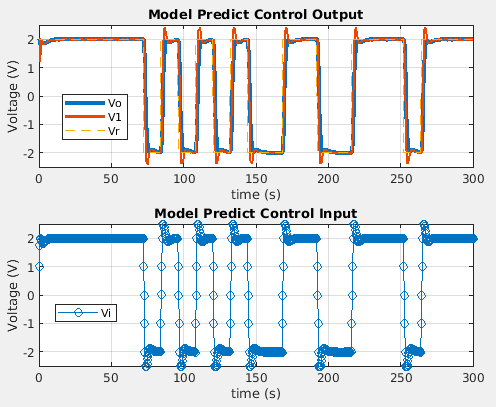
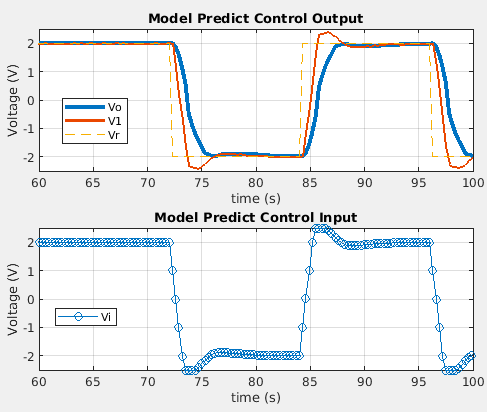
以下に,モデル予測制御の実験結果と,その一部を拡大したグラフを以下に示します.
出力 $V_o$ は目標値 $V_r$ に概ね追従できており,良好な応答が得られています.
また,制御入力 $Vi$ は最大でも 1 (V) 刻みで変化し,常に± 2.5 (V)に収まっているため,指定した拘束条件を満たしつつ制御を達成していることがわかります.
参考文献
[1]Stabilization of Linear Systems With Limited Information, N.Elia and S.K.Mitter 2001
[2]対数型動的量子化器の解析と設計, 杉江 and 岡本, 2009
[3] Serial HOWTO
-
当記事で紹介する実験環境で一番のボトルネックはシリアル通信上の TCP/IP 通信です.したがってシリアル通信の設定をより高速にすることで,制御周期を上げることができます. しかし slattach は古いコマンドのため, 115200 bps 以下しかサポートしていません.そこでより高速な通信レートを適用するには,別途 setserial コマンドの spd_cust オプションで slattach コマンドを騙してやる必要があります[3]. ↩