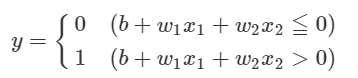記事を書くに至った経緯
ゼロから作るDeeplearning１では非線形分離問題としてXOR回路を扱っており、単純パーセプトロンを2層にすることで解くことができると書かれている。
ただ、非線形領域は2層以上のパーセプトロンで表現できることに少しギャップを感じた。そこで、2層のパーセプトロンで曲線のような非線形な領域を表現できることを図で表現してみたいと考え、この記事を書くに至りました。
線形な領域と非線形な領域
単純に言うと直線で分離可能かどうかである
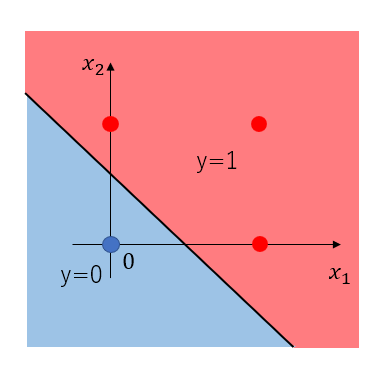
以下の図は赤と青の点は直線で分離できる、分離した領域は線形な領域
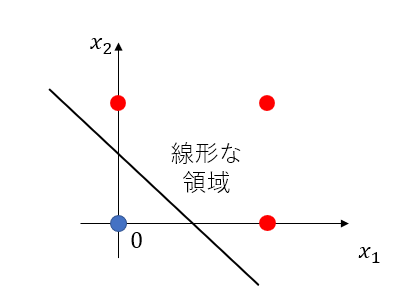
以下の図は赤と青の点は直線で分離できない、そのため分離した領域は非線形な領域となる
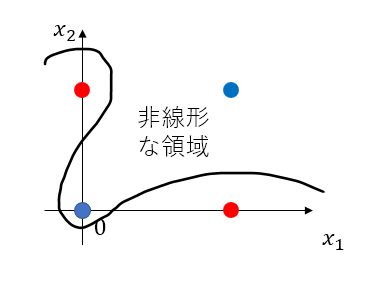
パーセプトロンの限界
パーセプトロンは、複数の信号入力として受け取り、ひとつの信号を出力します。
パーセプトロンを数式で表すと、以下のようになる
パーセプトロンはこのように1本の直線で分けた線形な領域は表現できるが。非線形の領域を表現できない。このことをパーセプトロンの限界といいます
パーセプトロンを2層重ねることで非線形な領域を表現する
そこで、XORゲート問題について扱う
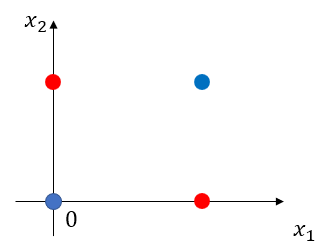
この赤と青を分離することを考える
以下のように2つのパーセプトロンを重ねることで分離することができる(それぞれの座標を代入すると分離できることを確認できると思います）
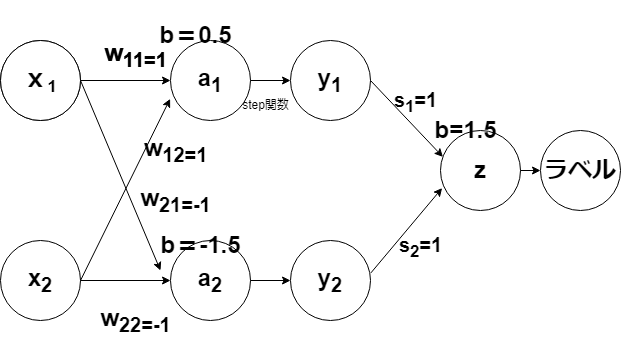
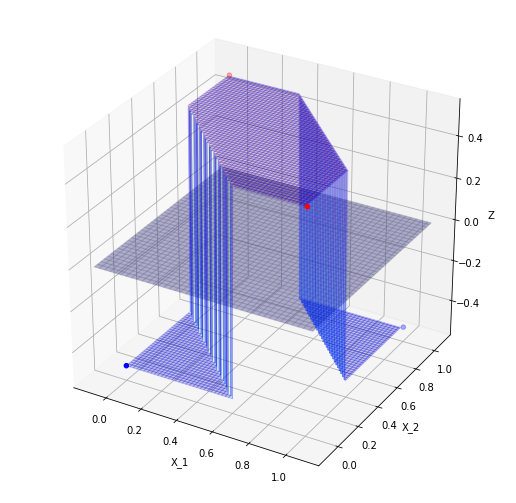
二つの特徴量とｚの関係を可視化すると、
二次元上の点を二つの単純パーセプトロンによってもう一つの次元（z軸）に写像し、
z軸の値で線形分離することを考えると
zの値を0以下はnegative 0以上はpositiveとするとXOR回路を表現できたことになる
つまり、2つの線形分離で重なる部分が非線形な領域となっている
ただ、単に直線を2つ引いて重なる部分をy=1としているだけである
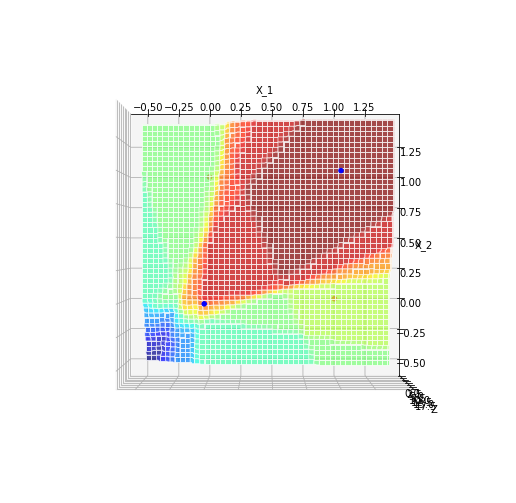
先ほど紹介した曲線のような分離境界線は本当に引けるのかと疑問に思ったため、その様子を実際に可視化してみました
曲線のような非線形領域も単純パーセプトロンの重ね合わせを用いて表現できるのか
分離境界線としたい曲線の接線をパーセプトロンで表現し、それらを組み合わせることで曲線のような非線形な領域を表現できるのではないかと考えた
ただ、この曲線を式で表現することが難しかったため、その曲線の接線ぽい直線をパーセプトロンで表現することにする
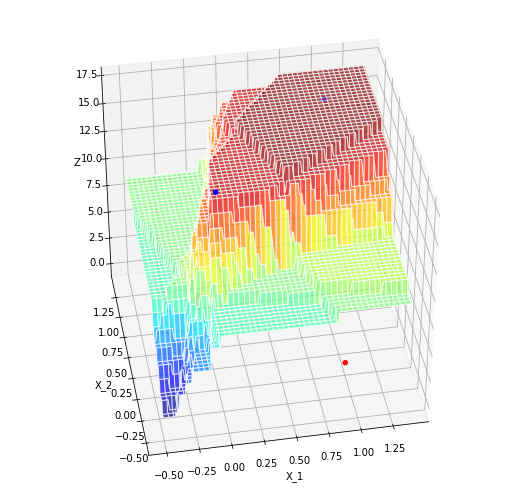
それぞれの直線をパーセプトロンで表し、その出力を入力としたすべての重みs=1のパーセプトロンを考える
二つの特徴量とｚの関係を可視化すると、
この図を上から見てみると、
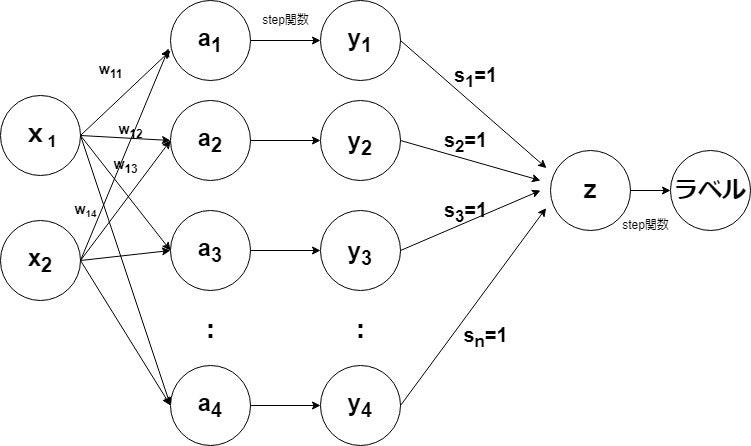
黄色い部分が曲線のような非線形領域の分離境界線となっていることがわかる
終わりに
パーセプトロンの組み合わせを変えるとどんな関数でも近似できるなぁと実感しました。
パーセプトロンを無駄遣いしている気もしますが、、
また勉強会で気になった点などを書いていきたいです！
参考文献
ゼロから作るDeeplearning-Pythonで学ぶディープラーニングの理論と実装 著者 斎藤 康毅
パーセプトロンを多層にするとなぜXOR回路を表現できるのか- https://ker60.hatenablog.com/entry/2017/06/13/000609
ニューラルネットワークが任意の関数を表現できることの視覚的証明 - https://nnadl-ja.github.io/nnadl_site_ja/chap4.html