More than 1 year has passed since last update.

【ゼロつく勉強会　＃3 記録】

Last updated at 2022-12-07Posted at 2022-12-07

はじめに

AcademiXでは、ゼロから作るdeeplearning１を参考図書とし、勉強会を行っています。毎回の勉強会に3－5人程度参加していただいており、人数は少ないのですが踏み込んだ話ができてとても充実しています。今回は勉強会で出た質問・興味深かった点などをメモ代わりに記事にまとめてみました！

勉強会

勉強会は代表者が担当章を説明し、それに対して質問や議論を行っています。今回は第4章のニューラルネットワークの学習についてAcademiXのメンバーのTさんに発表していただきました。
さっそく書いていきます！！

興味深かった点 (Tさんの発表）

バッチサイズを作成する際、無作為抽出している! 重複が生じる！？

以下が、ゼロつくに載っているミニバッチを製作するコードです

for i in range(iters_num):
    # ミニバッチの取得
    batch_mask = np.random.choice(train_size, batch_size)
    x_batch = x_train[batch_mask]
    t_batch = t_train[batch_mask]

x_train(t_train)から抽出するミニバッチのindexをnp.random.choiceによって取得している
np.random.choiceは重複選択を許すランダム選択方法 ミニバッチ内・間でデータの重複が起こると指摘していただきました！！（全く気が付きませんでした、、、）

デフォルトの手法は、2点の問題点が考えられる。

np.random.choiceは重複選択を許すランダム選択方法なので、ミニバッチ内でデータの重複が起こり、学習するデータに偏りが生じる恐れがある。

イテレーションごとに毎回make_batchでランダムに選択(np.random.choice)しているので、ミニバッチはバッチを重複せずに分割したものという特徴に反して、ミニバッチ間でデータの重複が発生し、学習するデータに偏りが生じる恐れがある。
(Tさんの発表資料から引用）

さらに重複を生じない方法も実装して、従来の方法と比較していただきました!!

ミニバッチ作成処理　改良版

実装内容
epochの中で、ミニバッチ内、ミニバッチ間でデータの重複や偏りがなくなるように、1epochごとにランダムシャッフルしたインデックスのリストをバッチサイズごとに分割(Tさんの発表資料から引用）

def make_batch_mask_list(train_size, batch_size):
    """epochごとにbatchのmaskを作成する"""
    idx_list = np.arange(train_size)
    np.random.shuffle(idx_list) # indexをシャッフル
    batch_mask_list = []
    for i in range(0, train_size, batch_size):
        batch_mask = idx_list[i:i+batch_size]
        batch_mask_list.append(batch_mask)

    return batch_mask_list


for i in range(iters_num):
    # ミニバッチの取得
    # batch_mask = np.random.choice(train_size, batch_size)
    if i % iter_per_epoch == 0:
        batch_mask_list = make_batch_mask_list(train_size, batch_size)
        batch_count = 0

    batch_mask = batch_mask_list[batch_count]
    batch_count += 1
    x_batch = x_train[batch_mask]
    t_batch = t_train[batch_mask]

両方の精度比較

	train_accuracy	val_accuracy
改善前	0.9477	0.945
改善後	0.9472	0.9449

ほとんど変化なかったそうです、、

精度に差があるほど、影響していない
どのサンプルデータも選択される確率は同じなので，十分な epoch でまわせば(結果として)大差ないのではないか、

色々考察できて面白かったです！！

epoch, iter, batchsizeの意味

epoch : データすべてをモデルに一回入力する処理
iter(iteration) : 1epoch完了するのにかかるbatch数
batch size : ミニバッチに含まれるデータ数、ミニバッチの大きさ

機械学習を学んでると英語の用語ばかり出てきて、ごちゃごちゃになりません、、
このように言葉の意味をまとめてくださると言葉の定義を曖昧のままにする僕にとっては非常にありがたいです！

話題になったこと

なぜ数値計算の方が誤差逆伝播法よりも計算が速くなるのか？

実際、数値微分でmodelを動かすと、学習するのに数時間かかったそうです。
議論の中で出た意見

数値微分では勾配を計算するのに勾配を求めたいパラメータ以外を固定し、モデル全体を用いて計算し求める。それをすべてのパラメータで行う必要があるため非常に時間がかかるのでは？
誤差逆伝播法はそれぞれの変数に関する偏微分を解析的に用意しておき。そこに代入するだけで勾配が求められるようになっている？
誤差逆伝播法では勾配を使いまわせる
テンソルが使われるから

いろんな意見が出ました！

この話題で20分ぐらい話していました。
結論、誤差逆伝播法をやらないとわからないよねっと、、来週に持ち越しになりました。

np.sum のkeepdimとは何か？

softmax関数でbatch内で各データごとに演算するとき、batchの次元を保持するために、keepdim=Trueとなっている。

def softmax(x):
    x = x - np.max(x, axis=-1, keepdims=True)   # オーバーフロー対策
    return np.exp(x) / np.sum(np.exp(x), axis=-1, keepdims=True)

次元を保持するイメージがわかなかった(後ほど調べてみた）
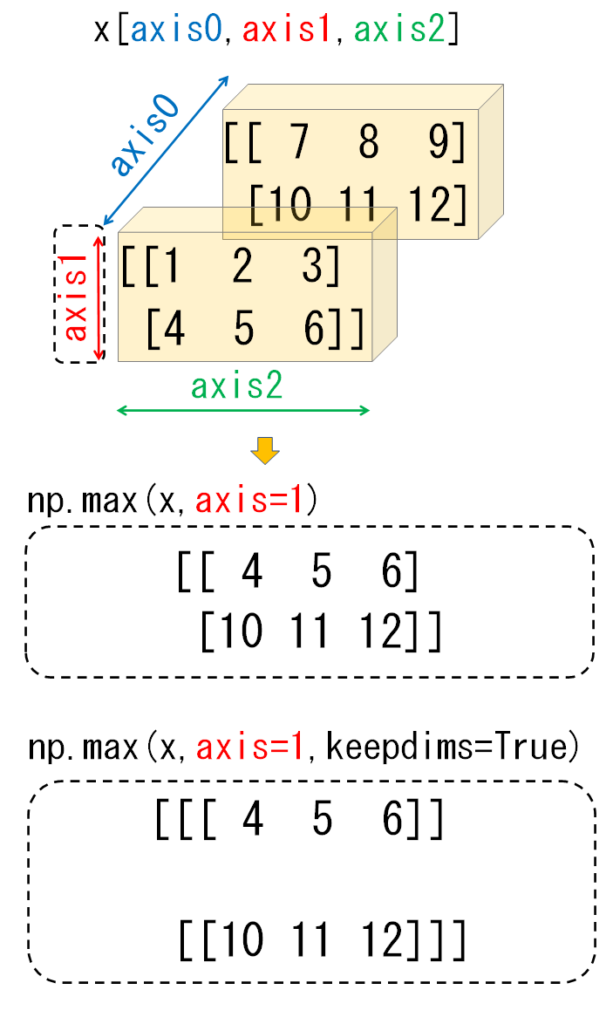
指定したaxis方向で値を集約すると、その集約した方向の次元は1になる。その時、その次元を削除するか、しないかの違い。
参考にした記事の図がわかりやすかったので載せておきます！！

引用）https://snowtree-injune.com/2020/05/03/keepdims-z006/

まとめ

いかがだったでしょうか、いつもこのような感じで、勉強会をしています！
勉強会の雰囲気が少しでも伝わればうれしいです！今後もゼロつく勉強会を開催していく予定ですので、興味がある方はぜひ、

Tさん発表ありがとうございました。

↓AcademiXのホームページ
https://www.academix.jp/

参考文献

ゼロから作るDeeplearning-Pythonで学ぶディープラーニングの理論と実装　著者　斎藤康毅
【なぜ】誤差逆伝播法が数値微分より高速な理由について「完全に理解した」のでまとめてみた
(https://www.chickensblog.com/backpropagation-why/)
NumPy♪関数maxやsumにおけるkeepdims指定の図解
(https://snowtree-injune.com/2020/05/03/keepdims-z006/)

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up

【ゼロつく勉強会 ＃3 記録】