サーバエンジニアにも、わかりやすく機械学習の教師あり学習（Supervised Learning）を理解してみた2

パーセプトロン

パーセプトロンとは、アルゴリズムであり、古のものであり、
機械学習を学ぶ上で知っておいたほうがいいことになります。

単純パーセプトロン

例えば、人気フォロワーを算出するようにします。
その際の指標をyoutubeのチャンネル登録数、twitterのフォロワー数するとしましょう。

例えば、

ユーザ名	チャンネル登録数	人気(ある場合1)
aaa	50	0
bbb	10000	0
ccc	100000	1
ddd	90000	0
eee	120000	1

ユーザ名	twフォロワー数	人気(ある場合1)
aaa	100	0
bbb	10	0
ccc	7000	1
ddd	150000	1
eee	90000	1

この場合、◯がcccさんとeeeさんなので、だいたい以下のような境界で人気化どうかがわかるようになります

どちらも人気があれば、人気と見なすことにします。
上記で言えば、
cccさんとeeeさんが人気ということになります。

この場合、境界を作ることによって、人気か不人気かわかるようになっています。

この区分け実際のプログラムで作るには、w=重みづけ、theta=バイアス（傾き加減）
をだいたい値で調整し、0,1で割り振れるようにします（図で言うと◯×）
チャンネル数 = w1 = 1.6
twフォロワー数 = w2 = 0.11
そして、その0,1の閾値を160500としましょう
ん、、どうやってこの値を求めたかですが、
適当にあたりをつけていくしかありません。
まずは、tmpの値を求めて、それが、0にくるのか1なのかを
判定できる。閾値を仮で設定し、もしそれが正しくなければ
w1,w2,thetaを微調整していく感じです。
この手作業が大変なのは、パーセプトロンの大変なところでもあります。

def AND_famous(x1,x2):
    w1 = 1.6
    w2 = 0.11
    theta = 160500
    tmp = w1*x1 + w2*x2
    
    if tmp <= theta:
        y = 0
    else:
        y = 1
    return y

print(AND_famous(50,100))
print(AND_famous(10000,10))
print(AND_famous(100000,7000))
print(AND_famous(90000,150000))
print(AND_famous(120000,90000))

//console結果
0
0
1
0
1

単純パーセプトロンでは、直線一つでグループ分けできる分類を分けることができます。

多層パーセプトロン

上記の場合にできないケースがあります。例えば、こんな結果だったらどうしますか？

1芸のみ秀でている人を判定します（2芸は含まない）
判定基準は、どちらかが当てはまれば天才(XOR)とします
参考）
https://wwws.kobe-c.ac.jp/deguchi/sc180/logic/gate.html
https://the01.jp/p0004619/

ユーザ名	テストの点数（3,4が正常）	才能(ありの場合1)
aaa	3	0
bbb	70	0
ccc	92	1
ddd	6	0
eee	97	0

ユーザ名	絵画の能力値（100最大）	才能(ありの場合1)
aaa	100	1
bbb	40	0
ccc	98	1
ddd	92	1
eee	70	0

この場合、どちらかのみ秀でているのは、
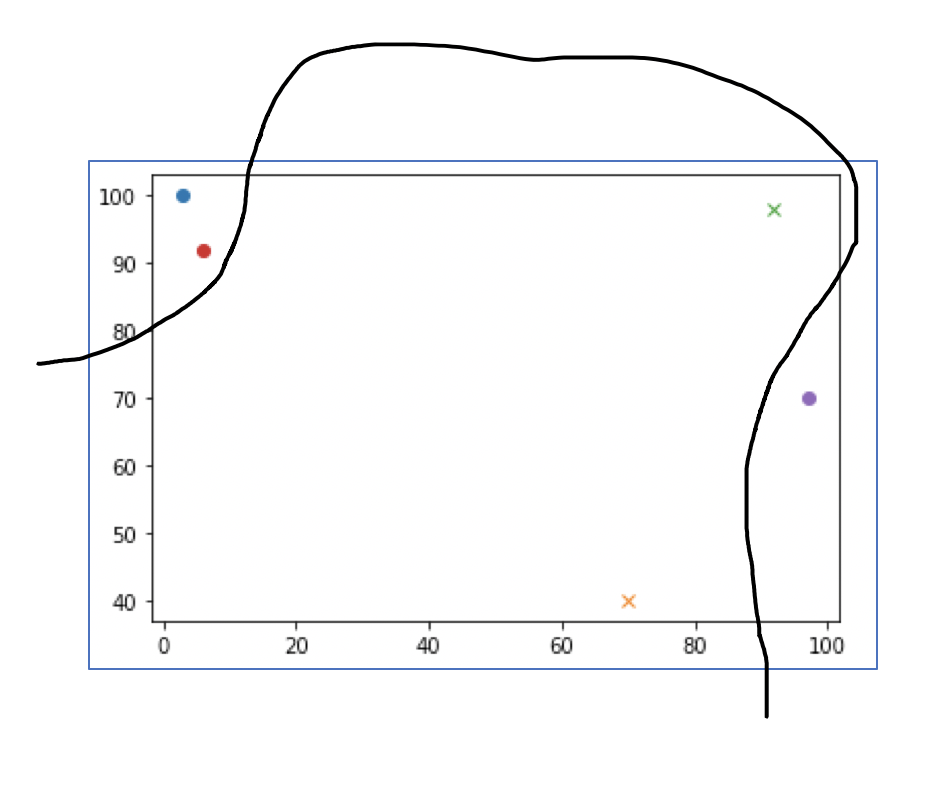
aaa,ddd,eee になります。図にすると以下になります

上の図を見て、○とxで分類しにいくなぁと思うと思います。
実際にグルーピングの線を引くとこんな感じになります。
これは、今回はプログラムは出しませんが、単純パーセプトロンを連結させることにより実現が可能であるとだけ覚えておくと良いでしょう

まとめると、
単純パーセプトロンは直線で0,1の境界線を引くことができる
多重パーセプトロンは曲線で0,1の境界線を引くことができる、ただし単純パーセプトロンを組み合わせられるものだけに限る
になります。

では、パーセプトロンで全てができるのかというとそうではありません。
例えば、

• 境界が閉じているもの
• 境界が複数あるもの
• 境界が曲がっているもの（xorとかでは表せないもの）
  などがあるので、それをできるようにしようということで、
  進化系の方法がパーセプトロン以降出てきたというのがこれまでの歴史の流れになります。

おまけ

図形はこんな感じでかけます
多重パーセプトロンの図

import matplotlib.pyplot as plt

# plt.plot(x3)

plt.plot(3,100,marker='o')
plt.plot(70,40,marker='x')
plt.plot(92,98,marker='x')
plt.plot(6,92,marker='o')
plt.plot(97,70,marker='o')