はじめに
機械学習を扱っているので当然「勾配降下と共に損失を最小化する」という理論は知っていたのですが,意外と深掘ってみるとこれはぜひ整理に値するなと感じたので,Qiita に勾配降下についてまとめることにしました.
ちなみにタイトルの話に関しては本当に迷惑 (?) をしていて,私の場合言い間違える確率がベースライン 50% とほぼ同じです.勾配降下は英語で Gradient Descent なので GD であり,確率によって決定する特殊な場合に Stochastic という修飾語が付属するから "S"GD となるのです.
ちなみに SDGs とは持続可能な社会を作るために国連が設定した 17 個のゴールのことです.SDGs = Sustainable Development Goals なので,最後に G がついてる方はゴールの方だから我々には関係ないと思いましょう.
記事構成
最小二乗法
一言で表現するなら 「予測値 (モデルの出力)」と「真の値 (正解)」の二乗誤差を最小化する手法のこと である.数式で表現するなら $
||A\vec x - \vec b || $ の最小化である.大学の実験科目とかでグラフを描画するときに関数電卓でよく計算していた覚えがある.懐かしい.
線形モデルの場合
データが線形であろうと仮定が既にある場合をまず考える.
ただ,こんな場合は機械学習には存在しない,なぜならばあまりに単純なので機械学習でコストをかけて学習して予測する必要がないからである.(と言っておくと「機械学習の理論を知らずに当てはめバンバンで実験する」ことに対してアレルギーが発生する一部の研究者に支持をもらえるだろう.)
さて,入力データ $(x_0, x_1, x_2, x_3, ... x_n)$ に対して教師データ $(y_0, y_1, y_2, y_3, ... y_n)$ が用意されており,この関係が線形,つまり $y= a x + b$ であるという仮定を持っている時,判明していない変数は $a, b$ の 2 つとなる.この時,最小化したい値 L は次のように表現できる.
L = \sum_{i=0}^{n}(y_i-ax_i-b)^2
多変数モデルの場合
大体の機械学習ではこちらの概念を用いることが多いだろう.
入力データ $(x_0, x_1, x_2, x_3, ... x_n)$ に対して教師データ $(y_0, y_1, y_2, y_3, ... y_n)$ が用意されており,これを $k$ 次の多項式で表現されると仮定する.すると,同様に最小化するべき $L$ は次のように表現できる.
L = \sum_{i=0}^{n}(y_i - \sum_{j=0}^{k}a_j x^j)^2
外側は和算の意味のシグマ,内側は多項式の意味のシグマなのですが少々ややこしいということと,多項式から一般式への拡張性のため,関数 $f_w$ を用いて以下のように書き換えることにします.
また,損失関数の微分を考える際に係数が消えることから,$\frac{1}{2}$を掛けておくことも多いです.よって,以下の式のように示されます.
L = \frac{1}{2}\sum_{i=0}^{n}(y_i - f_{w}(x_i))^2
ちなみに,平均二乗誤差 (MSE: Mean Squared Error) はよく誤差関数の代表例として用いられるが,これはデータ全体に対する誤差の平均値である.数式で表現すると次のように表現できる.
L_{MSE} = \frac{1}{n} \sum_{i=0}^{n}(y_i - f_{w}(x_i))^2
また,MSE では各々の変数が二乗されているので,変数を 1 乗変数に戻して扱おう考えるアプローチ (変数自体の意味理解がしやすくなる?) も存在しており,これを 平方根平均二乗誤差 (RMSE: Root Mean Squared Error) と呼ぶ.
L_{RMSE} = \sqrt{ \frac{1}{n} \sum_{i=0}^{n}(y_i - f_{w}(x_i))^2}
最急降下法
一言で表現するなら 「アルゴリズムの目的は関数の底が知りたい,ある座標を見たときに微分値 (傾き) が正なら右肩上がりだから,左方に最小値がありそう,負なら右肩下がりだから右方に底がありそうだよね」 という手法.
この手法は数学者 Augustion-Louis Cauchy が提唱したとされており,当時からよくこんな現在まで使える技術を開発したなという感じですね.
英語版 wikipedia の記事 では,霧がある森の中,下山したい場合はとりあえず傾きに従って降りればいいじゃないかという話が書いてあって,少し気に入りました.
ちょっと文字だけだと何を言ってるか分からない可能性が高いので,今日は絵本を用意しました.
"数学的な説明の" 絵本
昔々あるところに二次関数のような関数がありました.

ある x 座標をランダムで取得し,グラフ上にぽつんと打ったそうな.すると,そこの位置で微分すると傾きが出てくるではありませんか.傾きが大きく右肩下がりだったので,大きく右に進むことに決めたそうな.

すると新たに x 座標が獲得できたので,その位置でもグラフを微分して傾きを出したそうな.右肩下がりではあったけれども,先程よりは傾きが大きくなかったのでさっきよりも控えめに右向きに進むことに決めたそうな.

するとびっくり,また新たに x 座標が獲得できたではありませんか.同じようにどんどん繰り返していきました.

同じようなことを何回も何回も繰り返すうち最終的にグラフの底にたどり着くことができたそうな,めでたしめでたし.
"機械学習的な説明の" 絵本 (といっても数学的な絵本の黒線が無い ver)
機械学習タスクにおいては,損失関数の定義 (= $L(y, \widehat{y})$) はされているが,その出力によってモデルによって生成される損失関数の概形 (= $L(w)$) は分かっていない.
そのため,学習初期段階ではランダムに生成された重み $w$ に基づいて導かれた損失関数の出力に対して微分をし,パラメータを探索する.
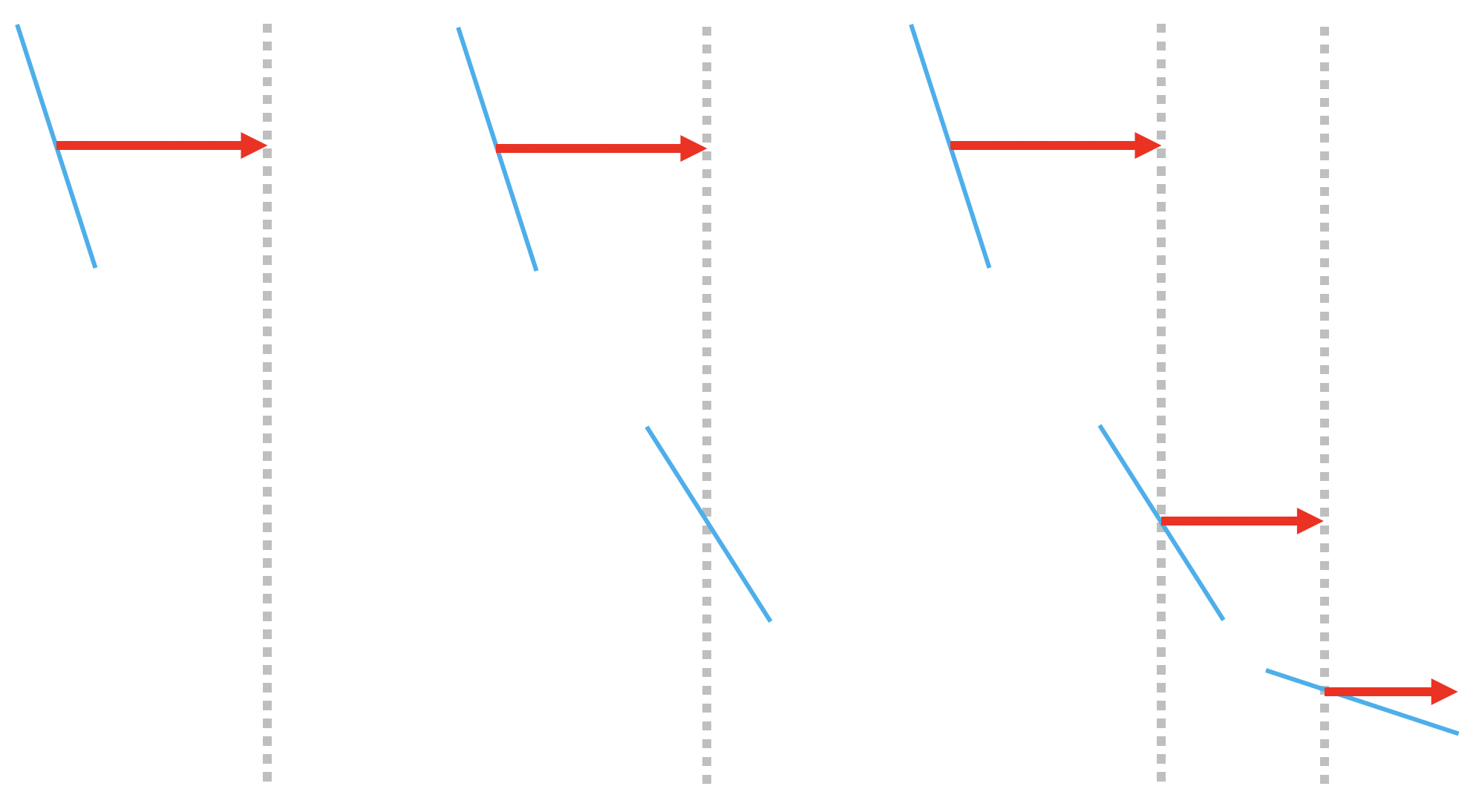
(左絵)
まずランダムに設定されたパラメータにおける結果を損失関数で評価する.そのときの勾配を計算して,この図の場合右肩下がりだったので右方に移動する.
(中絵)
移動した先でも同様に勾配を求めて...と繰り返す.
(右絵)
これらの操作を繰り返すことによって,この学習における損失関数の概形が見えてくることになる.繰り返すが 損失関数は実験前に定義されているが,実験の初期段階ではどの方向に進めば損失が最小化されるかは不明瞭なので,勾配に応じて移動することになる.
数式 - 準備編
絵本の内容では $y$ という目的関数 (損失関数) に対して,説明変数が $x$ の一つだけでした.そのため,説明としてはかなりざっくりとした説明になっています.
上記でも書きましたが,私が初学者のころ困惑した場所は,損失関数 $L$ において損失を決定する変数とは
- $y, \widehat{y}$ である
- $w$ である
の 2 種類の "考え方" が存在する点 にあった.
長い言い方に換えれば,
- 入力データ $x$ に対する真の正解 $y$ と出力 $\widehat{y}$ の差は損失関数によって決定されるので,$y, \widehat{y}$ こそが損失を決定する要因になるという考え方 (=損失関数上の点を求めたいという気持ち)
L(\widehat{y}, y)
- そもそも $\widehat{y}$ が決定されるのは機械学習過程によって決定される関数 (モデル) $f(x)$ なので,この関数もしくは変数 $w$ こそ損失を決定づける要因になるという考え方 (=損失関数の概形を求めたいという気持ち)
L(w) \mbox{または}
L(w( \widehat{y}, y))
となる.数式としてあまりに変数が乱雑に出てくるもので,この認識をあらためてしっかり持っておくことが必要だと私は感じています.
数式 - 立式編
まずはじめに,損失関数を整理します.今回は最小二乗法を用いることにします.(損失関数は最小二乗法だけではない点に注意!)
ここで $n$ とは学習データの数を示しており,$L$ は全ての学習データに対する損失関数の合計を示しています.
L = \frac{1}{2}\sum_{i=0}^{n}(y_i - f_{w}(x_i))^2
更新式は以下の通りになります.再度の記載になりますが,関数 $L$ における変数とはデータを示す $x, y$ ではなく $w$ である点に注意してください.
\begin{align}
w_{i+1} &:= w_{i} - l \frac{\partial L}{\partial w_i} \\
&:= w_{i} - l \frac{\partial \sum_{N}^{k=0}L_k}{\partial w_i} \\
\end{align}
言語で解説すると,ある重み $w_i$ における傾き $\frac{\partial L}{\partial w_i}$ が正であれば現在の座標 $x_i$ より負の方向に進む必要がある.また,最急降下法においては学習データ全ての誤差を計算するため,データ $N$ に対して全てのデータを足し合わせる.
ところで,この移動する "度合い" を決めるのが 式中の変数 $l$ で表現されている 学習率 (Learning rate) である. $l$ を小さくすると少しずつの変動になるし, $l$ を大きくすると Wild な変動になります.これを繰り返すことでグラフの底に辿り着くことができるというアルゴリズム.
問題点
ただし,このアルゴリズムは必ずしもグラフの底に到達できるとは限らず,局所解 (一見するとグラフの底だと思われる位置) に陥ってしまう.例えば,"4 次関数のような" 以下の関数例はどうだろう?

この場合,真のグラフの底は右方にあるのに左の解のような場所に囚われてしまっている.この場合,学習率の調整をするかもしくは最適化関数の工夫をしなければ最適解に辿り着くことはできない.
確率的勾配降下法 (SGD)
まず初めに記事を書くにあたって一言声を大にして言わせてください.
持続的社会だかなんだか知らんけど,SDGsとSGDがマジでややこしいからやめて!!!!!!!!!!!!!
おそらく全情報系の方の賛同を得られたと同時に全政治家に嫌われたところで,解説のほうに移りたいと思います.ちなみに SGD はシンガポールドルという意味もあるらしく,割と競合は多いらしい.
学習 (パラメータ更新) に用いるデータをランダムに獲得するかどうかという点で Stochastic (確率論的) なので,根底にあるのは GD (Gradient Descent) であるということを留意しておけば一応間違うことはないはずなのだが.
GD から SGD で変更された点
確率的勾配降下法 (SGD: Stochastic gradient descent) が最急降下法から変化させた点は以下の通りである.
- 目的:最急降下法の弱点である局所解に陥らないために
- 手段:あえて学習データを全て使用せずにランダムに選んだデータ 1 つを用いることで周辺も探索する
数式 - 立式編
先述の最急降下法では学習データ全てを使用したが,あえて偏りを持った勾配で計算することによって局所解に陥らないように解の周辺も探索する.更新式は以下の通り.
\begin{align}
w_{i+1} &:= w_{i} - l \frac{\partial L_k}{\partial w_i} \\
\end{align}
なお, $k$ はランダムに選んだデータのインデックス番号を示している.
最急降下法と確率的勾配降下法の比較
最急降下法のメリット
- データを一通り見ているので,最短距離で勾配を降下することができる.
- 解の良し悪しによらず最良と思しき解に素早く辿り着くことができる.
確率的勾配降下法のメリット
- データをランダムに取得しているので,メモリの消費が少ない.
- 重みの更新が最短とは限らないが,局所解に陥る可能性が低い.
参照させていただいたリンク集
Shogo Computing Laboratory 最急降下法
最適解の探索の挙動をアニメーションにされたものを描いていらっしゃって,これはすごくイメージがつきやすく分かりやすかったです.
DXCEL WAVE 【ディープラーニング】損失関数とパラメータ探索アルゴリズム徹底解説|勾配降下法・学習率・局所最適解と大域最適解問題
機械学習における損失関数の描写をどのように表現しようか迷っていたところ,ばっちりイメージ通りのものを描いていらっしゃいました.本当にわかりやすかったです.
物流業界の歩き方 勾配降下法で最小値が見つかる理由を数式と視覚でわかりやすく解
「グラフで点が転がり落ちる様子を視覚化する」という図が直感的な「最短距離」とは異なっていてかなり面白かったです.視覚化情報として勾配降下を見たい方は是非一度図を見に行ってみてください.
参照させていただいていないリンク集
United Nations Department of Economic and Social Affairs
Sustainable Development
持続可能社会を作るためのゴールとなる SDGs について国連が書いた記事です.ちなみに近年急速に耳にするようになってきたこの概念ですが,実は 2015年〜2030年 の目標として掲げられたものらしいので,実は 7 年目に突入しているのですね.