概要
宝くじは買わなければ当たらないが、買っても基本的に損するようになっている。
法律で払い戻し率50%以下と決まっている1ので、マクロにみると元を取るのは無理。
さらに言うと
その50%に満たない払い戻しの2/3ぐらいは高額当選に行くだろうから、
平時は15%でも戻ってくれば御の字かと思う。
(「何年かかけて2万投じて3000円戻ってきた」、というのが実感に近いのではなかろうか)
どんな数の組み合わせを選ぼうが、当選確率は変わらない。
一方、当選確率が変わらない中で、
人間の数選びの癖を使うと、当選金額を大きくできないか。
と考えた。
今回は分析のみ行う。
方針
当選番号は球を使った物理式の機械で弾き出している(脚注2リンク先の画像参照) ようなので、当選確率はこちらから介入できない。
しかし、当選金額は当選口数によってどうも山分け的な計算が行われるらしい。
(厳密には上限・下限額があるし、単純に山分けというわけでもないようだが)
つまり、こういうことになる。
- 他の人が選びやすい数 → 当選金額が目減り
- 他の人が選ばないような数→ 当選金額が大きい
人間はランダムに数を選ぼうと思った時に、
ランダムな数の組ではなくランダムそうな数の組を選ぶ癖があるはず。
さらに、ランダムそうでなくとも偏った数字を選ぶパターンはあるはず。
それをうまく利用してもし当たったときの金額を大きくできないか。
なぜロト6か
選べる数の範囲が1~43と広いため。(ミニロトは1~31 ロト7は1~37)
数の範囲が広いということは人間の癖が出やすいのでは?と予想
ただ、ロト6の方が当選等数が少なく、
日常的に買い続けた場合には非常に長い期間買い続けないと払い戻し額の平均値が安定しない気もする。
ロト7の方が、当選等数が多いので、当選金額が良い感じに均されて日常的には安定しそうな気もしている。
ただ、少額当選狙いはたとえ安定しても、
他人と被りやすそう(変に選び方にルールを付けた場合)、
払い戻し率が低い、
買うごとにむしり取られる三重苦
でもあるのでやめた方が良い。
環境
- Windows 10
- Python 3.7.1 (Anaconda3-2018.12-Windows-x86_64)
- +matplotlibの文字化け対処のためIPAexゴシックにフォント設定をしている
- 記載のコードは別途追加したモジュールへの依存はない…はず
過去結果の分析
元データは以下のサイトでcsv化済み(スクレイピングor転記?)データが公開されていたので、使わせていただいた。
http://kuji.vnox.net/loto6/20170614-3/
中身は以下のような内容。
取得時、第1263回までの結果が入っていた。(1年前なのでちょっと古い)
開催,抽選日,本数字1,本数字2,本数字3,本数字4,本数字5,本数字6,ボーナス数字,1等当選口数,1等当選金額,キャリーオーバー,2等当選口数,2等当選金額,3等当選口数,3等当選金額,4等当選口数,4等当選金額,5等当選口数,販売実績額
1263,2018-03-22,04,11,15,20,24,43,10,0,0,518679054,5,16225100,243,360500,12230,7500,205652,1638621800
1262,2018-03-19,09,20,26,29,30,34,42,0,0,248268877,3,24827700,143,562500,8652,9800,153917,1426903800
1261,2018-03-15,03,08,16,19,25,26,32,2,281942000,0,22,3613600,398,215700,18024,5000,259415,1734434200
...
これを読み込んで傾向を見ていく。
面倒なので今回ボーナス数字は見ない。
読み込み
以降の解析で必ず実行する部分。
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
df = pd.read_csv('loto6-csv\loto6.csv', encoding="sjis" )
nums_all = df[['本数字1','本数字2','本数字3','本数字4','本数字5','本数字6','ボーナス数字']]
plt.rcParams['figure.figsize'] = (8, 6)# 以降の図のデフォルトサイズ
plt.rcParams["font.size"] = 15
個数
本数字の個数は8841。(取得したcsv内の最新データが第1263回で、1263*7=8841となるのでデータ抜けは無さそうだ)
nums_all.values.flatten().size #=> 8841
平均値(全期間)
(nums_all.sum().sum())/(nums_all.size) #=> 22.130302002035968
平均値は1と43の算術平均である22。機械の出方に偏りはなさそう?
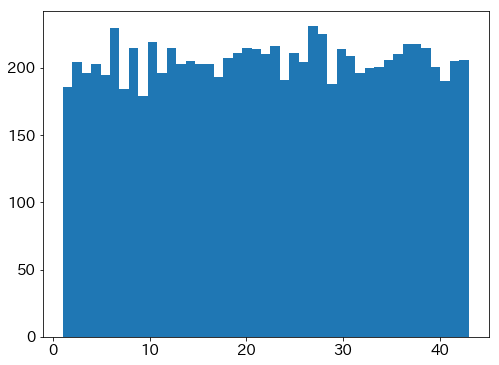
数の出現頻度(全期間)
plt.hist(nums_all.values.flatten(), bins=43)
plt.show()
結果を見ると、ヒストグラムはほぼ平らなのでやはり機械に偏りはなさそう。
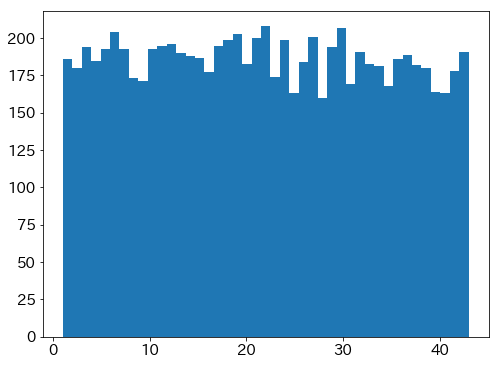
一様乱数との比較
なお、8000点の一様乱数でシードを変えてヒストグラム描いても似たような微妙な凸凹は出た。
シード変えて何回かやってみても同様だった。
# [1,43]の一様乱数を8000件生成
x = np.random.randint(1, 43+1, 8000 )
# ヒストグラムを出力
plt.hist(x, bins=43)
plt.show()
一様乱数(8000個)
機械の摩耗で数の出現確率が…と言っている怪しいサイトもあるようだが、特に関係ないと思う。
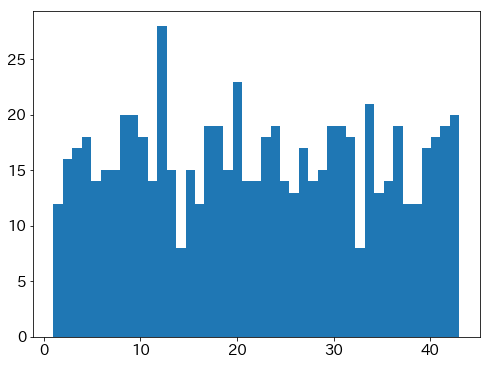
次に700個。
plt.hist(nums_all[0:100].values.flatten(), bins=43)
plt.show()
数の生成を8000個もやるとだいぶ均されていたが、700個にすると結構ばらつく。
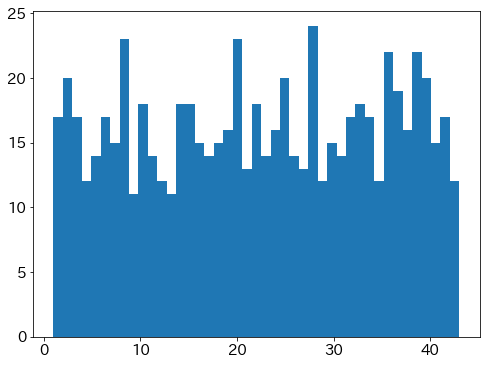
当選結果のデータからデータ内の最新100回も一応見てみる。
(2018年なので正確には最新ではないが)
700/7=100なのでロト6 100回相当。
一様乱数(700個)
実データ(700個, データ内の最新100回分)
短期間だと、こういったばらつきを見て右往左往する人も居そうだ。
ヒストグラムの結果より
当選数字に出現する数に目立つ偏りはなさそう。
これは予想通り。
回数が増えるとヒストグラムが平らになるので、
「数の出方が均等になるよう力が働く」みたいな思い込みをしている人も居そう。
(そういうことを言っている怪しいサイトもあった)
あるばらついたパターンがあったとして、
10倍の試行回数を経れば
そのパターンの他にも9種類の様々にばらついた頻度分布ができるので、
足し合わせれば均されて平らに近づくというだけの話だと思う。
とはいえ、
そういう思い込みがデータ上の傾向から見つかるか分析してみるのも面白そうではある。
時系列
青は生データ、オレンジは20回の移動平均。
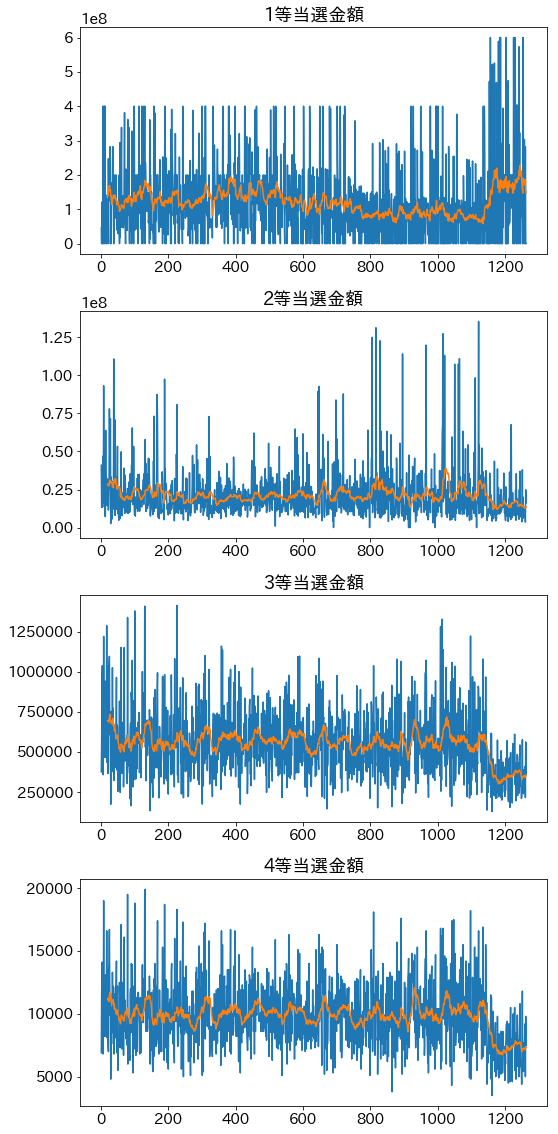
当選金額
コード(クリックで展開)
# 当選金額時系列
fig = plt.figure(figsize=(8.0, 16.0))
for rank in range(1,4+1):
rank_label = '{}等当選金額'.format(rank)
plt.subplot(4,1,rank)
plt.title(rank_label)
plt.plot( df['開催'], df[rank_label] )
# 新しい方が前になってるデータなので移動平均は逆順
plt.plot( df['開催'], (df[rank_label][::-1].rolling(20).mean())[::-1] )
plt.tight_layout()
plt.show()
- 開催750回あたりで1等の当選金額が一旦下がる変更があった?
- 開催1150回あたりで1等の最大値が増加し、2等以下は当選金額が減少
- 1等への比重を大きくする変更が行われた?
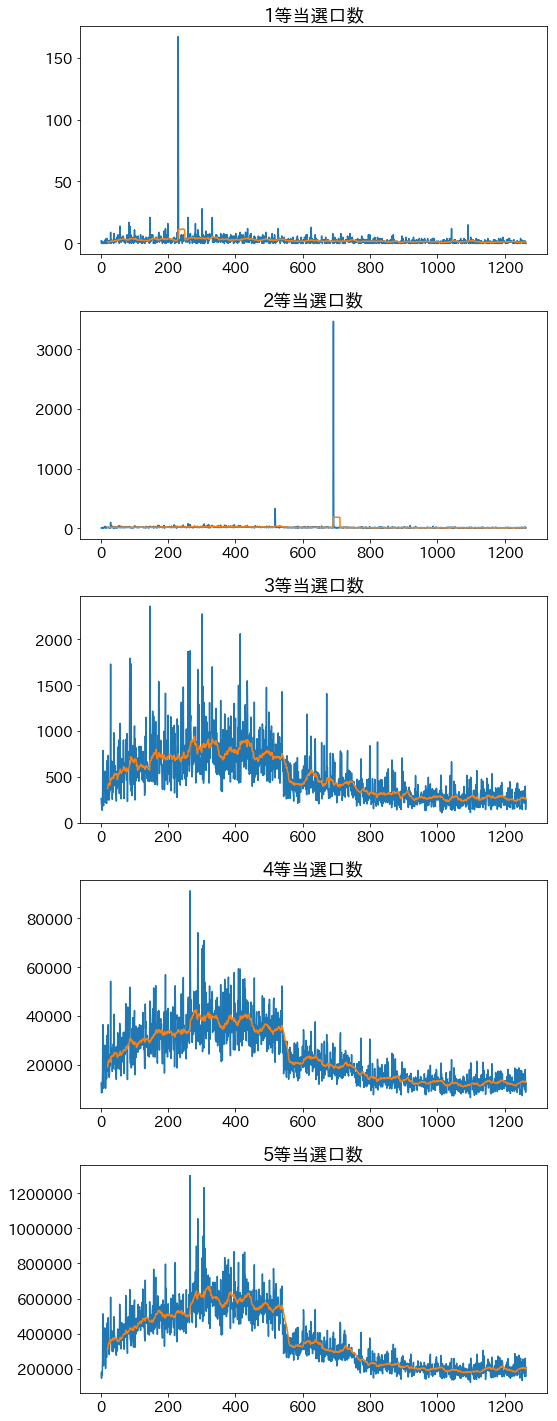
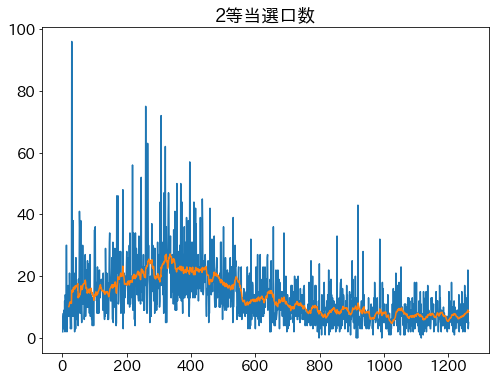
当選口数
コード(クリックで展開)
# 当選口数時系列
fig = plt.figure(figsize=(8.0, 20.0))
for rank in range(1,5+1):
rank_label = '{}等当選口数'.format(rank)
plt.subplot(5,1,rank)
plt.title(rank_label)
plt.plot( df['開催'], df[rank_label] )
# 新しい方が前になってるデータなので移動平均は逆順
plt.plot( df['開催'], (df[rank_label][::-1].rolling(20).mean())[::-1] )
plt.tight_layout()
plt.show()
1等、2等には当選口数が大きく増加する外れ値があり、グラフの傾向が読み取れない。
当選口数の外れ値と外れ値除去後のグラフ
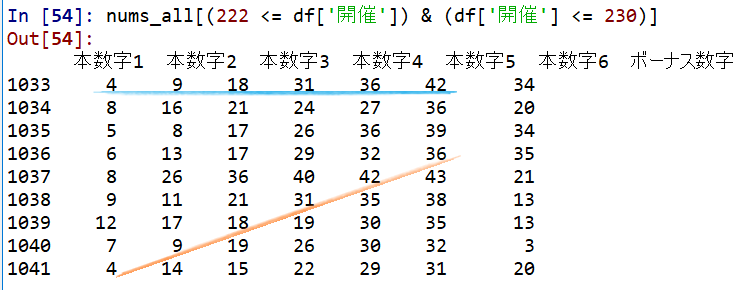
1等の当選数字の外れ値
調べると、第230回に167口の当選を出し、当選金額のワーストを記録したようだ。
過去に出た数の斜め買いをした人たち同士で重複したのが原因とのこと…
使用データ上でも一応見てみると、確かにそうなっていた。
選び方の偏りが実に人間らしい。
2等の当選口数の外れ値
最大の外れ値
- テレビドラマ「LOST」に出てくる数「4 8 15 16 23 42」による大量当選事件(第691回)の影響
- 作品に思い入れのある人たちがずっと同じ組み合わせで買っていたそうな
- 3470口当選して3等以下の当選金額になってしまったらしい
一応、csvにあるか確認。
nums_all[df['開催']==691]
本数字1 本数字2 本数字3 本数字4 本数字5 本数字6 ボーナス数字
4 7 8 15 16 42 23
2番目の外れ値
- 第518回もそこそこ大きな外れ値だが、なぜなのかは謎。
- 330口当選
- 怪しいサイトが煽った組み合わせだったとかだろうか?
nums_all[df['開催']==518]
本数字1 本数字2 本数字3 本数字4 本数字5 本数字6 ボーナス数字
14 31 34 35 40 42 25
外れ値除去後のグラフ
コード(クリックで展開)
idx_ignore = (df['開催']!=230)
rank_label = '1等当選口数'.format(rank)
plt.title(rank_label)
plt.plot( df[idx_ignore]['開催'], df[idx_ignore][rank_label] )
# 新しい方が前になってるデータなので移動平均は逆順
plt.plot( df[idx_ignore]['開催'], (df[idx_ignore][rank_label][::-1].rolling(20).mean())[::-1] )
plt.show()
idx_ignore = (df['開催']!=691) & (df['開催']!=518)
rank_label = '2等当選口数'.format(rank)
plt.title(rank_label)
plt.plot( df[idx_ignore]['開催'], df[idx_ignore][rank_label] )
# 新しい方が前になってるデータなので移動平均は逆順
plt.plot( df[idx_ignore]['開催'], (df[idx_ignore][rank_label][::-1].rolling(20).mean())[::-1] )
plt.show()
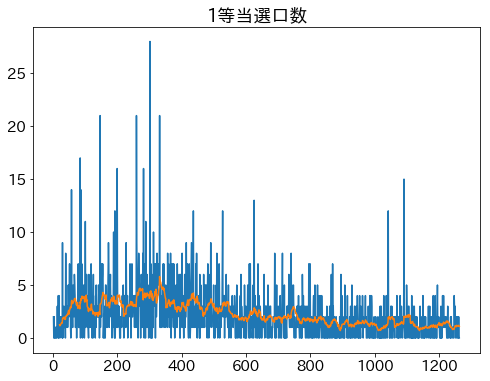
外れ値除去した場合の1等当選口数
外れ値除去した場合の2等当選口数
極端な外れ値を除去したことで時間的傾向は見えてきたが、
まだまだ1,2等両方で当選口数がぶっ飛んだ回がたびたび発生していることがわかる。
これも人間の選び方が偏っているからだろう。
個別の外れ値ケースを分析していると手間が多すぎるので、外れ値の分析は一旦ここまで。
まだ見ていない外れ値の方が人間の傾向を表した本質が詰まっているかもしれないので、
時間があれば記事を書くかもしれない。
その他
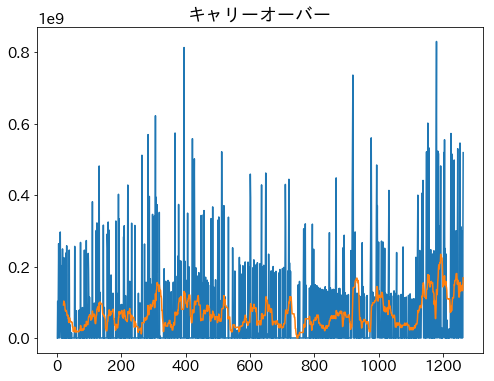
# キャリーオーバー・販売実績額 時系列
plt.title('キャリーオーバー')
plt.plot( df['開催'], df['キャリーオーバー'] )
plt.plot( df['開催'], (df['キャリーオーバー'][::-1].rolling(20).mean())[::-1] )
plt.show()
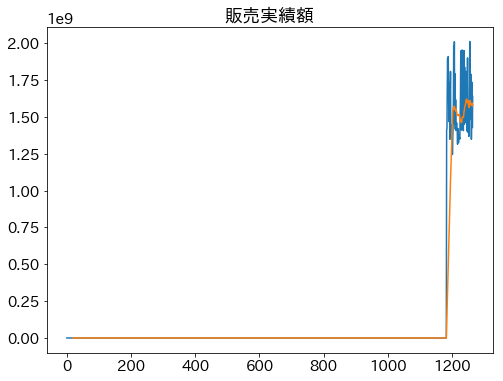
plt.title('販売実績額')
plt.plot( df['開催'], df['販売実績額'] )
plt.plot( df['開催'], (df['販売実績額'][::-1].rolling(20).mean())[::-1] )
plt.show()
- 開催1150回あたりでキャリーオーバーに段差のようなものが見える
- 1等への比重変更が行われた結果によるものか?
- 販売実績額は直近しかデータがなく、特にわかる情報は無し
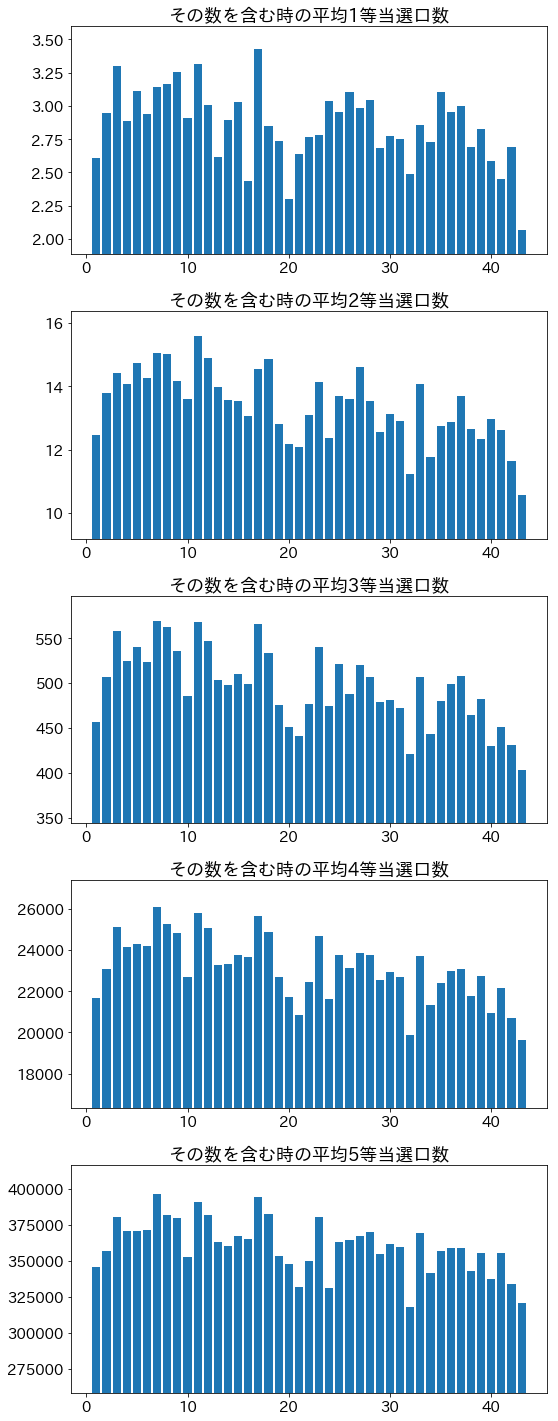
数ごとの当選金額・当選口数など(全期間)
人間が数を選ぶ以上、選ばれる数には偏りがあるはず。
その数が当選番号に含まれている、1等から4等までの当選金額・当選口数の平均を求める。
5等は金額固定なので見ない。
前述(当選口数の外れ値について)の極端な外れ値はデータへの影響が大きいので以降の解析では除去する。
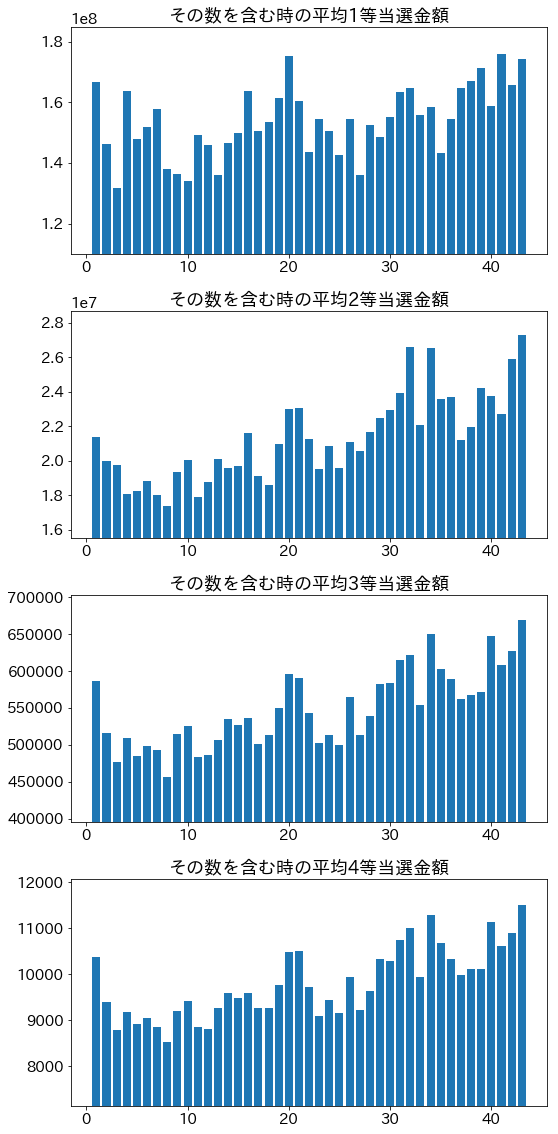
当選金額
当選金額は、当選なしの場合はデータ上0となっているので、それによって平均値が乱される恐れがある。
そのため、データに混入しないようにしている。
見やすいよう縦軸を0起点から変えているので注意すること。
コード(クリックで展開)
fig = plt.figure(figsize=(8.0, 16.0))
for rank in range(1,4+1):
rank_label = '{}等当選金額'.format(rank)
plt.subplot(4,1,rank)
average = np.zeros(43)
df_filt = df[df[rank_label] != 0]
if 1 == rank:
df_filt = df_filt[df_filt['開催']!=230]
elif 2 == rank:
df_filt = df_filt[(df_filt['開催']!=691) & (df_filt['開催']!=518)]
for n in range(1,43+1):
num_idx = (df_filt['本数字1'] == n) \
| (df_filt['本数字2'] == n) \
| (df_filt['本数字3'] == n) \
| (df_filt['本数字4'] == n) \
| (df_filt['本数字5'] == n) \
| (df_filt['本数字6'] == n)
if 2 == rank:
num_idx |= (df_filt['ボーナス数字'] == n)
data = df_filt[num_idx][rank_label]
average[n-1] = data.sum() / data.size
plt.title("その数を含む時の平均"+rank_label)
plt.bar(range(1,43+1), average, align="center")
plt.ylim([ (average.min() + average.max() / 2) / 2, None ])
plt.tight_layout()
plt.show()
当選口数
こちらも当選なしの場合は弾いている。
金額固定の5等も当選口数のデータはあるので5等まで見ておく。
コード(クリックで展開)
fig = plt.figure(figsize=(8.0, 20.0))
for rank in range(1,5+1):
rank_label = '{}等当選口数'.format(rank)
plt.subplot(5,1,rank)
average = np.zeros(43)
df_filt = df[df[rank_label] != 0]
if 1 == rank:
df_filt = df_filt[df_filt['開催']!=230]
elif 2 == rank:
df_filt = df_filt[(df_filt['開催']!=691) & (df_filt['開催']!=518)]
for n in range(1,43+1):
num_idx = (df_filt['本数字1'] == n) \
| (df_filt['本数字2'] == n) \
| (df_filt['本数字3'] == n) \
| (df_filt['本数字4'] == n) \
| (df_filt['本数字5'] == n) \
| (df_filt['本数字6'] == n)
if 2 == rank:
num_idx |= (df_filt['ボーナス数字'] == n)
data = df_filt[num_idx][rank_label]
average[n-1] = data.sum() / data.size
plt.title("その数を含む時の平均"+rank_label)
plt.bar(range(1,43+1), average, align="center")
plt.ylim([ (average.min() + average.max() / 2) / 2, None ])
plt.tight_layout()
plt.show()
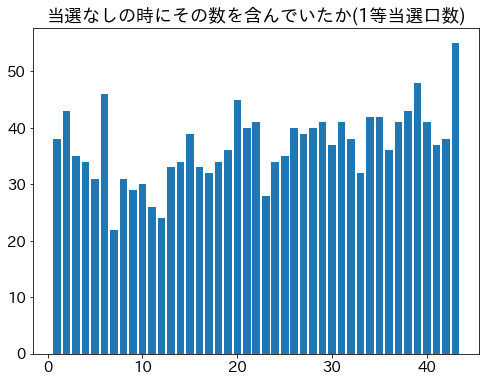
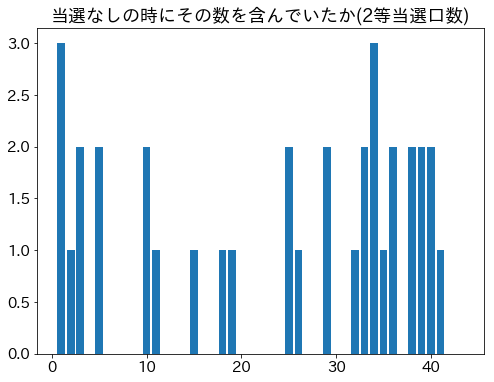
当選なしの時の数
コード(クリックで展開)
for rank in range(1,5+1):
rank_label = '{}等当選口数'.format(rank)
hist = np.zeros(43)
df_filt = df[df[rank_label] == 0]
for n in range(1,43+1):
num_idx = (df_filt['本数字1'] == n) \
| (df_filt['本数字2'] == n) \
| (df_filt['本数字3'] == n) \
| (df_filt['本数字4'] == n) \
| (df_filt['本数字5'] == n) \
| (df_filt['本数字6'] == n)
if 2 == rank:
num_idx |= (df_filt['ボーナス数字'] == n)
hist[n-1] += df_filt[num_idx][rank_label].size
plt.title("当選なしの時にその数を含んでいたか("+rank_label+")")
plt.bar(range(1,43+1), hist, align="center")
plt.show()
# 当選なしの時のヒストグラムを求めた場合でも意味的に同じグラフが描ける
# =============================================================================
# for rank in range(1,4+1):
# rank_label = '{}等当選口数'.format(rank)
# plt.hist(nums_all[df[rank_label] == 0].values.flatten(), bins=43, align="left")
# plt.show()
# =============================================================================
3等以下は当選なしの回はなし
読み取れる特徴
グラフ端の数 1または43を含むと当選金額大
- ⇔逆に当選口数は小さい
- 中間付近の数の方がランダムっぽいという思い込みが影響?
- 端の数は選ばれにくい
大きな数を含むほど当選金額大
- ⇔逆に当選口数は小さい
- 10以下の数はパッと直感とかで選ぶ人が多いのでは?
- 月日、誕生日や記念日などで選んでいる人がいる?(31以下は選ばれやすい)
- 小さな数は用途が広いので、選ばれやすい?
21,32を含むと当選口数が小さい
- 21は当選金額多くはない
- 32は当選金額多い
- 選ばれにくい理由はマークシート斜め選びの影響?
- マークシート上で21,32,43は斜めに並んでいて、上端に近い
- もしもこの方法が流行っている場合、端に近い組は選ばれにくそう
| 1 | 11 | 21 | 31 | 41 |
| 2 | 12 | 22 | 32 | 42 |
| 3 | 13 | 23 | 33 | 43 |
対策
今回は全期間の分析だけ。
これらの結果をもとに当選金額を大きくする方法を考えたい。
追記 or 続くか…?
-
ロト7(LOTO7)をもっと楽しむには?|宝くじ商品のご案内【宝くじ公式サイト】 "ロト専用抽せん機「電動攪拌式遠心力型抽せん機」" 2019-03-27アクセス ↩