2.5: 特徴量サンプリング

#概要

この記事では、Dr. Marcos著「Financial Machine Learning」の2章5節、特徴量サンプリングについて簡単な解説を行います。実際の応用として、特徴量サンプリングの手法の一つである、CUSUMフィルタを仮想通貨に対して適用した結果をご紹介します。

#特徴量サンプリングについて

2.3ではいくつかのバー(要はサンプリングの方法)について解説されています。2.5では、さらにサンプルデータの絞りこみについて解説が行われています。こちらを特徴量サンプリングと本では読んでいます。

#なぜ特徴量サンプリング？

では、なぜそもそも特徴量のサンプリングを行うのでしょうか？ナイーブに考えると、データの数が増えれば増えるほど、サンプルの数が増え、ロバストな学習が行えそうです。こちらは本にも記載されている通り、主に理由は二つあります。

1. モデルの学習のため
2. データ量削減により、精度が高まるため

です。1についでですが、いくつかのモデルは、多すぎるデータに大してはあまり機能しません(本の中ではSVMが挙げられています)。そもそもデータ数がすくない金融時系列データなのに、そんな状況があるのかというツッコミに対しては、例えば分足データや多資産のマルチインデックステーブルに対する予測をお考えください。
　2についてですが、こちらの方がより重要だと思われるのですが、適当にサンプルを選んだ方が精度は高まります。こちらを理解するためには、例えば、分かりやすくリーマンショックのような金融危機の例を考えてみてください。このような状況は、いわゆるアノマリー(分布のテール)に相当します。普段の市場と異なった状況になるわけです。このようなデータも含めて学習すると、例えば通常のマーケットでよく機能する特徴量から作られたモデルは、パフォーマンスにネガティブな影響があることが想定されます。そのため、そういったイベントを学習データから取り除くという施策に意味がある訳です。(ただ、オルタナティブデータなどから作られた特徴量で、そういったイベント下でも機能すると考えれられる特徴量であれば、訓練データに含めてパフォーマンスを見ることは意味があります。)

#CUSUMフィルタについて

では、そういったイベントはどのように検出すれば良いのでしょうか？そのための一例として、CUSUMフィルタが本では取り上げられています。ここで、以下の統計量を計算します:

\begin{align}
S_t &= max \{ 0, S_{t-1} + y_t - \mathbf{E}_{t-1}[y_t] \}
\end{align}

ここで、$y_t$は局所定常過程、$S_0=０$とします。局所(弱)定常過程なので、

\begin{align}
\mathbf{E}_{t-1}[y_t] &= const.
\end{align}

です。つまり、単なる定数で閾値を変えるだけなので、0と置いてしまいます。$y_t$は特徴量でも、ラベルでも、なんでも良いです。要は、$S_t$は測定した値が(それまでの経路で取った値も含めて)どれくらい平均的に離れているかを表しています。ここで、ある閾値$h$を設定して、$S_t>h$であれば、イベントであるとします。以下、負の方向のイベントも含めて(対称CUSUMフィルタ)、イベントをサンプリングするコードです。

def getTEvents(gRaw: pd.Series, h: float) -> pd.DatetimeIndex:
    
    # Initialization
    tEvents, sPros, sNeg = [], 0, 0
    
    diff = gRaw.diff()
    
    for i in diff.index[1:]:
        
        sPros, sNeg = max(0, sPros + diff.loc[i]), min(0, sNeg + diff.loc[i])
        
        if sNeg < -h:
            sNeg = 0
            tEvents.append(i)
        elif sPros > h:
            sPros = 0
            tEvents.append(i)
            
    return(pd.DatetimeIndex(tEvents))

ここで、以下のある仮想通貨の価格時系列に対して、上記のCUSUMフィルタを適用します。

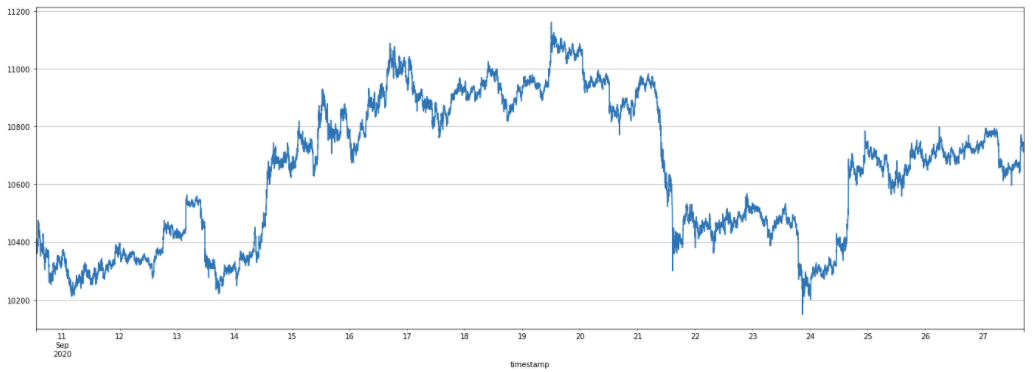
適当にパラメーター$h$を設定すると、以下のようなイベントがサンプリングされます。

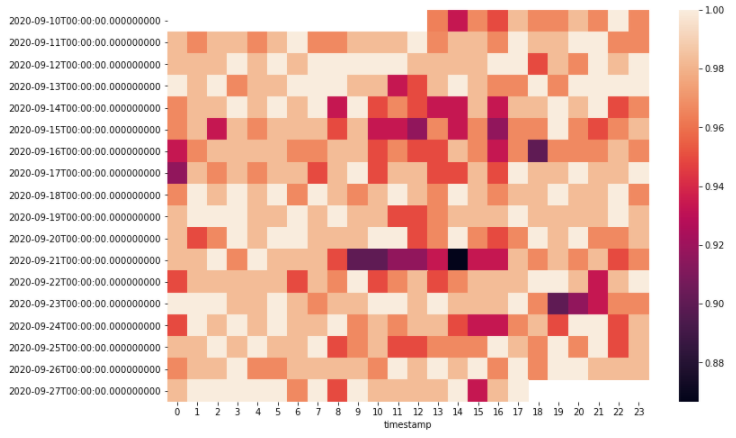
ここから、 実際のアルファリサーチにおいては、上記のイベントになんらかの共通性がみられるか？その共通性には、どういった定性的な背景があるかなど(例えば、雇用統計などファンダメンタルなイベントが起こっているのかなど)を詳しく調べていきます(ここが個人的にはリサーチで一番面白いところですね)。ここでは、例として日付・時間ごとのイベント数のヒートマップを描いてみます(以下のグラフでは、パラメータ$h$の値を下げています)。

こちらのヒートマップを見ると、10-15時くらいでは、イベントの数が多いようです。つまり、この時間帯ではリターンが(どちらか一方に)大きく動きやすいということになります。言い換えると、トレンドが効きやすいということです。したがって、モメンタム系の特徴量をモデルに与えるとすると、上記の時間帯でモデルを学習し、上記の時間帯のみで運用する方が、全ての時間帯で学習し運用するよりも、パフォーマンスが向上するのではないか？という仮説が立つわけです。また、逆にそれ以外の時間では回帰的な動きをしやすいため、回帰性を前提とする特徴量などをモデルに入れればより良いパフォーマンスが得られるのではないかという仮説が立ちます。

#まとめ

本記事では、特徴量サンプリングの一つであるCUSUMフィルタについて解説を行いました。特徴量サンプリングは、モデルのベストパフォーマンスを追求するために必要です。あと、こちらは本に記載されていない余談ですが、他の特徴量サンプリングの手法として、直近のラベルとの相関(情報係数)が逆転している訓練期間を除くといった手法等があります。