凸包を求めるアルゴリズム（ギフト包装法）

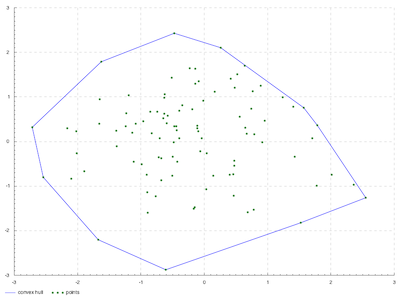
数学における凸包または凸包絡は、与えられた集合を含む最小の凸集合である。 Wikipedia: 凸包

上図のように点の集合が与えられた時にその凸包を求めるアルゴリズムを実装してみたのでメモとして残しておきます。

Linear Algebra

まずは計算に必要になる点やベクトルと言った概念を定義しておきます。

-- | ２次元の点
type Point = (Double, Double)

-- | ２次元ベクトル
type Vector = (Double, Double)

-- | ２点からベクトルを作成
to :: Point -> Point -> Vector
to (x0, y0) (x1, y1) = (x1 - x0, y1 - y0)

-- | ノルムを計算する
norm :: Vector -> Double
norm (x, y) = sqrt $ x ^ 2 + y ^ 2

-- | 単位ベクトルに変換する
normalize :: Vector -> Vector
normalize v@(x, y) = let r = norm v in (x / r, y / r)

-- | 直交ベクトルに変換する
orthogonalize :: Vector -> Vector
orthogonalize (x, y) = (-y, x)

-- | 内積を取る
dot :: Vector -> Vector -> Double
dot (x0, y0) (x1, y1) = x0 * x1 + y0 * y1

ギフト包装法

ギフト包装法やJarvisの行進法とは、計算幾何学における点の集合の凸包を求めるアルゴリズム。 Wikipedia: ギフト包装法

ギフト包装法は凸包を求める最良のアルゴリズムというわけではないようですが、仕組みがとてもわかり易かったので実装してみました。

簡単に説明すると

1. まず凸包の境界に含まれる１点を見つける
2. 選んだ1点から別の点に直線を結び他のすべての点がその直線の片側に来るような点を見つける
3. 2を1で選んだ点が再び選ばれるまで繰り返す

という感じです

import Data.List (sort, sortOn, (\\))

-- | 与えられたベクトルとその始点からの偏角を計算する
angle :: Point -> Vector -> Point -> Double
angle p0 v p1 =
  let nv = normalize v
      ov = orthogonalize nv
      v' = p0 `to` p1
   in atan2 (v' `dot` ov) (v' `dot` nv)

-- | ２次元の線
type Line = [Point]

-- | ギフト包装法で与えられた点群の凸法を求める
giftWrapping :: [Point] -> Line
giftWrapping ps | length ps < 3 = ps
giftWrapping ps =
  let p0 = head $ sort ps
      vx = (1.0, 0.0)
      p1 = head . sortOn (angle p0 vx) $ ps \\ [p0]
   in go [p1, p0] ps
  where
    go :: [Point] -> [Point] -> [Point]
    go history ps =
      let [p2, p1] = take 2 history
          v = p1 `to` p2
          pn' = head . sortOn (angle p2 v) $ ps \\ [p2, p1]
       in if pn' == last history
             then pn' : history
             else go (pn' : history) ps

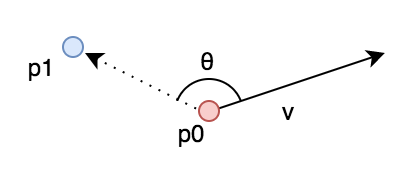
angle は与えられた点p0とベクトルvからそれを基準とした別の点p1の偏角を計算する関数です。図にすると以下のような θ を求めています。

動作確認

作ったギフト包装法のアルゴリズムを検証してみましょう。今回は mwc-random を使ってランダムな点を生成し、Chart と Chart-cairo を使って描画して画像に書き出しました。

import Graphics.Rendering.Chart.Easy (plot, line, points, def)
import Graphics.Rendering.Chart.Backend.Cairo (toFile)
import System.Random.MWC (withSystemRandom, asGenIO)
import System.Random.MWC.Distributions (normal)

-- | ランダムな２次元の点群を生成する
generatePoints :: Int -> IO [Point]
generatePoints n = do
  withSystemRandom . asGenIO $ \gen -> do
    xs <- sequence . replicate n $ normal 0 1 gen
    ys <- sequence . replicate n $ normal 0 1 gen
    pure $ zip xs ys

-- | 結果をプロットして画像に書き出す
saveImage :: FilePath -> [Point] -> Line -> IO ()
saveImage path ps ln = toFile def path $ do
  plot (line "convex hull" [ln])
  plot (points "points" ps)

main :: IO ()
main = do
  ps <- generatePoints 100
  let ln = giftWrapping ps
  saveImage "gift-wrapping.png" ps ln

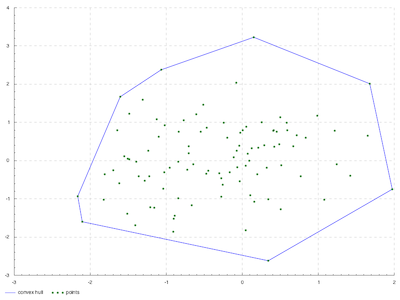
結果を見てみましょう

うまくいってそうですね

完全なプログラム

import Data.List (sort, sortOn, (\\))

import Graphics.Rendering.Chart.Easy (plot, line, points, def)
import Graphics.Rendering.Chart.Backend.Cairo (toFile)
import System.Random.MWC (withSystemRandom, asGenIO)
import System.Random.MWC.Distributions (normal)

--------------------
-- Linear Algebra
--------------------

-- | ２次元の点
type Point = (Double, Double)

-- | ２点からベクトルを作成する
to :: Point -> Point -> Vector
to (x0, y0) (x1, y1) = (x1 - x0, y1 - y0)

-- | ２次元ベクトル
type Vector = (Double, Double)

-- | ノルムを計算する
norm :: Vector -> Double
norm (x, y) = sqrt $ x ^ 2 + y ^ 2

-- | 単位ベクトルに変換する
normalize :: Vector -> Vector
normalize v@(x, y) = let r = norm v in (x / r, y / r)

-- | 直交ベクトルに変換する
orthogonalize :: Vector -> Vector
orthogonalize (x, y) = (-y, x)

-- | 内積を取る
dot :: Vector -> Vector -> Double
dot (x0, y0) (x1, y1) = x0 * x1 + y0 * y1

-----------------------------
-- Gift Wrapping Algorithm
-----------------------------

-- | 与えられたベクトルとその始点からの偏角を計算する
angle :: Point -> Vector -> Point -> Double
angle p0 v p1 =
  let nv = normalize v
      ov = orthogonalize nv
      v' = p0 `to` p1
   in atan2 (v' `dot` ov) (v' `dot` nv)

-- | ２次元の線
type Line = [Point]

-- | ギフト包装法で与えられた点群の凸法を求める
giftWrapping :: [Point] -> Line
giftWrapping ps | length ps < 3 = ps
giftWrapping ps =
  let p0 = head $ sort ps
      vx = (1.0, 0.0)
      p1 = head . sortOn (angle p0 vx) $ ps \\ [p0]
   in go [p1, p0] ps
  where
    go :: [Point] -> [Point] -> [Point]
    go history ps =
      let [p2, p1] = take 2 history
          v = p1 `to` p2
          pn' = head . sortOn (angle p2 v) $ ps \\ [p2, p1]
       in if pn' == last history
             then pn' : history
             else go (pn' : history) ps

-----------
-- Misc.
-----------

-- | ランダムな２次元の点群を生成する
generatePoints :: Int -> IO [Point]
generatePoints n = do
  withSystemRandom . asGenIO $ \gen -> do
    xs <- sequence . replicate n $ normal 0 1 gen
    ys <- sequence . replicate n $ normal 0 1 gen
    pure $ zip xs ys

-- | 結果をプロットして画像に書き出す
saveImage :: FilePath -> [Point] -> Line -> IO ()
saveImage path ps ln = toFile def path $ do
  plot (line "convex hull" [ln])
  plot (points "points" ps)

----------
-- Main
----------

main :: IO ()
main = do
  ps <- generatePoints 100
  let ln = giftWrapping ps
  saveImage "gift-wrapping.png" ps ln