このスライドはモナド勉強会 at Nakameguro.hs #2の発表資料です
Nakameguro.hs これまでの軌跡
今回ほぼ3年ぶりに開催！
平日にサクッと集まってHaskellのニッチな話題について語れる勉強会としてやっていきたい気持ちです
モナドに至る道
なぜモナドが重要なのか？
私たちは関数のみを使ってプログラミングしたい。(つまるところ「関数型プログラミング(FP)」)
なぜモナドが必要なのか？ - Qiita
しかし非決定的な計算・副作用を伴う計算などなど、関数でどう扱えばいい?
モナドは値およびその値を使う計算の並びという観点からいえば、計算を構造化する方法です
モナドのすべて - イントロダクション
非決定性・副作用・例外処理など全部モナドで構造化された計算として表してしまえばいい！
（そしてそれが可能である！）
それが良いかどうかは別として、純粋さをとことん追求した必然の孤高の帰結がモナドというわけです
モナドはなぜHaskellでしか積極的に使われていないのか? - uehaj's blog
最近はasync/await等よく似た機能が他の言語にも徐々に取り入れられている
増え続けるモナドチュートリアル
プログラミングにおけるモナドの起源
E. Moggi "Computational Lambda-Calculus and Monads" (1988)
プログラミングにおけるモナドの初期の歴史について - 再帰の反復blog
世の中にはたくさんのモナドチュートリアルが溢れている
それだけ注目されているが理解するのが簡単ではないということ
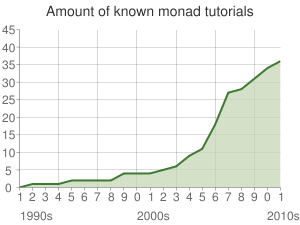
Monad tutorials timeline - HaskellWiki
今日はせっかくの勉強会なので対話を通して一人ひとりの理解に向き合えたらと思います
なので気軽にいつでも質問してください！
Haskellのおさらい
Haskell Recap / Hello World
あとに出てくるコードを読むために必要な知識を高速におさらい
main :: IO ()
main = putStrLn "Hello World"
mainに書かれた処理が実行されます
> :t putStrLn
putStrLn :: String -> IO ()
Haskell Recap / 型
型を定義する3つの方法
-- 型シノニム
-- 既存の型に別名をつける
type Point = (Int, Int)
-- newtype は既存の型と同値な型を定義する
newtype Reader r a = Reader { runReader :: r -> a }
-- data は全く新しい型を定義する
data Signal = Green | Yellow | Red
Haskell Recap / 関数
パターンマッチ
canGo :: Signal -> Bool
canGo Green = True
canGo _ = False
case式
canGo :: Signal -> Bool
canGo x = case x of
Green -> True
_ -> False
再帰
take :: Int -> [a] -> [a]
take 0 _ = []
take n (x:xs) = x : take (n-1) xs
中置記法
> :t elem
elem :: a -> [a] -> Bool
> 5 `elem` [1..10]
True
Haskell Recap / 高階型
型を受け取って型になる型
data Maybe a = Nothing | Just a
data [] a = [] | a : [a]
2つ以上の型変数も扱える
data (,) a b = (,) a b
data (->) a b = ...
受け取った方の値を使わない幽霊型
data Const a b = Const a
Haskell Recap / 高階関数
関数を引数に取ったり、関数を返り値にしたりする型
map :: (a -> b) -> ([a] -> [b])
合成関数の演算子
(.) :: (b -> c) -> (a -> b) -> (a -> c)
Haskell Recap / リスト操作
> [1,2,3,4,5]
[1,2,3,4,5]
> -- レンジ
> [1..5]
[1,2,3,4,5]
> -- 無限リスト
> repeat 1
[1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,^C
> -- リストの長さ
> length [1..5]
5
> -- map :: (a -> b) -> [a] -> [b]
> map (*2) [1..5]
[2,4,6,8,10]
> -- zip :: [a] -> [b] -> [(a, b)]
> zip [1..5] ['a'..'z']
[(1,'a'),(2,'b'),(3,'c'),(4,'d'),(5,'e')]
> -- zipWith :: (a -> b -> c) -> [a] -> [b] -> [c]
> zipWith (+) [1..5] [100..]
[101,103,105,107,109]
> -- concat :: [[a]] -> [a]
> concat [[1, 2], [3, 4], [5, 6]]
[1,2,3,4,5,6]
> -- concatMap :: (a -> [b]) -> [a] -> [b]
> concatMap (\x -> [x, 10 * x]) [1..5]
[1,10,2,20,3,30,4,40,5,50]
モナドのエッセンスがここに詰まっています
まずは型クラス
型クラス
"アドホック多相"を実現するための言語機能
class Show a where
show :: a -> String
showは型クラスShowのインスタンスになっている型なら何でも引数に取れる
> show 123
"123"
> show True
"True"
> -- これはダメな例
> show length
• No instance for (Show ([a0] -> Int)) arising from a use of ‘show’
...
インスタンスの定義
data Signal = Green | Yellow | Red
instance Show Signal where
show Green = "Green"
show Yellow = "Yellow"
show Red = "Red"
> show Green
"Green"
関数の型には型クラス制約として現れる
> :t print
print :: Show a => a -> IO ()
> print 123
123
> print True
True
> print "Haskell"
"Haskell"
> print Red
Red
代表的な型クラス / Eq
値が同じかどうか比較するための型クラス
class Eq a where
(==) :: a -> a -> Bool
(/=) :: a -> a -> Bool
x == y = not (x /= y)
x /= y = not (x == y)
インスタンスの例
instance Eq Bool where
True == True = True
False == False = True
_ == _ = False
instance (Eq a, Eq b) => Eq (a, b) where
(x1, y1) == (x2, y2) = x1 == x2 && y1 == y2
代表的な型クラス / Ord
値の大小を比較するための型クラス
data Ordering = LT | EQ | GT
class Eq a => Ord a where
compare :: a -> a -> Ordering
(<), (<=), (>), (>=) :: a -> a -> Bool
max, min :: a -> a -> a
compare x y = if x == y then EQ
else if x <= y then LT
else GT
x < y = case compare x y of { LT -> True; _ -> False }
x <= y = case compare x y of { GT -> False; _ -> True }
x > y = case compare x y of { GT -> True; _ -> False }
x >= y = case compare x y of { LT -> False; _ -> True }
max x y = if x <= y then y else x
min x y = if x <= y then x else y
インスタンスの例
instance Ord Bool where
True <= True = True
False <= True = True
True <= False = False
False <= False = True
代表的な型クラス / 数値型
Num
整数のような計算（足し算掛け算等）を備えた型クラス
class Num a where
(+) :: a -> a -> a
(-) :: a -> a -> a
(*) :: a -> a -> a
negate :: a -> a
abs :: a -> a
signum :: a -> a
fromInteger :: Integer -> a
x - y = x + negate y
negate x = 0 - x
インスタンスの例
instance Num Int where
...
instance Num Double where
...
Fractional
割り算が出来るような演算を備えた型クラス
class Num a => Fractional a where
(/) :: a -> a -> a
recip :: a -> a
fromRational :: Rational -> a
recip x = 1 / x
x / y = x * recip y
インスタンスの例
instance Fractional Double where
...
Haskellの数値系型クラスの関係
[Numeric Tower - WHAT I WISH I KNEW WHEN LEARNING HASKELL](http://dev.stephendiehl.com/hask/#numeric-tower)
代表的な型クラス / Monoid
結合演算とそれに対する単位元を備えた型クラス
class Monoid a where
mempty :: a
mappend :: a -> a -> a
mconcat :: [a] -> a
mconcat = foldr mappend mempty
インスタンスの例
instance Mononid [a] where
mempty = []
mappend xs ys = xs ++ ys
-- 足し算に関するモノイド
newtype Sum a = Sum { getSum :: a }
instance Num a => Monoid (Sum a) where
mempty = Sum (fromIntegral 0)
mappend (Sum x) (Sum y) = Sum (x + y)
-- 掛け算に関するモノイド
newtype Product a = Product { getProduct :: a }
instance Num a => Monoid (Product a) where
mempty = Product (fromIntegral 1)
mappend (Product x) (Product y) = Product (x * y)
Functor Applicative Monad
型クラスの依存関係
[The Typeclassopediaを訳しました, The Typeclassopedia - #3(2009-10-20)](http://snak.tdiary.net/20091020.html)
Functor
Functor
class Functor f where
fmap :: (a -> b) -> f a -> f b
普通の関数をFunctorに包まれた型に適用できるようにするのがfmap
日本語で関手とも呼ばれる
Functor / Maybe
data Maybe a = Nothing | Just a
instance Functor Maybe where
fmap f Nothing = Nothing
fmap f (Just a) = Just (f a)
Maybeのfmapは中身があれば作用する
> fmap (+1) Nothing
Nothing
> fmap (+1) (Just 1)
Just 2
> fmap (++" World") (Just "Hello")
Just "Hello World"
Functor / List
data [] a = [] | a : [a]
instance Functor [] where
fmap f [] = []
fmap f (x:xs) = f x : fmap f xs
リストのfmapは全ての中身に作用する
> [1..5]
[1,2,3,4,5]
> fmap (+1) [1..5]
[2,3,4,5,6]
> fmap (+1) []
[]
Functor / ZipList
ZipListは型としてリストと同型
> :i ZipList
newtype ZipList a = ZipList {getZipList :: [a]}
Functorの実装はリストと同じ
instance Functor ZipList where
fmap f (ZipList xs) = ZipList (fmap f xs)
後に出てくるApplicativeの実装に違いが出てくる
Functor / 関数
instance Functor ((->) r) where
-- fmap :: (a -> b) -> (r -> a) -> (r -> b)
fmap f g = f . g
関数のfmapは関数合成
> fmap (+1) (+2) 3
6
> fmap (++ "sec") show 5
"5sec"
Functor / Const
data Const a b = Const a
instance Functor (Const a) where
fmap f (Const a) = Const a
Constのfmapは"何もしない"
> fmap (++ "Hello") (Const 1)
Const 1
Applicative
Applicative
class Functor f => Applicative f where
pure :: a -> f a
(<*>) :: f (a -> b) -> f a -> f b
pureを使って値を包むことが出来る(Pointed)
(<*>)を使って包まれた世界の中で関数適用をすることが出来る
Applicative / Maybe
instance Applicative Maybe where
pure = Just
Nothing <*> _ = Nothing
_ <*> Nothing = Nothing
(Just f) <*> (Just a) = Just (f a)
Maybeのpureは値をJustで包む
Maybeの<*>は中身があれば作用させる
> Just (+1) <*> Just 2
Just 3
Applicative / List
instance Applicative [] where
pure a = [a]
fs <*> xs = concat (map (\f -> map (\x -> f x) xs) fs)
-- [f x | f <- fs, x <- xs]
リストのpureは一つの要素を持つリストを作る
リストの<*>は全ての組み合わせで作用させる
> [(+1), (*2)] <*> [1, 2]
[2,3,2,4]
Applicative / ZipList
instance Applicative ZipList where
pure a = ZipList (repeat a)
(ZipList fs) <*> (ZipList xs) = ZipList (zipWith (\f x -> f x) fs xs)
-- ZipList (zipWith ($) fs xs)
ZipListのpureは値を無限にコピーする
ZipListの<*>はリストの中身を対応する順番に作用させる
> ZipList [(+1), (*2)] <*> ZipList [1, 2]
ZipList {getZipList = [2,4]}
> ZipList [(+1), (*2)] <*> ZipList [1]
ZipList {getZipList = [2]}
Applicative / 関数
instance Applicative ((->) r) where
pure a = const a
f <*> g = \r -> f r (g r)
関数のpureは定数関数を作る
関数の<*>は全ての関数に引数を作用させる
> pure 1 "Hello"
1
> ((+) <*> (+1)) 1
3
Applicative / Const
Const aはApplicativeのインスタンスには出来ない
ただしaがMonoidであれば可能
instance Monoid a => Applicative (Const a) where
pure _ = mempty
(Const a) <*> (Const b) = Const (a `mappend` b)
Monad
Monad
class Applicative m => Monad m where
(>>=) :: m a -> (a -> m b) -> m b
(>>=) は包まれた値を、値を変換して包まれた値にする関数に適用して包まれた値を作成する
実はこれはdo構文に適した定義になっている
同値でより分かりやすそうなモナドの定義を後で紹介します
Monad / Maybe
Maybeは失敗するかもしれない計算を構造化するモナド
instance Monad Maybe where
Nothing >>= _ = Nothing
(Just a) >>= k = k a
> :t find
find :: (a -> Bool) -> [a] -> Maybe a
> :t lookup
lookup :: Eq a => a -> [(a, b)] -> Maybe b
> Just 3 >>= (\x -> find (\n -> n `mod` x == 0) [10..15] >>= (\y -> lookup y [(12, "A"), (15, "B")]))
Just "A"
>>= を使った書き方はすぐに煩雑になってしまう
do記法
do構文を使えばあたかも逐次的な処理を記述しているかのように書ける
Just 3 >>= (\x -> find (\n -> n `mod` x == 0) [10..15] >>= (\y -> lookup y [(12, "A"), (15, "B")]))
== -- ここはただ整形してるだけ
Just 3 >>= (\x ->
find (\n -> n `mod` x == 0) [10..15] >>= (\y ->
lookup y [(12, "A"), (15, "B")]))
== -- do構文！
do
x <- Just 3
y <- find (\n -> n `mod` x == 0) [10..15]
lookup y [(12, "A"), (15, "B")]
Maybeはどこかの計算で失敗すれば全体が失敗する
Monad / List
リストは非決定的な計算を構造化するモナド
instance Monad [] where
xs >>= k = concat (fmap k xs)
-- concatMap k xs
これはいわゆるflatMap
> do
| x <- [1..30]
| y <- [x..30]
| z <- [y..30]
| if x^2 + y^2 == z^2 then [(x,y,z)] else []
[(3,4,5),(5,12,13),(6,8,10),(7,24,25),(8,15,17),(9,12,15),(10,24,26),(12,16,20),(15,20,25),(18,24,30),(20,21,29)]
上記のようにモナドを使えば"前の値"に応じて計算を分岐することが出来る
構造化定理 (...) 逐次、反復、分岐があれば、計算しうる計算はすべて記述できるという定理です。Monad の説明にありがちな圏論を持ち出されるより、よっぽどいいでしょう？
Haskell の Monad とは言語内DSLのフレームワークである - あどけない話
Monad / ZipList
ZipListはモナド則を満たせないのでモナドにはなりません（後述）
Monad / 関数
関数はある引数を受け取る計算を構造化するモナド
instance Monad ((->) r) where
f >>= k = \r -> k (f r) r
> average = do
| x <- sum
| y <- length
| pure (x / fromIntegral y)
> average [1..10]
5.5
このモナドはReaderとも呼ばれ便利に使われます（詳しくは後半のセッションで）
考えているモナドによってdo構文が直感的に表している手続き的な操作の意味がそれぞれ変わってくる
この感覚を以ってモナドは文脈とも言われている
もっとモナドの例 / IO
IOはOSとやり取りするためのEDSL
"Building Haskell Programs with Fused Effects" by Patrick Thomson - YouTube
> :t getLine
getLine :: IO String
> :t putStrLn
putStrLn :: String -> IO ()
IOはモナドなのでdo構文を使って組み合わせることが出来る
> :{
| do
| putStrLn "お名前は？"
| name <- getLine
| putStrLn ("こんにちは" ++ name)
| :}
お名前は？
lotz
こんにちはlotz
もっとモナドの例 / Hedis
HaskellのRedisクライアント
> :t set
set :: String -- key
-> String -- value
-> Redis Status
> :t get
get :: String -- key
-> Redis (Maybe String)
> :t runRedis
runRedis :: Connection -> Redis a -> IO a
Redisはモナドなのでdo構文を使って組み合わせることが出来る
> runRedis conn $ do
| set "hello" "hello"
| set "world" "world"
| hello <- get "hello"
| world <- get "world"
| pure (hello, world)
(Just "hello", Just "world")
※分かりやすさを優先して少し型は変えてます
モナドに至る別の道
joinで実装するMonad
class Applicative m => Monad m where
join :: m (m a) -> m a
(>>=) :: m a -> (a -> m b) -> m b
f >>= k = join (fmap k f)
join x = x >>= id
二重に包まれた構造を潰して一重にするのがjoin
リストで言えばconcatやflattenにあたる操作
joinで実装するMonad / 具体例
instance Monad Maybe where
join Nothing = Nothing
join (Just x) = x
instance Monad [] where
join = concat
モナドは二重になった構造を潰せる高階型と考えることが出来る
<=< で実装するMonad
class Applicative m => Monad m where
(<=<) :: (b -> m c) -> (a -> m b) -> a -> m c
(>>=) :: m a -> (a -> m b) -> m b
x >>= k = (k <=< id) x
g <=< f = \a -> fmap g (f a) >>= id
合成関数の演算子.を思い出すと、
> :t (.)
(.) :: (b -> c) -> (a -> b) -> a -> c
(<=<)は型コンストラクタ付き関数結合だと思える
[Haskell] 爆速でモナドを理解する - Qiita
<=< で実装するMonad / 具体例
instance Monad Maybe where
g <=< f = \a -> case f a where
Nothing -> Nothing
Just b -> g b
instance Monad [] where
g <=< f = concatMap g . f
モナドは型コンストラクタ付き関数合成を備えた高階型と考えることが出来る
同値性
(>>=) と join と (<=<) の同値性を図で確認してみる
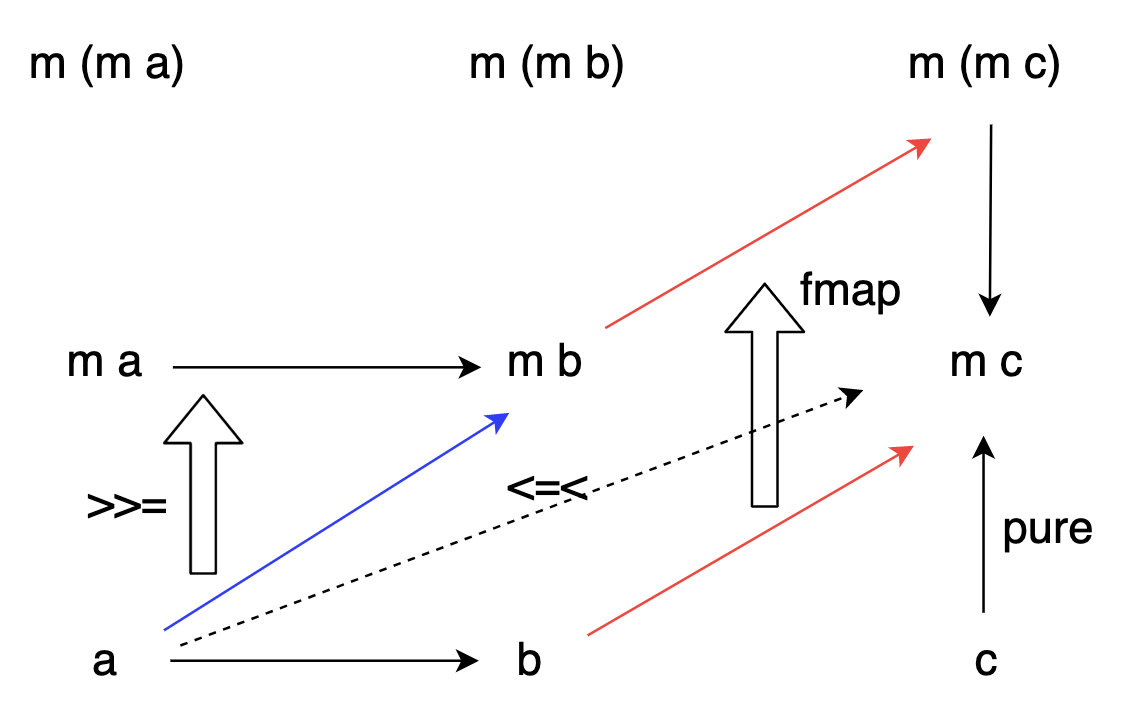
圏論の影
モナド則
任意のモナドのインスタンスは以下の関係を満たすことが要請されます
1. pure x >>= f <=> f x
2. m >>= pure <=> m
3. (m >>= f) >>= g <=> m >>= (\x -> f x >>= g)
しかしこの関係を満たしていることはコンパイラが保証してくれるものではありません
この性質はプログラムの書き換えが正しく行えることを保証してくれるので実際のプログラミングでも役に立ちます
詳しくは: モナド則とプログラミング - Qiita
このモナド則を満たす必要があるためZipListはモナドにはなれません
詳しくは: リストデータ型にのるモナド構造の単位射は a -> [a] だけ (1) - Qiita
圏論
ワドラーは批判を和らげるために、こう語っている。「モナドは単なる自己関手の圏におけるモノイド対象だよ。何か問題でも？」
不完全にしておよそ正しくないプログラミング言語小史
まとめ
まとめ
- モナドは単なる型クラス
- do構文で便利に使える
モナドを理解するためにはまず手を動かして使ってみるのが一番の近道です
モナドが手に馴染んできた暁には自分の理解の形を記事に書いて
是非モナドへの新しい登頂ルートを開拓してください！