高度合成数〜なんかよく見る数〜

高度合成数 は小さいくせに約数をたくさん持っている数です。さっそくですが顔ぶれを見てみましょう。

1, 2, 4, 6, 12, 24, 36, 48, 60, 120, 180, 240, 360, 720, 840, 1260, 1680, 2520, 5040, 7560, 10080, ... https://oeis.org/A002182

これらの数は約数をたくさん持っており割り算がしやすいので我々の日常でもよく使われるようです。
例えば1ダースの12や24時間、60分、360度などなど。

定義

自然数で、それ未満のどの自然数よりも約数の個数が多いものを高度合成数と呼びます。それっぽく書くと

自然数 $N\in{\mathbb N}$が任意の$N$より小さい自然数$N'\in{\mathbb N},\ N' < N$に対して
${\rm d}(N') < {\rm d}(N)$
を満たす時、$N$を高度合成数と呼ぶ。

ただし${\rm d}(n)$は$n$の約数の個数を与える関数（約数関数）です。
ちなみに高度合成数を最初に考案したのはあの天才数学者ラマヌジャンで、約数関数の漸近的な挙動を調べるために導入されました¹。

例えば$N=12$を考えてみると、

12 = 2^2\cdot 3

と表せるので${\rm d}(12) = 6$です（後述）。12以下の数を見てみると

$N'$	素因数分解	${\rm d}(N')$
$1$	$1$	$1$
$2$	$2$	$2$
$3$	$3$	$2$
$4$	$2^2$	$3$
$5$	$5$	$2$
$6$	$2\cdot 3$	$4$
$7$	$7$	$2$
$8$	$2^3$	$4$
$9$	$3^2$	$3$
$10$	$2\cdot 5$	$4$
$11$	$11$	$2$
$12$	$2^2\cdot 3$	$6$

となり、どれも約数の個数が6より小さいので12が高度合成数であることが分かります。

ところで自然数の約数を数える方法ですが、自然数$N$が

N = 2^{a_2} \cdot 3^{a_3} \cdot \dots \cdot p^{a_p}

のように素因数分解できる時、約数関数は

{\rm d}(N) = (1+a_2)(1+a_3) \dots (1+a_p)

のように計算することが出来ましたね²。

1000以下の自然数における${\rm d}(n)$の値をプロットすると以下のようになります。

高度合成数を赤い点でプロットしています。目で見て分かるように高度合成数は小さい方から見ていって${\rm d}(n)$の値が初めて最大値を更新するような数になってることが分かると思います。

高度合成数の性質

高度合成数はより小さい素数をより多く含む

例えば高度合成数が与えられて$q_1^{a_1}\cdot q_2^{a_2}\cdot\dots\cdot q_k^{a_k}$と素因数分解できたとします。この時、肩の指数$a_1\dots a_k$が

a_1\geq a_2 \geq \dots \geq a_k

となるように$q_1 \dots q_k$を並べ替えておきます。すると$q_1\dots q_k$にどんな素数を当てはめても約数の個数は変わらないので

{\rm d}(q_1^{a_1}\cdot q_2^{a_2}\cdot\dots\cdot q_k^{a_k}) = {\rm d}(2^{a_1}\cdot 3^{a_2}\cdot\dots\cdot p^{a_k})

となり高度合成数がこのような数の中で一番小さなものであることを考えると、$q_1=2,\cdots,q_k=p$であることが分かります。

つまり高度合成数は

2^{a_2} \cdot 3^{a_3} \cdot \dots \cdot p^{a_p}

という形に素因数分解できて、

a_2 \geq a_3 \geq \dots \geq a_p \geq 1

を満たします。より小さい素数がより多く含まれてるということですね。

参考までに高度合成数の素因数分解を小さい方からいくつか見てみましょう。

$N$	素因数分解	${\rm d}(N)$
$1$	$1$	$1$
$2$	$2$	$2$
$4$	$2^2$	$3$
$6$	$2\cdot 3$	$4$
$12$	$2^2\cdot 3$	$6$
$24$	$2^3\cdot 3$	$8$
$36$	$2^2\cdot 3^2$	$9$
$48$	$2^4\cdot 3$	$10$
$60$	$2^2\cdot 3 \cdot 5$	$12$
$120$	$2^3\cdot 3 \cdot 5$	$16$
$180$	$2^2\cdot 3^2 \cdot 5$	$18$
$240$	$2^4\cdot 3 \cdot 5$	$20$

高度合成数の最大の素因数は2個以下しか含まれない

高度合成数$N$が

N = 2^{a_2} \cdot 3^{a_3} \cdot \dots \cdot p^{a_p}

という風に素因数分解できて$a_p \geq 3$を満たすとします。

$P$を$p$の次の素数とし

N' = \frac{NP}{p^2}

と$N'$を定義します。

ベルトラン＝チェビシェフの定理（自然数$n$に対して、$n<p\leq2n$ を満たす素数$p$が存在する³）を使って$P<p^2$が成り立つことに注意すると$N'<N$が分かり、$N$が高度合成数であることより

{\rm d}(N') < {\rm d}(N)

が成り立ちます。約数関数の定義より

\begin{matrix}
&& (1+a_2)(1+a_3)\dots(1+a_p-2)(1+1) &<& (1+a_2)(1+a_3)\dots(1+a_p) \\
&\Leftrightarrow& (1+a_p-2)(1+1) &<& (1+a_p) \\
&\Leftrightarrow& 2(a_p-1) &<& (1+a_p) \\
&\Leftrightarrow& a_p &<& 3 \\
\end{matrix}

となり、これは$a_p \geq 3$という仮定に矛盾します。よって$a_p$は2以下になります。

実は**$a_p=2$となる高度合成数は4と36しかありません**。よって平方数となるような高度合成数もこの2つしか存在しません。以下ではラマヌジャンの論文¹の方法に従ってこの事実を証明していきます。

高度合成数の最大素因数が11以上の場合、最大素因数は1個しか含まれない

$p'', p', p, P, P'$で連続する素数の並びを表すことにします（例えば$2,3,5,7,11$）。

今、高度合成数$N$が

N = 2^{a_2} \cdot 3^{a_3} \cdot \dots \cdot p^{a_p}

という風に素因数分解できたとし$p\geq 11$と仮定すると、$PP'<p''p'p$が成り立つので

N' = \frac{NPP'}{p''p'p}

と置くと$N'<N$となり、高度合成数の定義より${\rm d}(N')<{\rm d}(N)$が成り立ちます。

これより、

\begin{matrix}
&&(1+a_{p''})(1+a_{p})(1+a_{p})&>&4a_{p''}a_{p'}a_{p} \\
&\Leftrightarrow&\left(1+\frac{1}{a_{p''}}\right)\left(1+\frac{1}{a_{p'}}\right)\left(1+\frac{1}{a_{p}}\right)&>&4
\end{matrix}

が成り立ちますが、もし$a_p\geq 2$だとすると、$a_{p''} \geq a_{p'} \geq a_{p} \geq 2$に注意すると

\left(1+\frac{1}{a_{p''}}\right)\left(1+\frac{1}{a_{p'}}\right)\left(1+\frac{1}{a_{p}}\right)\leq 3+\frac{3}{8}

となりますが、これは矛盾です。よって$p\geq 11$の時は$a_p=1$となることが分かりました。

高度合成数の最大素因数が5以上19以下の場合、最大素因数は1個しか含まれない

高度合成数$N$が

N = 2^{a_2} \cdot 3^{a_3} \cdot \dots \cdot p^{a_p}

という風に素因数分解できたとし、$p\geq 5$だとすると、$P<p''^3$が成り立つので

N' = \frac{NP}{p''^3}

と置けば$N'<N$となり高度合成数の定義より${\rm d}(N')<{\rm d}(N)$となるので

\begin{matrix}
&&(1+a_{p''}) &>& 2(a_{p''} - 2) \\
&\Leftrightarrow& 5 &>& a_{p''}
\end{matrix}

つまり$a_{p''} \leq 4$となることが分かります。

今$5\leq p \leq 19$だとすると$p'p>p''P$が成り立つので、

N' = \frac{Np''P}{p'p}

と置けば$N'<N$となり高度合成数の定義より${\rm d}(N')<{\rm d}(N)$となるので

\begin{matrix}
&&(1+a_{p''})(1+a_{p'})(1+a_{p})&>&2(2+a_{p''})a_{p'}a_p \\
&\Leftrightarrow&\left(1+\frac{1}{a_{p'}}\right)\left(1+\frac{1}{a_{p}}\right)&>&2\left(1+\frac{1}{1+a_{p''}}\right)
\end{matrix}

ここで先程の議論より$a_{p''}\leq 4$となることが分かっているので不等式は

\left(1+\frac{1}{a_{p'}}\right)\left(1+\frac{1}{a_{p}}\right) > 2 + \frac{2}{5}

となります。

もし$a_p\geq 2$だとすると、$a_{p'} \geq a_{p} \geq 2$に注意すると

\left(1+\frac{1}{a_{p'}}\right)\left(1+\frac{1}{a_{p}}\right) \leq 2 + \frac{1}{4}

となりますが、これは矛盾です。よって$5\leq p \leq 19$の時は$a_p=1$となることが分かりました。

平方数となるような高度合成数は4, 36のみ

これまでの結果より$p\geq 5$の時、$a_p=1$となってしまうので、平方数となるような高度合成数の候補としては$N=2^2$か$N=2^a \cdot 3^2$の形をしていなければなりません。この内$2^2=4$は既に高度合成数となることがわかっているので$N=2^a\cdot 3^2$の場合を考えましょう。$a\geq 3$と仮定して

N' = 2^{a-3}\cdot 3 \cdot 5

と置くと$N'<N$となり高度合成数の定義より${\rm d}(N')<{\rm d}(N)$となるので

\begin{matrix}
&&2(a-2) &<& 1+a \\
&\Leftrightarrow& a &<& 5 \\
\end{matrix}

よって$a$の候補は2,3,4に絞られましたが、この中で$N$が高度合成数となるのは$N=2^2\cdot 3^2=36$の場合に限られます。以上より$a_p=2$となる高度合成数は$4, 36$しか無いことがわかりました。よって平方数となるような高度合成数もこの2つに限られます。

高度合成数を列挙するアルゴリズム

されここからは話題を変えてプログラムを使って高度合成数を列挙する方法を考えてみましょう。

まず単純に考えられるアルゴリズムは定義に従って小さい方から約数の数を数えていき最大値を更新した数を記録していくというものです。

import Data.Maybe (catMaybes)
import Data.Traversable (mapAccumL)

import Data.Numbers.Primes

-- | 約数関数
d :: Integer -> Integer
d n = product [1 + countFactor n p  | p <- takeWhile (<= upperBound) primes]
  where
    upperBound = ceiling $ sqrt (fromIntegral n)
    countFactor n p = if n `mod` p == 0 then 1 + countFactor (n `div` p) p else 0

-- | 高度合成数（highly composite number）の数列
hcns :: [Integer]
hcns = catMaybes . snd $ mapAccumL go 0 [1..]
  where
    go s a = let s' = d a in if s' > s then (s', Just a) else (s, Nothing)

Repl.itの動くコードはこちら

素数の数列primesは primesというライブラリを利用しています。hcnsでは暫定の約数個数の最大値という状態を保持しながらmapする処理を実現するためにmapAccumLという関数を利用しています⁴。

実行してみると

> hcns
[1,2,4,6,12,24,36,48,60,120,180,240,360,720,840,1260,1680,2520,5040,7560,10080,15120,20160,25200,27720,

とちゃんと計算してくれますがちょっと待って出てくるのは30~40個が限界です。

実はラマヌジャンは103個の高度合成数を自力で手計算しています。コンピュータが発達した現代においてせめてそれぐらいは簡単に計算したいものです。しかしラマヌジャンも

I do not know of any method for determining consecutive highly composite numbers except by trial.

と書いている通り、効率よく高度合成数を列挙する方法を思いつくのはそう簡単なことではなさそうです。

まず考えられる方針は高度合成数を1から順番に探索するのではなく、素因数分解の形を利用して指数を変えながら探索するという方法です。これなら高度合成数は小さい素因数を多く含むという事実を使って探索空間を絞ることができ、効率が良さそうです。しかし素因数分解の形だと次に大きい候補となる数は何か、例えば素因数分解が与えられた自然数の次に大きな候補はそれを2倍したものなのか、それとも素因数2をいくつか減らして新しい素数を掛けたものなのか、を判定するのが難しい問題になってしまい小さい方から順番に調べるという戦略が取りにくくなります。

このように素因数分解の形での探索は工夫が必要なところであり、いくつものアルゴリズムが考案されています。例えばSianoによる方法⁵では最も大きい素因数を減らした場合・そのままの場合・増やした場合に分けて探索を行ったり、Kedlayaによる方法⁶では高度合成k積（highly composite k-product）という概念を利用して列挙しやすい候補のグループを作り出す方法を提案しています（こちらは実装してみたのでRepl.itに置いておきます⁷。実行してみると1から順番に調べていく単純な方法に比べてかなり速度が改善されていることがわかると思います）。

いろいろ試す中で一番実行速度が速かったのがinamoriさんのアルゴリズム⁸でした。基本的な考え方は、まず自然数を以下のような素数指数表示で考えます。

(e_1, e_2, \dots, e_m) \overset{\rm def}{=} 2^{e_1}3^{e_2}\cdots p_m^{e_m}

ただし$p_m$はm番目の素数です。この素数指数表示に対して

(e_1 + 1, e_2, \dots, e_m)

や

(e_1, e_2, \dots, e_m, e_{m+1})

といった操作で新しい候補を作成し、それが表す自然数を優先度として優先度付きキューに挿入して優先度の低い順、すなわち小さい方から高度合成数であるかを確認していくというものです。候補を作成する時はそれ以上延ばしても高度合成数にならないパターンが存在するので、そのような候補を枝刈りしていくのがポイントです⁹。以下にHaskellで実装したコードを載せておきます。

完全なコードはここをクリックすると展開されます

import Data.Function ((&))
import Data.List (find)
import Data.Maybe (catMaybes)
import Data.Traversable (mapAccumL)

import Data.Numbers.Primes
import Data.HashPSQ (HashPSQ)
import qualified Data.HashPSQ as PSQ
import Data.Vector (Vector, (!), (//))
import qualified Data.Vector as V

-- | 素数指数表示
-- 2^e2 * 3^e3 * 5^e5 * ... を <e2, e3, e5, ...> のように表す
type Exponentials = Vector Int

-- | 素数指数表示における2
two :: Exponentials
two = V.singleton 1

-- | 素数指数表示にk番目の素数を掛ける
multiplyPrime :: Exponentials -> Int -> Exponentials
multiplyPrime es k
  | k < V.length es = es // [(k, (es ! k) + 1)]
  | k == V.length es = V.snoc es 1
  | otherwise = error "今回はこのケースは起こらない"

-- | 高度合成数の候補を管理する優先度付きキュー
type Data = (Exponentials, Int)
type PQ = HashPSQ Integer Integer Data

-- | KeyとPriorityが共通で二回書くのが面倒なので関数にしておく
insertPQ :: Integer -> Data -> PQ -> PQ
insertPQ n d = PSQ.insert n n d

-- | 行き詰まりを判定するqのテーブル
qs :: [[Int]]
qs = [[ceiling (logBase (fromInteger $ primes !! k) (fromInteger $ primes !! l)) | k <- [0..]] | l <- [0..]]

-- | 行き詰まりかを判定する
isPossibleToAdd :: Exponentials -> Bool
isPossibleToAdd es = any (\k -> es ! k < 2 * qs !! V.length es !! k) possibles
  where
    possibles = [k | k <- [0..V.length es - 1], es ! k >= es ! 0 - 1]

-- | 優先度付きキューから高度合成数の候補を取り出し次の候補を挿入する
next :: PQ -> ((Integer, Data), PQ)
next pq =
  let Just (_, n, (es, m), pq') = PSQ.minView pq
      expOf2 = es ! 0
      insert1 = insertPQ (n * primes !! V.length es) (es `multiplyPrime` (V.length es), 2 * m)
      insert2 = case find (\i -> es ! i == expOf2 - 1) [1..V.length es - 1] of
                  Nothing -> id
                  Just k -> insertPQ (n * primes !! k) (es `multiplyPrime` k, m `div` expOf2 * (expOf2 + 1))
      insert3 = insertPQ (n * 2) (es `multiplyPrime` 0, m `div` (expOf2 + 1) * (expOf2 + 2))
      pq'' = pq'
        & (if expOf2 == 1 then insert1 else id)
        & (if isPossibleToAdd es then insert3 . insert2 else id)
   in ((n, (es, m)), pq'')

-- | 高度合成数の数列
hcns :: [Integer]
hcns = catMaybes . snd $ mapAccumL f 0 $ iterate' next $ PSQ.singleton 2 2 (two, 2)
  where
    iterate' :: (a -> (b, a)) -> a -> [b]
    iterate' f a = map fst . tail $ iterate (f . snd) (undefined, a)
    f maxD (hcn, (ps, m)) = if maxD < m then (m, Just hcn) else (maxD, Nothing)

main :: IO ()
main = mapM_ print $ take 1000 hcns

指数の配列を管理するのにvectorと、優先度付きキューのライブラリとしてpsqueuesを使用しています¹⁰。

隣り合う高度合成数の比

隣り合う高度合成数の比は1に収束することをラマヌジャンは証明しています。せっかく高度合成数を列挙出来るようになったのでその様子を図示してみましょう。

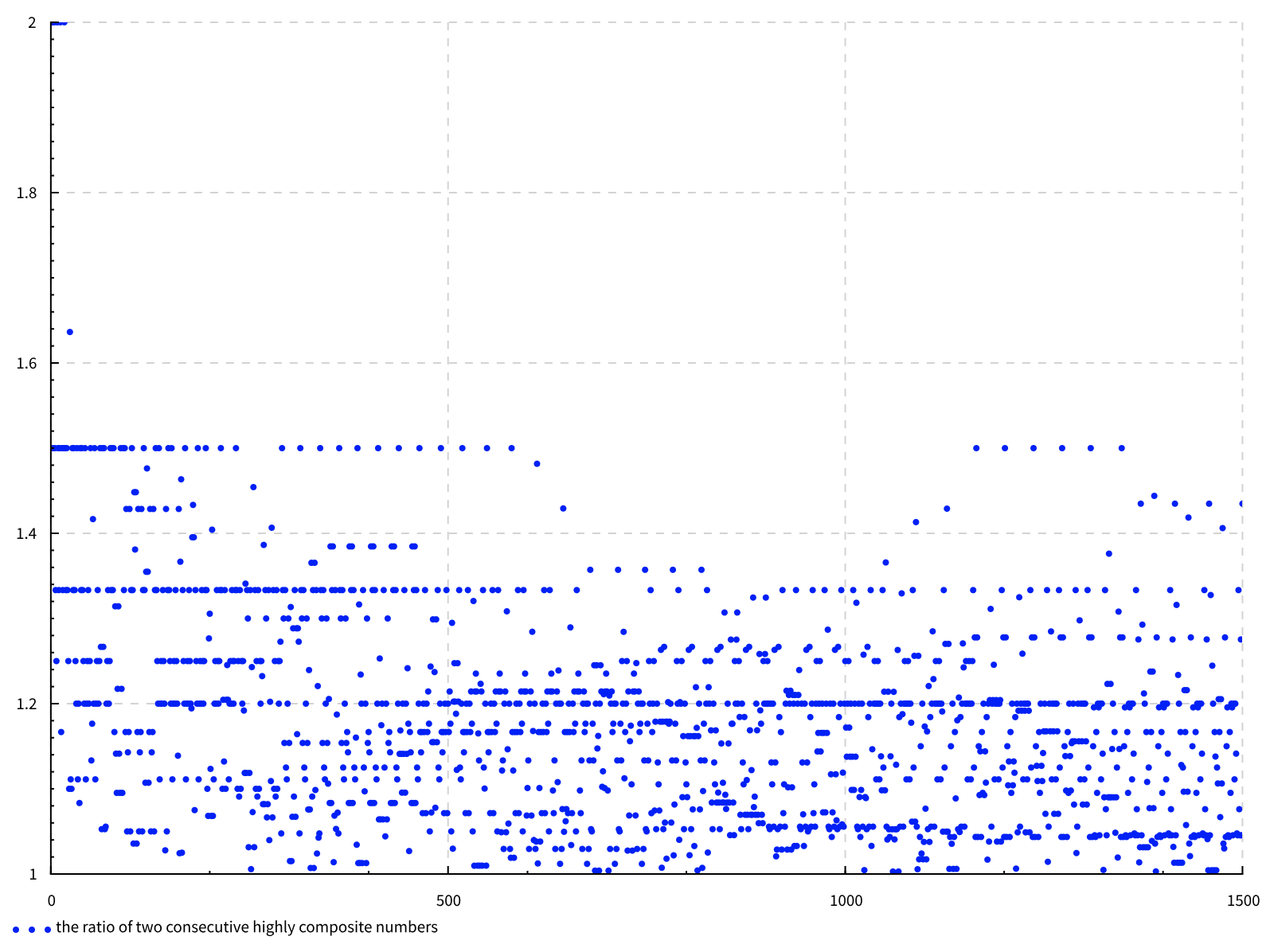
縦軸が隣り合う高度合成数の比で横軸は何番目の高度合成数であるかを表しています。実はSianoの論文⁵にn=1000までの図が載っていて1に収束していくように見えたのですが、今回1500まで出してみると1200あたりでまた盛り上がりがあるのが見てわかると思います。1に近づいて行くのは本当にゆっくりみたいですね。

優高度合成数

自然数$N\in{\mathbb N}$に対してある正の実数$\epsilon$が存在し、任意の自然数$N'\in{\mathbb N}$に対して
$\frac{{\rm d}(N)}{N^\epsilon}\geq\frac{{\rm d}(N')}{N'^\epsilon}$
が成り立つ時、$N$を優高度合成数と呼ぶ。

この優高度合成数という概念もラマヌジャンによって導入されたものです¹。どうしてこのような数に高度合成数という名前が含まれているのかというと、実は優高度合成数であれば自動的に高度合成数になってしまうことが分かるからです。

$N$を優高度合成数とすると、ある正の実数$\epsilon$が存在し、任意の自然数$N'\in{\mathbb N}$に対して

\frac{{\rm d}(N)}{N^\epsilon}\geq\frac{{\rm d}(N')}{N'^\epsilon}

が成り立つことが優高度合成数の定義でしたが、これを式変形すると特に$N'<N$となるような$N'$に対して

{\rm d}(N)\geq\left(\frac{N}{N'}\right)^\epsilon{\rm d}(N') > {\rm d}(N')

が成り立つため$N$が高度合成数であることが分かりました。

ところで優高度合成数は本当に存在するんでしょうか？高度合成数はその数よりも小さい数に対して条件が成り立てば良かった一方で、優高度合成数はさらに無限に多く存在するその数よりも大きい数に対しても条件が成り立つことが要求されます。約数の個数は無限に大きくなりうる中で$\frac{{\rm d}(N)}{N^\epsilon}$は本当に最大値を持つのでしょうか？

実は約数関数は任意の正の実数$\epsilon$に対して

{\rm d}(n) = o(n^\epsilon)

が成り立つことが知られています。このことから、$\frac{{\rm d}(N)}{N^\epsilon}$は$\epsilon$がどんな値であっても$N$が大きくなればちゃんと0に収束していくことが分かります。つまり$\frac{{\rm d}(N)}{N^\epsilon}$は$N$が小さいうちは特に高度合成数の${\rm d}(N)$が増加していくので一度盛り上がりますが、$N$が大きくなってくると$N^\epsilon$の方が速く大きくなり全体として下がっていくような形をしているのです。$\epsilon$の値を変えることで減少に転じるポイントも変わり、この点こそが優高度合成数に対応しているのです。例えば$\epsilon=0.4$の時は以下のようなグラフになります。

横軸は自然数で縦軸は$\frac{{\rm d}(N)}{N^\epsilon}$の値です。優高度合成数は赤い点、高度合成数はオレンジ色の点、その他の数は青い点で表しています。
さらに$\epsilon$を変化させて行くと以下のように変化していきます。

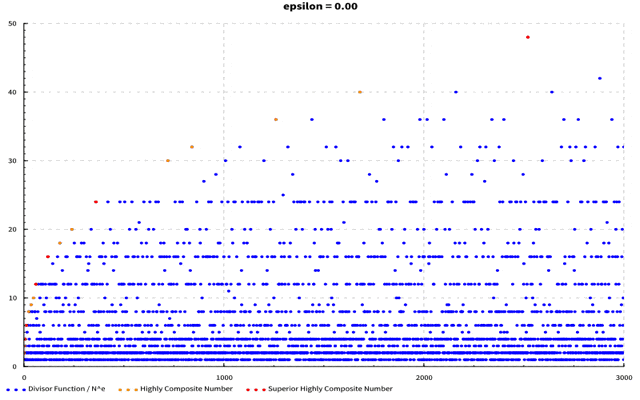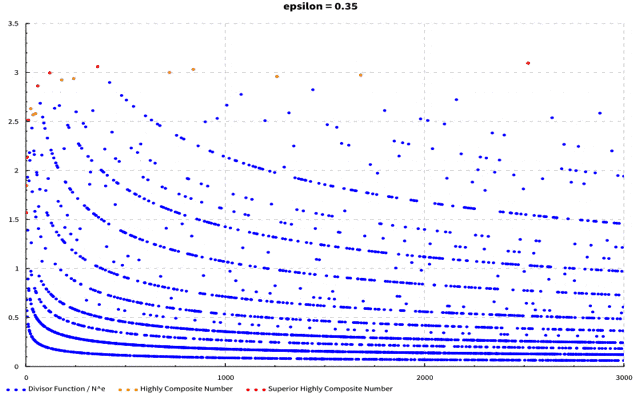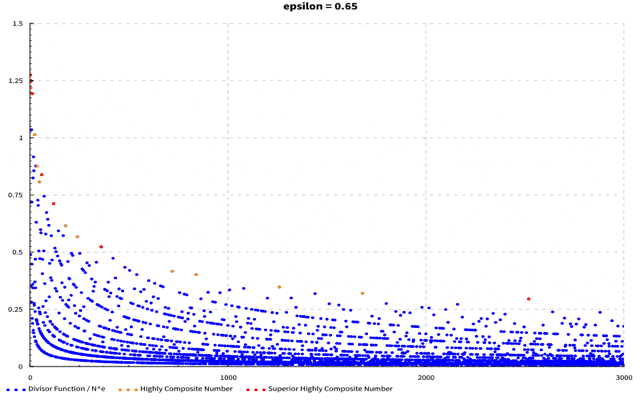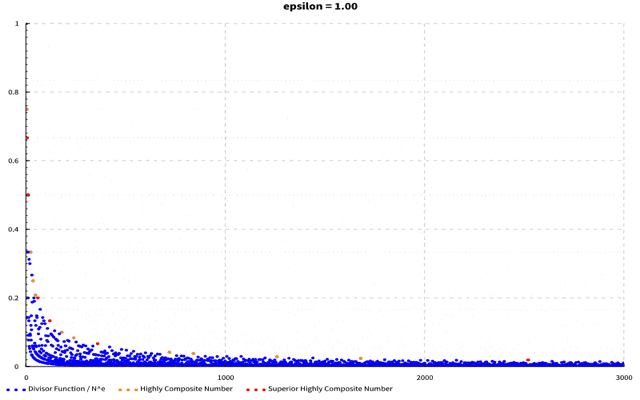
（軸がブレててすみません…）$\epsilon$を0~1まで0.05刻みに動かしています。$\epsilon$が大きくなるに従って最大値を取る点が左に動いていくのが分かるかと思います。

優高度合成数を具体的に列挙すると以下のようになります。

$N$	素因数分解	${\rm d}(N)$
$2$	$2$	$2$
$6$	$2\cdot 3$	$4$
$12$	$2^2\cdot 3$	$6$
$60$	$2^2\cdot 3 \cdot 5$	$12$
$120$	$2^3\cdot 3 \cdot 5$	$16$
$360$	$2^3\cdot 3^2 \cdot 5$	$24$
$2520$	$2^3\cdot 3^2 \cdot 5 \cdot 7$	$48$
$5040$	$2^4\cdot 3^2 \cdot 5 \cdot 7$	$60$
$55440$	$2^4\cdot 3^2 \cdot 5 \cdot 7 \cdot 11$	$120$
$720720$	$2^4\cdot 3^2 \cdot 5 \cdot 7 \cdot 11 \cdot 13$	$240$

出典: Superior highly composite number - Wikipedia

このように優高度合成数は無限に¹¹続いていきます。

ところで隣り合う優高度合成数の比を見てみると、

\begin{matrix}
\frac{6}{2} &=& 3 \\
\frac{12}{6} &=& 2 \\
\frac{60}{12} &=& 5 \\
\frac{120}{60} &=& 2 \\
\frac{360}{120} &=& 3 \\
\frac{2520}{360} &=& 7 \\
\frac{5040}{2520} &=& 2 \\
\frac{55440}{5040} &=& 11 \\
\frac{720720}{55440} &=& 13 \\
\end{matrix}

これまでのところ全て素数になっていることが分かります！全ての隣り合う優高度合成数の比は素数になるのでしょうか？

またところで、高度合成数の定義における約数の個数を約数の総和を元の自然数で割ったものに置き換えて定義される数を超過剰数と呼びます。すなわち

自然数 $N\in{\mathbb N}$が任意の$N$より小さい自然数$N'\in{\mathbb N},\ N' < N$に対して
$\frac{{\rm \sigma}(N')}{N'} < \frac{{\rm \sigma}(N)}{N}$
を満たす時、$N$を超過剰数と呼ぶ。

ただし、${\rm \sigma}(N)$は$N$の約数の総和を与える関数です。この超過剰数は高度合成数と関係が深いことが知られています。小さい方からいくつか列挙してみると、

1, 2, 4, 6, 12, 24, 36, 48, 60, 120, 180, 240, 360, 720, 840, 1260, 1680, 2520, 5040, 10080, ... https://oeis.org/A004394

という感じで、ここに現れている数は全て高度合成数です。冒頭の高度合成数の列挙に比べると7560だけが欠けているのが分かります。

同様に優高度合成数と関係の深い巨大過剰数（Colossally abundant number）という数も存在します。小さい方から列挙してみると

2, 6, 12, 60, 120, 360, 2520, 5040, 55440, 720720, ... https://oeis.org/A004490

という感じで、ここに現れている数は全て優高度合成数でもあります。

そうなると優高度合成数と同様に隣り合う巨大過剰数の比は常に素数となるのか？という疑問が考えられますが、実はこれは未解決予想になっています。この予想は1944年にAlaogluとErdősによって発表され未だに未解決のままなのです。この問題は同様に未解決予想である四指数予想の特別な場合として従うそうです。

おわり

人間生きていると特に根拠となるものも無いのに何か数を決めないといけないという場面に出くわすものです。そんな時はマジックナンバーとして高度合成数を採用すれば後々計算が楽になって便利かもしれません。みなさんもいざという時は高度合成数を積極的に役立ててみてください

1. http://ramanujan.sirinudi.org/Volumes/published/ram15.pdf ↩ ↩² ↩³

2. わかりやすい解説はこことか 約数の個数の公式と平方数の性質 ↩

3. 一松先生のわかりやすい証明がこちら "nと2nの間に素数がある-ベルトラン・チェビシェフの定理のエルデーシュによる初等的証明-" ↩

4. @fumieval 氏にアドバイス頂きました。ありがとうございます！ ↩

5. Siano, D. B., and J. D. Siano. "An algorithm for generating highly composite numbers." ↩ ↩²

6. Kedlaya, Kiran S. "An Algorithm for Computing Highly Composite Numbers" ↩

7. なぜか48だけ出力されないので誰か原因わかったら教えてください… ↩

8. ラマヌジャンの高度合成数 - 桃の天然水 ↩

9. Project Euler 110（2） - 桃の天然水 ↩

10. 優先度付きキューのライブラリは @kakkun61 氏に教えて頂きました。ありがとうございます！ ↩

11. 無限にあるんでしたっけ…？ ↩