この記事はCAMPHOR- Advent Calendar 2018の19日目の記事です。
データ構造とアルゴリズム Advent Calendar 2018の12日目の記事である"「アルゴリズムこうしん」のアルゴリズムを作成する"にインスパイアされて、Haskellで実装するとどうなるか考えてみました。
"アルゴリズムこうしん"とは
アルゴリズムこうしんとは、NHK教育「ピタゴラスイッチ」の中で行われる体操のようなレクリエーションである。
(引用: ニコニコ大百科 - アルゴリズムこうしん)
アルゴリズムこうしんは二人で一連の動作を組み合わせて行う体操で、フローチャートに起こすと以下のような感じです。
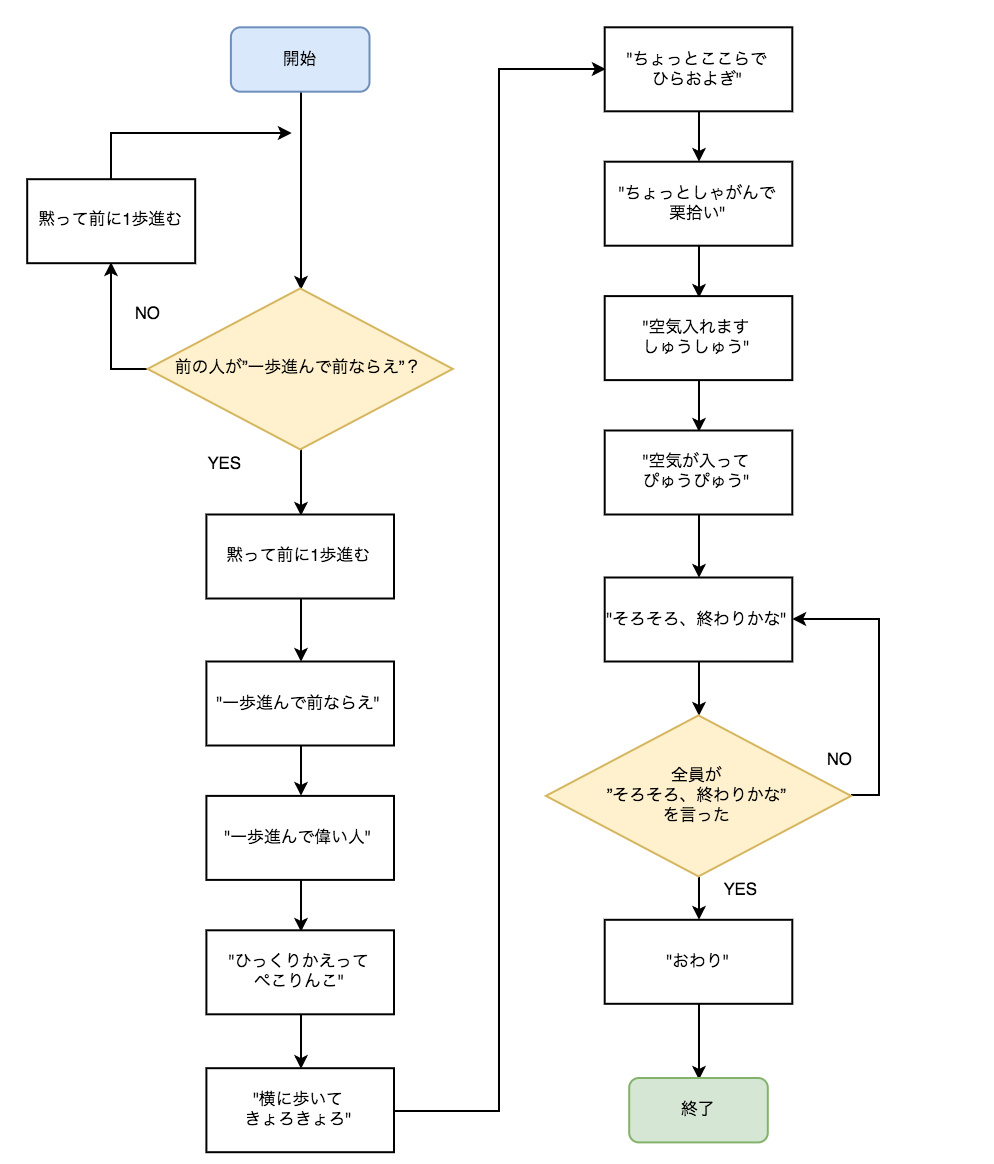
まぁフローチャートを眺めるよりも動画を見たらすぐに分かると思います。
通常は二人で行う体操ですが、二人である必然性はありません。この記事ではn人で行うアルゴリズムこうしんのアルゴリズムをプログラムを使って実装していきます。
"アルゴリズムこうしん"のアルゴリズム
アルゴリズムこうしんのアルゴリズムの面白いところは
- "1歩進んで前ならえ"を行う前に、前の人の行動を確認する必要がある
- "おわり"と言う前に、全員の行動を確認する必要がある
というように、一見するとシーケンシャルに行われているように見える一人ひとりの行動の中に、他の人の行動に依存する部分が現れるところです。この依存関係をどのようにモデリングしていくかが実装の鍵となるところでしょう。
あらかじめ各人が全員の人数を知っている場合
アルゴリズムこうしんを行う人たち全員があらかじめ
- 全員の人数
- 自分が何番目であるか
を把握している場合は分岐する箇所の繰り返しの数が計算できるので、前述した依存関係は見かけだけのものとなり、単純なシーケンス処理として実装することができます。
data Action = Empty
| Maenarae
| Eraihito
| Pekorinko
| Kyorokyoro
| Hiraoyogi
| Kurihiroi
| Shushu
| Pyupyu
| Owarikana
| Owari
deriving (Show, Eq, Ord, Enum)
まずは人の行動を列挙してデータ構造にしました。
say :: Action -> String
say Empty = ""
say Maenarae = "1歩進んで前習え"
say Eraihito = "1歩進んで偉い人"
say Pekorinko = "ひっくりかえってぺこりんこ"
say Kyorokyoro = "横に歩いてきょろきょろ"
say Hiraoyogi = "ちょっとここらでひらおよぎ"
say Kurihiroi = "ちょっとしゃがんで栗拾い"
say Shushu = "空気入れますしゅうしゅう"
say Pyupyu = "空気がはいってぴゅうぴゅう"
say Owarikana = "そろそろ、終わりかな"
say Owari = "おわり"
次にそれぞれの行動時におけるセリフの実装です。
actions :: Int -> Int -> [Action]
actions n i = concat $ [ replicate i Empty
, [ Maenarae
, Eraihito
, Pekorinko
, Kyorokyoro
, Hiraoyogi
, Kurihiroi
, Shushu
, Pyupyu
]
, replicate (n-i) Owarikana
, [Owari]
]
最後に全体の人数と自分が何番目か(0始まり)を与えると一連の動作の列を返してくれる関数です。実際にこれを使ってアルゴリズムこうしんを行ってみましょう。
main :: IO ()
main = do
let n = 2
mapM_ putStrLn .
map (intercalate " / " . map say) .
transpose $ map (actions n) [0..n-1]
実装はふーんと思って見ておいてもらえれば大丈夫です1。実行すると
$ runhaskell Main.hs
1歩進んで前習え /
1歩進んで偉い人 / 1歩進んで前習え
ひっくりかえってぺこりんこ / 1歩進んで偉い人
横に歩いてきょろきょろ / ひっくりかえってぺこりんこ
ちょっとここらでひらおよぎ / 横に歩いてきょろきょろ
ちょっとしゃがんで栗拾い / ちょっとここらでひらおよぎ
空気入れますしゅうしゅう / ちょっとしゃがんで栗拾い
空気がはいってぴゅうぴゅう / 空気入れますしゅうしゅう
そろそろ、終わりかな / 空気がはいってぴゅうぴゅう
そろそろ、終わりかな / そろそろ、終わりかな
おわり / おわり
※左が行進の先頭になっていることに注意してください
うまくいきましたね!こちらのアルゴリズムが元の記事によるものに近いものになっていると思います。
制御フローを分離する
アルゴリズムこうしんは各人が全体を把握していなくても適当に人をごちゃっと集めてきて一列に並べてスタートさせたら上手くいくアルゴリズムです。全員が何人か知らなくても、自分が前から何番目かも知らなくてもうまく動くようなプログラムを考えたいと思うのは自然でしょう。それはつまりアルゴリズムこうしんのアルゴリズムを
- 制御フロー
- 各人が行うべき行動を判断する処理
の2つに分離するということです。しかし前述したように、アルゴリズムこうしんのアルゴリズムには他人の行動に依存する処理が存在するので、単純に判断の処理だけを分離するわけには行きません。
アルゴリズムこうしんの制御フローを改めて図示すると下図ようになるでしょう。赤矢印の順番が実際に処理が行われる順番に対応しています。

各人が次の行動を判断する時に知らないといけない情報は
- 前の人の行動
- 全員が"そろそろ終わり"なのかどうか
(これは後ろの人の行動がわかれば十分)
そして
- 自分が一つ前にとった行動
の3つです。これらの依存関係を図示すると

このようになり、3方向からのデータの流れを実現する必要があることがわかります。
前の人の行動を知る
まず右矢印(→)のデータの流れから考えましょう。これは制御フローの順番にデータが流れてくるため、前の人のActionを受け取って何らかの計算をしたあとに自分のActionを返す関数として定義できそうです。
Action -> (a, Action)
Stateモナドは状態を受け取って状態を返すパターンを抽象化したもので
type State s a = s -> (a, s)
のような型をしています。
例えばグローバルな変数をインクリメントしていく
increment :: State Int ()
increment s -> ((), s + 1)
という関数を考えるとします。これを使えば3回インクリメントする処理は、
let s0 = 0
(_, s1) = increment s0
(_, s2) = increment s1
(_, s3) = increment s2
in s3
というように記述できます。このような"関数の返り値から状態を取り出して次の関数の引数に渡す"というパターンを抽象化してdo構文(モナド)の中に押し込めたのがStateモナドです。もしincrementがStateモナドで記述されていれば以下のような実装を書くことができるでしょう。
s3 = flip execState 0 $ do
increment
increment
increment
-- s3 == 3
過去の自分の行動を知る
次に下矢印(↓)のデータの流れを考えましょう。自分自身の一つ前の行動ではありますが計算は制御フロー図の赤い矢印の順番に行われるため、上手くデータを渡すための工夫をする必要があります。もちろん既にStateモナドを導入しているので"今までの全ての行動を保存して検索する"という実装も考えられますが、管理が大変だし本来知る必要のない情報にもアクセスできるようになってしまうので可能であれば避けたい方法です。もしオブジェクトのような概念を作れる言語であれば人をインスタンスとして管理し、メモリ上に前の行動を載せておくことを考えるでしょう。そこでHaskellでも同じようにIORefを使ってメモリ上に前の人のActionを保存して過去の自分の行動を受け取ることにしましょう5。
IORefは変更可能な変数への参照を表す型です。基本的な操作として
newIORef :: a -> IO (IORef a) -- 新規作成
readIORef :: IORef a -> IO a -- データの読み込み
writeIORef :: IORef a -> a -> IO () -- データの書き込み
というものがあります。例えば参照先の値をインクリメントする関数は
increment :: IORef Int -> IO ()
increment ref = do
a <- readIORef ref
writeIORef (a + 1)
というように書け6、これを使って3回インクリメントする処理は
do
ref <- newIORef 0
increment ref
increment ref
increment ref
a <- readIORef ref
print a -- 3
のように実装することができます。
後ろの人の行動を知る
最後に左矢印(←)のデータの流れを考えましょう。これは制御フローに対してデータの流れが完全に逆行しているため、普通に考えると為す術がないように見えます。しかし後続の処理の結果が必要なのだと考えると、継続という概念を使えば実装することができそうです。ここでは継続モナドを使って継続の概念を扱って行きましょう78。
継続モナドは
type Cont r a = (a -> r) -> r
という型をしています。例えばこれを使って与えられた数のリストを掛け算する関数を実装すると
prod :: [Int] -> Cont Int Int
prod [] = \k -> k 1
prod (0:_) = \_ -> 0
prod (x:xs) = \k -> x * prod xs k
のように実装できます。kにはこれから継続する計算が入ってるのがポイントです。例えば[1,2,3]の積は
prod [1,2,3] id = (\k -> 1 * prod [2, 3] k) id
= 1 * prod [2, 3] id
= 1 * (\k -> 2 * prod [3] k) id
= 1 * (2 * prod [3] id)
= 1 * (2 * (\k -> 3 * prod [] k) id)
= 1 * (2 * (3 * prod [] id))
= 1 * (2 * (3 * id 1))
= 1 * (2 * (3 * 1))
= 1 * (2 * 3)
= 1 * 6
= 6
のように計算されます。途中1 * (2 * (3 * id 1))になっているところを見ると後続する計算を行ったあとに自分自身の数を掛けるという構造が現れているのがわかるかと思います。特に0が含まれる掛け算のリストでは継続が捨てられるので、後続の計算という考え方が分かりやすいかもしれません。
prod [1,0,error "unreachable"] id = (\k -> 1 * prod [0, error "unreachable"] k) idid
= 1 * prod [0, error "unreachable"] id
= 1 * (\ _ -> 0) id
= 1 * 0
= 0
0のところで見事に継続が捨てられており後続の計算で使用されるはずのerrorまで到達しないのがわかります。
継続モナドは継続をコールバック関数としてスタックに積み上げて、最後にスタックを上から(すなわち実行時と逆順に)実行していく仕組みと考えると分かりやすいかもしれません8。
全てを組み合わせる
以上の考察より
- Stateモナド
- IORef
- 継続モナド
の3つを組み合わてデータの流れを実現すればアルゴリズムこうしんを実装することができそうです。これら3つのモナドを組み合わせるためにモナドトランスフォーマー910を使います。実際に実装したプログラムが以下になります。
type LastAction = Action -- 過去の自分の行動
type PrevAction = Action -- 前の人の行動
type NextAction = Action -- 後ろの人の行動
actor :: IORef LastAction -> ContT NextAction (StateT PrevAction IO) ()
actor actRef = do
prevAct <- lift get -- 前の人の行動を取得
lastAct <- liftIO $ readIORef actRef -- 自分の直前の行動を取得
let myAct = case (lastAct, prevAct) of
(Empty, Eraihito) -> Maenarae -- 前の人が偉い人をしたら"前ならえ"
(Empty, _ ) -> Empty -- そうじゃなければ無言で進み続ける
(Owarikana, _ ) -> Owarikana -- "終わりかな"は一旦繰り返す
_ -> succ lastAct -- それ以外の場合は次の行動を取る
lift $ put myAct -- 自分の行動を後ろの人に伝える
ContT $ \k -> do
nextAct <- k myAct -- 継続を使って後ろの人の行動を知る
let myAct' = case (lastAct, nextAct) of
(Owarikana, Owari) -> Owari -- "終わりかな"の時は後ろの人が"おわり"なら自分も終わる
_ -> myAct -- それ以外の場合は行動を変えない
liftIO $ writeIORef actRef myAct' -- 自分の行動を更新する
pure myAct' -- 自分の行動を前の人に伝える
pure ()
制御フローに言及せず局所的な情報のみを使ってアルゴリズムを実装できているのがわかるかと思います。実装がどうしても複雑になってしまうのは"アルゴリズムこうしん"に内在する複雑さと、後述するように必要十分な抽象化を選択できていない可能性があるからだと思います。実際に制御フローを実装して実行してみましょう。
main :: IO ()
main = do
-- 前の行動を表す変数をEmptyで初期化する
actRef1 <- newIORef Empty
actRef2 <- newIORef Empty
fix $ \loop -> do
-- アルゴリズムこうしんを1ステップ進める
(flip runStateT Eraihito) .
(flip runContT (const $ pure Owari)) $ do
actor actRef1 -- 一人目
actor actRef2 -- 二人目
-- 1ステップのアルゴリズムこうしんの結果を取得し表示する
actions <- mapM readIORef [actRef1, actRef2]
putStrLn $ intercalate " / " $ map say actions
-- アルゴリズムこうしんの終了条件を確認する
if all (== Owari) actions
then pure () -- 全員が"おわり"なら終了する
else loop -- そうでなければ繰り返す
$ runhaskell Main.hs
1歩進んで前習え /
1歩進んで偉い人 / 1歩進んで前習え
ひっくりかえってぺこりんこ / 1歩進んで偉い人
横に歩いてきょろきょろ / ひっくりかえってぺこりんこ
ちょっとここらでひらおよぎ / 横に歩いてきょろきょろ
ちょっとしゃがんで栗拾い / ちょっとここらでひらおよぎ
空気入れますしゅうしゅう / ちょっとしゃがんで栗拾い
空気がはいってぴゅうぴゅう / 空気入れますしゅうしゅう
そろそろ、終わりかな / 空気がはいってぴゅうぴゅう
そろそろ、終わりかな / そろそろ、終わりかな
おわり / おわり
うまく動いていますね ![]()
これをn人に拡張したければactorの数をn個まで増やせば良いのですが、コピペするのは行儀が良くないので変数で変えられるようにプログラムを修正しましょう。
main :: IO ()
main = do
let n = 3
-- 前の行動を表す変数をEmptyで初期化する
actRefs <- sequence . replicate n $ newIORef Empty
fix $ \loop -> do
-- アルゴリズムこうしんを1ステップ進める
(flip runStateT Eraihito) .
(flip runContT (const $ pure Owari)) .
sequence $ map actor actRefs
-- 1ステップのアルゴリズムこうしんの結果を取得し表示する
actions <- mapM readIORef actRefs
putStrLn $ intercalate " / " $ map say actions
-- アルゴリズムこうしんの終了条件を確認する
if all (== Owari) actions
then pure () -- 全員が"おわり"なら終了する
else loop -- そうでなければ繰り返す
$ runhaskell Main.hs
1歩進んで前習え / /
1歩進んで偉い人 / 1歩進んで前習え /
ひっくりかえってぺこりんこ / 1歩進んで偉い人 / 1歩進んで前習え
横に歩いてきょろきょろ / ひっくりかえってぺこりんこ / 1歩進んで偉い人
ちょっとここらでひらおよぎ / 横に歩いてきょろきょろ / ひっくりかえってぺこりんこ
ちょっとしゃがんで栗拾い / ちょっとここらでひらおよぎ / 横に歩いてきょろきょろ
空気入れますしゅうしゅう / ちょっとしゃがんで栗拾い / ちょっとここらでひらおよぎ
空気がはいってぴゅうぴゅう / 空気入れますしゅうしゅう / ちょっとしゃがんで栗拾い
そろそろ、終わりかな / 空気がはいってぴゅうぴゅう / 空気入れますしゅうしゅう
そろそろ、終わりかな / そろそろ、終わりかな / 空気がはいってぴゅうぴゅう
そろそろ、終わりかな / そろそろ、終わりかな / そろそろ、終わりかな
おわり / おわり / おわり
これで何人でもアルゴリズムこうしんができるようになりましたね!
まとめ
アルゴリズムこうしんのアルゴリズムを制御フローと局所的な処理に分離してうまく記述することができました。ただ以下の点についてはまだ改善の余地があるのかなと思っています。
- 前の自分の行動を知るのに本当に
IOが必要か? - 後ろの人の行動を知るのに本当に継続が必要か?
IOも継続も強力な概念なのでアルゴリズムを実装するために十分な能力を持っているのですが必要最低限ではないので、自由度が高い分だけ意図しない挙動を実装してしまう可能性が高くなります。また機会があれば必要十分な抽象化についても考えてみたいですね。
今回作ったプログラムはgistにも公開しているので実際に動かして遊んでみてください。
-
modifyIORefを使えばincrement = flip modifyIORef (+1)と書けます ↩