確率とモナドと確率的プログラミング

この記事はADVANCED BEGINNERからCOMPETENTの方を対象読者として書かれています。

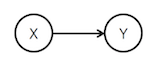
コインの裏表やサイコロの出目はよく確率変数によって表されます。確率変数が互いに依存しているようなモデルを記述する手法としてグラフィカルモデルと云うものがあります。例えば、ある分布に従って表が出る確率が偏ったコインが選ばれた後、そのコインを投げて表裏が決まるような実験を考えた場合、コインの確率変数を $X$, コインの表裏の確率変数を $Y$ とすると、この系を記述するグラフィカルモデルは

このようになります。ところで $X$ は表が出る確率Double上の確率変数RVar Doubleで、 $Y$ は $X$ の結果に依存したコインの裏表Bool上の確率変数Double -> RVar Boolであると考えるとします。今コインがランダムに選ばれると言う構造を 忘れて コインの表裏が出る確率変数RVar Boolを知りたいと思うと

RVar Double -> (Double -> RVar Bool) -> RVar Bool

このような関数が欲しくなるのではないでしょうか。お気付きの通りこれはモナドの(>>=)を思い出させるような形をしていて、実際RVarはモナドのインスタンスとなるように作ることができます。

確率分布はモナドだ

確率変数RVarを考える前に確率分布Distを考えることにしましょう。さらに実装の簡便さからここでは離散確率分布を考えます。

type Prob = Double
newtype Dist a = Dist [(a, Prob)]

確率分布は確率変数のとる値から $[0,1]$ への関数ですが、Distはそのグラフとなるように定義しています。Probは単なるDoubleのエイリアスですが、値が $[0,1]$ を取ることを期待されるものとします。今、f :: a -> bなる関数があってa上の確率分布が与えられている時に、b上の確率分布Dist bをDist aから生成した値にfを適用して得られたbの分布と考えると

instance Functor Dist where
  fmap f (Dist as) = Dist [(f a, p) | (a, p) <- as]

この様にDistがFunctorのインスタンスになることがわかります。

次にf :: a -> bが確率分布Dist (a -> b)から確率的に生成されていたとして同時にa上の確率分布Dist aが与えられていた時に、それぞれから生成された値を適用したf a :: b上の分布を考えると

instance Applicative Dist where
  pure x = Dist [(x, 1.0)]
  (Dist fs) <*> (Dist as) = Dist [(f a, p * q) | (f, p) <- fs, (a, q) <- as]

この様にApplicativeのインスタンスも定義できると思います。ちなみにこれを使って

joint :: Dist a -> Dist b -> Dist (a, b)
joint da db = (,) <$> da <*> db

このようなaとbの同時分布を求める関数を書くことができます。

最後に確率分布Dist a上の確率分布、すなわちDist (Dist a)を考えてみましょう。Dist (Dist a)から値（確率分布）を生成し、さらに生成された確率分布からaの値を生成することを考えると

join :: Dist (Dist a) -> Dist a
join ass = Dist [(a, p * q) | (Dist as, p) <- ass, (a, q) <- as]

この様にa上の確率分布上の確率分布からa上の確率分布を得る関数を作ることができます。これを使えば

instance Monad Dist where
  m >>= k = join (fmap k m)

DistをMonadのインスタンスにすることができました。

Distを使った簡単な例を見てみましょう。サイコロの出目の確率分布diceを以下のように定義します。

dice :: Dist Int
dice = Dist $ map (\x -> (x, 1/6)) [1..6]

これを使って2つのサイコロの目の和を表す確率分布がどのようになるのかを計算してみます。その前に確率分布を表示する関数を作っておきましょう。

showDist :: (Show a, Ord a) => Dist a -> String
showDist (Dist as) =
  show .
    map (\as -> (fst (head as), sum (map snd as))) .
      groupBy (\a b -> fst a == fst b) .
        sort $ as

ここで作ったDistの実装ではaの同じ値が中のリストに複数個現れてしまうのでうまくグループ化して確率を足して重複を無くした後に表示するようにしています。これらを使えば

Main.hs

main :: IO ()
main = do
  putStrLn $ showDist $ do
    x <- dice
    y <- dice
    pure (x + y)

$ runhaskell Main.hs
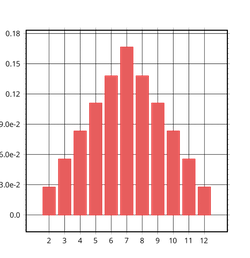
[(2,2.7777777777777776e-2),(3,5.555555555555555e-2),(4,8.333333333333333e-2),(5,0.1111111111111111),(6,0.1388888888888889),(7,0.16666666666666669),(8,0.1388888888888889),(9,0.1111111111111111),(10,8.333333333333333e-2),(11,5.555555555555555e-2),(12,2.7777777777777776e-2)]

この様に２つのサイコロの目の和を表す確率分布を作ることができました。

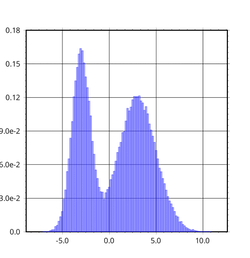
さて、確率変数の話に戻りましょう。RVarという型は実際rvarというHackageの中で定義されていて, RVarがモナドのインスタンスになることは確率分布がモナドのインスタンスになることを使って定義されています。random-fuというHackageではよく知られた確率分布とそれに従う確率変数が定義されており、当然連続なものもたくさんあります。例えばこれを使って混合ガウス分布に従うような確率変数は

import Data.Random
import Data.Random.Distribution.Dirichlet
import Data.Random.Distribution.Exponential
import Data.Random.Distribution.Categorical

gaussianMixtureModel :: [Double]           -- 各正規分布の係数
                     -> [(Double, Double)] -- 各正規分布のパラメータ
                     -> RVar Double
gaussianMixtureModel weights params = do
  let gs = map (\(mu, sigma) -> normal mu sigma) params
  selected <- categorical $ zip weights gs
  selected

main :: IO ()
main = do
  results <- sample $ do
    weights <- dirichlet [1, 1]
    params <- sequence $ replicate (length weights) $ do
      mu <- normal 0 10
      sigma <- exponential 1
      pure (mu, sigma)
    sequence $ replicate 1000 $ gaussianMixtureModel weights params
  print results

このように定義することができます。グラフィカルモデルがもつDAGの構造をモナドを使って綺麗に記述できているのが分かると思います。

参考

• [A Probabilistic Functional Programming Library for Haskell] (http://web.engr.oregonstate.edu/~erwig/pfp/)
• プログラミングのための確率統計 in Haskell
• FUNCTIONAL PEARLS: Probabilistic Functional Programming in Haskell
• Giry monad in nLab

確率的プログラミング言語

グラフィカルモデル（特にここではDAGとなるものを扱うのでベイジアンネットワーク）を考えた時に実際に生成された値からモデルを構成する確率変数の確率分布を推定するのは重要な問題です。簡単な例で言えばあるデータが正規分布に従っていると仮定した時に実際に得られたデータからその平均と分散の値を求めるといったような問題です。それぞれの確率モデルごとに最適な推定アルゴリズムは違っていますが、問題に合わせて逐一実装するのは少々面倒でしょう。さらに複雑な確率モデルになっても最適な推定アルゴリズムが存在するとは限りません。そこでデータが得られた後の事後分布をサンプリングされた点列で近似することを考えます。この方法ならモデルがある程度複雑になっても同じ方法で近似的に事後分布を得ることができます。

このような確率モデルを構築してサンプリングによって事後確率分布を推定するというプロセスは色々な問題に共通して使うことができます。確率的プログラミングはプログラムによって確率モデルを記述し、実行としてサンプリングを行って推定結果が出力されるというアプローチでこれらの問題を統一的に扱います。確率的プログラミング言語はたくさん存在していて、古くからあるBUGSやStanは実務でも利用されています。これらはモデルを記述する専用の言語を用いて直感的にモデルを組み立てることができます。またLispを拡張したChurchという言語はモデルを組み立てるのにホスト言語の機能がそのまま使えると言うメリットが有ります。またAnglicanやPyMC3はそれぞれClojureとPythonのライブラリとして提供されており既存の開発環境をそのまま使えるというメリットが有ります。Haskellを使って作られた言語としてはHakaruやBAli-Phyといったものがあります。

確率的プログラミング言語は新しい言語を作ることで確率変数を第一級オブジェクトとして使えるという利点があります。その結果、宣言が簡潔になったりifなどの文法と組み合わせて使うことができるようになります。ところでHaskellでは確率変数はモナドのインスタンスになることを見てきたと思います。この性質を使えば元の言語に手を加えることなくあたかも確率変数が第一級オブジェクトかのようにHaskellでも確率的プログラミングを扱うことができるようになるのではないでしょうか。

Haskellで実装してみる

前に作ったDistでは確率モデルを記述することができますが得られたデータから確率分布を推定する事はできませんでした。なのでここでは得られたデータを使って事後分布をサンプリングする機能を作っていきたいと思います。なおここでの話は Practical Probabilistic Programming with Monads を大いに参考にして書かれています。

今回作るDistは

• random-fuで定義されている確率変数を埋め込めるように
• データからサンプリングが出来るように

してみたいと思います。

{-# LANGUAGE GADTs #-}

type Prob = Double

data Dist a where
  Pure :: a -> Dist a
  Bind :: Dist b -> (b -> Dist a) -> Dist a
  Primitive :: RVar a -> Dist a
  Conditional :: (a -> Prob) -> Dist a -> Dist a

condition :: (a -> Prob) -> Dist a -> Dist a
condition = Conditional

前のDistとはぜんぜん違うものになってしまいました。それもそのはずDistはもはや直接確率分布を表すものではなくGADTｓを使った単なるDSLになってしまったのです。気持ちとしてはPureとBindはMonadのインスタンスにするために、Primitiveはrandom-fuのRVarを埋め込むために、Conditionalはデータから得られた条件を反映するために用意しています。これらのDSLに意味を持たせるにはインタプリタを実装する必要がありますが、その前に一旦Monadまでのインスタンスを定義してしまいましょう。

instance Functor Dist where
  fmap f d = d >>= (pure . f)

instance Applicative Dist where
  pure = Pure
  f <*> a = a >>= \x -> fmap ($x) f

instance Monad Dist where
  (>>=) = Bind

PureとBindはモナドになることを意識して用意しているのでMonadのインスタンスはすんなり作ることができます。MonadであればApplicativeとFunctorのインスタンスは自動的に出来上がりますね。
さてインタプリタですが、

instance Sampleable Dist IO a where
  sampleFrom _ (Pure x) = pure x
  sampleFrom s (Bind d f) = do
    x <- sampleFrom s d
    sampleFrom s (f x)
  sampleFrom s (Primitive d) = sampleFrom s d
  sampleFrom _ (Conditional _ _) = undefined

この様にrandom-fuのSampleableの実装に押し付ける形で作ります。これでDist aからIO aに変換できるようになるはずです。ここでConditionalの場合の返り値がundefinedになってて危険そうですが、sampleFromはConditionalを全て取り除かれたDistに対して適用されるという前提で話を進めていきます。

Conditionalが全て取り除かれた状態とはどういうものかというと与えられた条件に対してベイズ更新が全て終わった後の事後確率分布です。事後確率分布を求めるためにいよいよサンプリングの関数を作っていきましょう。

import qualified Data.Random.Distribution.Bernoulli as Random

bernoulli a = Primitive $ Random.bernoulli a

prior :: Dist a -> Dist (a, Prob)
prior (Conditional c d) = do
  (x,s) <- prior d
  return (x, s * c x)
prior (Bind d f) = do
  (x,s) <- prior d
  y <- f x
  return (y,s)
prior d = do
  x <- d
  return (x,1)

mh :: Int      -- burn-in 期間
   -> Int      -- サンプリング数
   -> Dist a   -- `Conditional`を含む事前分布
   -> Dist [a] -- 事後分布からサンプリングした点列上の確率分布
mh dc tc d = fmap (map fst . drop dc) $ proposal >>= iterate (dc + tc)
  where
    proposal = prior d
    iterate 0 _ = pure []
    iterate n (x,s) = do
      (y,r) <- proposal
      accept <- bernoulli $ min 1 (r / s)
      let next = if accept then (y,r) else (x,s)
      rest <- iterate (n-1) next
      return $ next:rest

mhはメトロポリスヘイスティング法を用いて事後分布を求める関数です。これは設定値を受け取ってConditionalを含む事前分布から事後分布からサンプリングした点列上の確率分布を求める関数になっています。返り値のDistにはConditionalは含まれませんので安心して結果を取り出すことができます。 priorはmhの中で提案分布として使用するために尤度を引き回しながら事前分布を求める関数です。

それではこれらを使って簡単なベイズ線形回帰を試してみましょう。

import qualified Data.Random as Random

normal a b = Primitive $ Random.normal a b

type Point = (Double, Double)
type Param = (Double, Double)

linear :: Dist Param
linear = do
  a <- normal 0 5
  b <- normal 0 5
  return (a,b)

point :: Point -> Dist Param -> Dist Param
point (x,y) = condition (\(a,b) -> pdf (Random.Normal (a*x + b) 1) y)

points :: [Point] -> Dist Param -> Dist Param
points ps d = foldl (flip point) d ps

trainingData :: IO [(Double, Double)]
trainingData =
  let points = [-5..5]
      equation = \x -> 2 * x + 1
      addNoise x = sample $ Random.Normal x 1
   in sequence . map (\x -> (,) x <$> addNoise (equation x)) $ points

main :: IO ()
main = do
  td <- trainingData

  putStrLn "Sampling..."
  xs <- sample $ mh 100 100000 (points td linear)

  putStrLn "Drawing..."
  r2AxisMain $ myaxis $ nub xs
    where
      myaxis :: [(Double, Double)] -> Axis B V2 Double
      myaxis mydata1 = r2Axis &~ do
        scatterPlot mydata1 $ key "data 1"

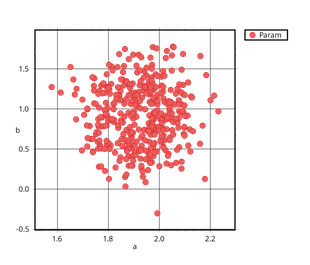
学習データとして $y = 2x + 1$ に標準正規分布に従うノイズを加えたものを使っています。グラフのプロットにはplotsというライブラリを使っています。

$ runhaskell Main.hs
Sampling...
Results:
a: 1.9233401839331328
b: 0.9046290119555563
Drawing...

プロットした図はこんな感じ。

まとめ

確率分布はモナドになり、それを使ってモデルの記述やパラメータの推定が直感的で簡潔に書けることを紹介してきました。本当は確率的プログラミングの型理論の話から量子コンピュータの話まで書きたかったけど知識も時間も足りずに挫折…。

この記事は第37回Haskellもくもく会@朝日ネットのもくもく時間を利用して書かれました。