初めに
とうとう研究室への立ち入りも禁止されてしまい,研究もなかなか進められないので,学部2年生のときに購入させられたけど講義では一度も触らなかったC言語を使ったプログラミングの教科書の演習問題を解いているのですが.
魔方陣を作れと言う問題に当たり,コードは書けたのですが,最近C言語に触らなさ過ぎてコードがとても汚くなってしまいました.
C++で書き直したかったので書き直したので,それのメモをと.
それと,魔方陣についての面白そうな文献をいくつか見つけたので,それのメモです.
今回の記事は完全に備忘録ですね.
具体的に書いた内容
魔方陣の作り方は幾つかあるようですが,大別すると
- 奇数次の場合
- 二重偶数(和訳に不安,英語だとdoubly even,4で割り切れる偶数のこと)次の場合
- 単偶数(英語だとsingly even,4で割ると2余る偶数のこと)次の場合
の3種類があるようですが,偶数次の場合は先の本でも飛ばしていたので,今回は奇数次だけの魔方陣を作ろうかと思います.
偶数次はゴールデンウィーク中に余力があれば.
更に問題を簡単にするために,以下の様な条件で魔方陣を作っていきます.
- ある奇数$n \in \{ x\in\mathbb{N}\ |\ x \equiv 1\ \mathrm{mod}\ 2 \} $に対し,$n$次の魔方陣に限る.
- 魔方陣に利用する数字は$\{ 0, 1, 2, \dots , n^{2} - 2, n^{2} - 1\}$の$n^{2}$個の自然数とする.
- 魔方陣が作れればよい(種類の全数探索などは行わない).
多分修士が書く内容じゃないですね,これ.
奇数次の魔方陣を作る(多分)最も簡単なアルゴリズム
アルゴリズム概要
今回利用したアルゴリズムは,Siamese methodとかDe la Loubère methodとか,ヒンズーの連続方式とか呼ばれているみたいですが,ソースまでは辿り着けませんでした.
詳細は記事の下の方にある参考文献を見ていただければよいかと思います.
家にいると,普段研究室からならアクセスできる論文にも行き着けなくて不便ですね.
- 魔方陣の次数$n \in \{ x\in\mathbb{N}\ |\ x \equiv 1\ \mathrm{mod}\ 2 \}$と自然数$x = 0$を用意する.
- サイズ$n \times n$の行列$M$を用意する.
- $\left( n, \mathrm{ceil}{\left(\dfrac{n}{2}\right) }\right)$を最初の位置$p \in I \times I$とする,但し$I := \{1, 2, \dots, n\}$.とする.
- 行列$M$の$p$に対応する要素を,$x$に更新する.
- $x$を1だけ増やす.
- 現在の位置$p = (u, v)$を$(u + 1, v + 1)$に更新する,但し$u + 1 \not \in I$や$v + 1 \not \in I$の場合($u + 1$や$v + 1$が$n$を越えてしまった場合には)$p$として$(u + 1 - n, v + 1 - n)$を採用する.
- 4~6の操作を$n$回繰り返す.
- 現在の位置$p = (u, v)$を$(u -2, v - 1)$に更新する,但し$u - 2 \not \in I$や$v - 1 \not \in I$の場合($u - 2$や$v - 1$が1を下回ってしまった場合には)$p$として$(u - 2 + n, v - 1 + n)$を採用する.
- 7~8の操作を$n$回繰り返す.
…分かり難いね.
具体例
最も簡単な$3 \times 3$の魔方陣を作っていきます.
流石に$1 \times 1$の魔方陣は簡単すぎますから.
余談ですが,$2 \times 2$の魔方陣は,同じ数を複数利用しないと作ることができないみたいですね.
先ずは空欄の魔方陣を用意します.そして一番下の行の,真ん中の列に0を入れます.

次にマス目の右下に,次に大きい数1を入れます.更にその右下のマス目に,2を…という風に,次数の3回繰り返していきます.
このときにマス目をはみ出してしまいます.

早速1が本来のマス目からはみ出していますね.
これを解決するために,1が元の魔方陣の中に入る様に,外側のマス目をスライドしてあげます.
スライドする際の移動量は次数の3マス分だけにします.
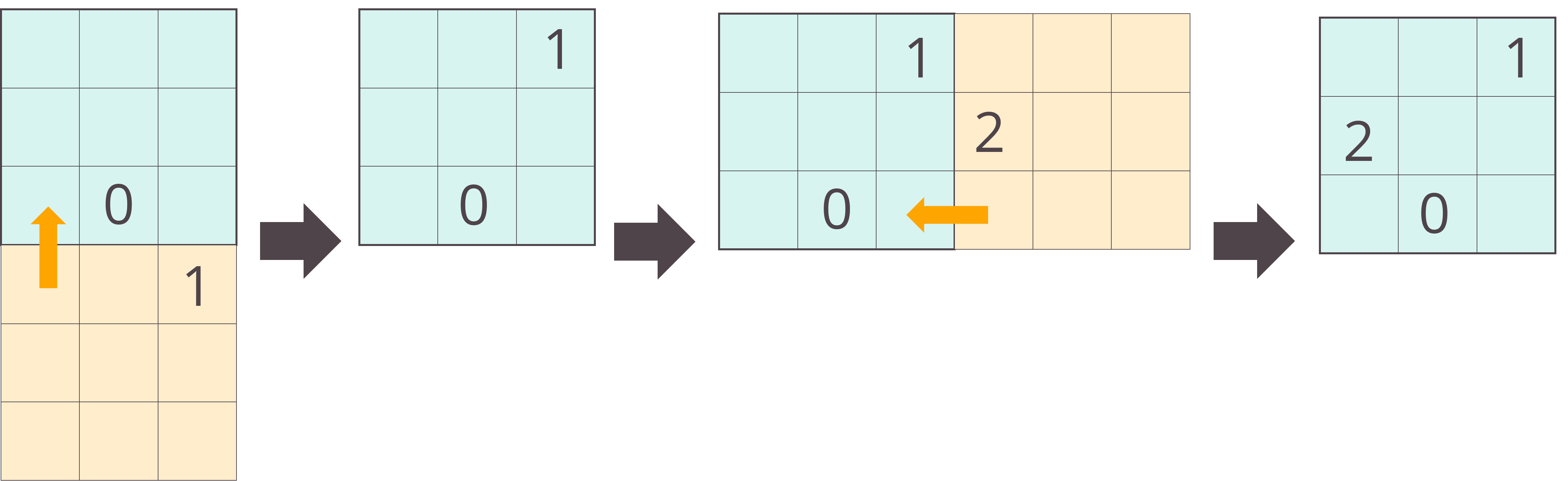
下図の橙色の部分を上に$n$マスずらします(この時に,1以外の数字がある部分も全部含めて同様にスライドさせます).

さて,次は2を処理します.
2は本来の魔方陣の右側に来てしまっていますので,左に次数の3マスだけずらします.

ここまでの流れが,上記のアルゴリズム概要の1~7の流れと一緒になります.
いや,じつは違うんだけど.
上記のアルゴリズム概要では, 1を埋める=>スライド=>2を埋める=>スライド という流れで,新しい数を埋めるたびにスライドを行っています.
アルゴリズム概要にこのように書いた理由は,実装はこっちの方が楽だからです.
商集合的な考え方に基づいてマス目を押し潰すことがベースなので,どちらの考え方も大差ない…筈,多分,きっと,maybe.
さて次の数を埋めたいところですが,2の右下に0が来てしまいました.
なのでこれ以上右下に進むことはできません.
そこで2の真上に3を置いてください.
そしてまた3回,右下に進んでスライドして.

5まで埋まりました.
また右下に進もうとすると3と同じマスにぶつかってしまうので,5の真上に6を埋めて、右下へ右下へ,そしてスライド.

魔方陣が完成しました,やったね.
因みに今回は埋める数を0から始めましたが,1から始めても問題ありません.
魔方陣中の数に同じ数を足そうが掛けようが,魔方陣になりますから.
実装
計算機環境
計算機環境は以下の通りです.
| OS | Windows 10 Home 1909 |
| CPU | Intel(R) Core(TM) i7-4510U プロセッサ |
| RAM | 8.00 [GB] |
| IDE | Microsoft Visual Studio 2019 Community 16.4.0 |
| コンパイラ | Microspft Visual C++ 14.24 |
コード
ソースコード全体はこちらからどうぞ.
cppファイル1つしかないけど.
とはいえ,難しいコードは何も書いていないです.
先ずは2次元配列を用意します.
今回は魔方陣の次数をキーボード入力にしたので,std::vectorを利用しました.
また魔方陣を埋める数に自然数を使っているので,std::uint32_tを利用しています.
vector<vector<uint32_t>> magic_square;
size_t square_size(0);
//Input Square Size
cout << "Input Magic Square Size: ";
cin >> square_size;
//Resize Square
magic_square.resize(square_size);
for(auto& it : magic_square){
it.resize(square_size, 0);
}
では奇数次の魔方陣を作っていきます.
template<typename T = uint32_t>
void createOddMagicSquare(vector<vector<T>>& square) noexcept(false){
const size_t square_size(square.size());
const T casted_size(static_cast<T>(square_size));
assert(square_size % 2 == 1);
size_t column_index(square_size - 1);
size_t row_index(square_size / 2);
T number(0);
for(size_t column_cnt(0); column_cnt != square_size; ++column_cnt){
for(size_t row_cnt(0); row_cnt != square_size; ++row_cnt){
//現在のマス目に数を埋める
square[column_index][row_index] = number;
++number;
//右下のマス目に移動
column_index = (column_index + 1) % casted_size;
row_index = (row_index + 1) % casted_size;
}
//最後に埋めたマスの真上のマスに移動
column_index = (column_index + casted_size - 2) % square_size;
row_index = (row_index + square_size - 1) % square_size;
}
return;
}
今更ですが,for文の比較は!=よりも<の方が良いのですかね,よく分かりません.
インデックス$p$の初期値ですが,上記のアルゴリズム概要では行列をつかって説明したので,$p$の各要素は$\{1, 2, \dots, n\}$に含まれていました.
多分皆様分かり切っていることとは思いますが,コードを書くときには,配列のインデックスは$\{0, 1, \dots, n - 1\}$となりますのでご注意.
コードでもそれが見て取れるかと思います.
例えば,こことか.
size_t column_index(square_size - 1);
size_t row_index(square_size / 2);
また数がマス目をはみ出したときの処理ですが,if文でごちゃごちゃ書くのが面倒だったので,剰余演算使っています.
例えばこの部分
column_index = (column_index + 1) % casted_size;
は,もう少し丁寧に書けば,
if(column_index + 1 > square_size){
column_index = column_index + 1 - casted_size;
}
else{
++column_index;
}
となります.
この部分
column_index = (column_index + casted_size - 2) % square_size;
については,column_indexが符号なし整数のことを考えると,素直に剰余演算使うのが楽そうです.
最後に結果をコンソールに表示させます.
見やすいようにフィールド幅を設定するといいかも.
//Calculation Maximum Number od Digits to Display
size_t max_digit = static_cast<size_t>(floor(log10(square_size * square_size) + 1));
cout << "Result:" << endl;
for(const auto& it_column : magic_square){
for(const auto& it_row : it_column){
cout << setw(max_digit + 1) << it_row << " ";
}
cout << endl;
}
下に$5 \times 5$の場合と$11 \times 11$の場合の結果を置いておきます.


終わりに
全体的に,ありきたりな内容になってしまいました.
色々と書きたいコードああるのですが,ありすぎて….
某無人島生活するゲームや某オープンワールドのゲーム買って時間が無いなんて,決してそんなことは.
参考文献
- 岡田 稔:『Cによるプログラミング演習』,初版,株式会社近代科学社,2016年,ISBN 978-4-7649-0220-6
- 東川 和夫:魔方陣の話,日本数学会 湘南数学セミナー・現代数学入門市民講座 講演録(数学通信11巻2号),2005年.
- 佐藤 昌子:魔方陣をつくる,芝浦工業大学 数理科学研究会 2015年度 芝浦祭 制作物,2015年.
魔方陣に関して個人的に気になった文献
- 石川 栄助:魔方陣の整数論的研究(其の一),岩手大学教育学部研究年報 1巻,pp. 7-16,1950年,.
- 石川 栄助:魔方陣の整数論的研究(其の二),岩手大學學藝部研究年報 2巻,pp. 3-6,1951年.
- 石川 栄助:魔方陣の整数論的研究(其の三),岩手大学学芸部研究年報 19巻,pp. 11-30,1961年.
- 漆原 煕:n進法を利用したn×n魔方陣の解法,徳島文理大学研究紀要 (57),pp. 199-235,1999年.
- 益冨 文男:数値表に等価な面積の円及び色彩の併記と効果:四魔方陣数値のグラフィック表現法例,電気情報通信学会 技術研究報告(信頼性研究会) 93(272),pp.61-66,1993年.
- 秋山 幸雄,弘畑 和秀:遺伝的アルゴリズムを用いた魔方陣の解法,茨城工業高等専門学校研究彙報 (47),pp.65-71,2012年.