Excelで24節気を概算する

JPLのApproximate Positions of the Planetsというページに、太陽系の惑星の位置をある程度の精度で計算するための軌道要素（ケプラー要素）や計算手順が記載されている。このページの情報をもとに、地球の位置を計算すれば24節気を計算することができるはずなので、2021年の24節気をエクセルを使って計算してみた。
このページによると、誤差は20秒角とのことなので、24節気を計算した場合の誤差は8分程度と考えられるが、どうだろうか？

ケプラー要素の説明

地球月重心を含む各惑星は楕円軌道に沿って移動していると考えられる。この章では楕円軌道のパラメータを紹介する。

$ $楕円の乗っている平面（公転面）を決定するのに 昇交点黄経(longitude of the ascending node) $\Omega$ と軌道傾斜角（inclination）$I$を使う。楕円軌道の形を決定するのに軌道長半径（semi-major axis）$a$ と 離心率（eccentricity） $e$ を使う。公転面上で、楕円の向きを決定するのに近点引数（argument of perihelion）$\omega$ を使う。
上記5つのパラメータで楕円軌道が決定できる。楕円軌道上の位置を表すために、さらに平均近点角（mean anomaly） $M$を使う。この記事では、これらの6変数を軌道要素と呼ぶ。太陽と惑星の質量が固定されていることを考慮すると、「位置と速度の6変数」と「軌道要素の6変数」は等価である。

ケプラー運動では楕円軌道を決定するための5つのパラメータは時刻によらず不変で、軌道は楕円である。しかし、各惑星は厳密にはケプラー運動をしおらず、あくまで「瞬時の軌道要素」⇔「瞬時の位置と速度」が相互に変換できるということである¹。実際の惑星の運動では、楕円軌道を決定するための5つのパラメータ（例えば近点引数）が常に変化しているということになる。

$\omega$と$M$は意味が少しわかりにくいので、代わりに近点黄経$\varpi$と平均黄経$L$を使うことがある。近点黄経は$\varpi=\Omega+\omega$、平均黄経は$L=\Omega+\omega+M$と定義する。$a,e,I,L,\varpi,\Omega$をケプラー要素と呼び、「ケプラー要素の6変数」は「軌道要素の6変数」や「位置と速度の6変数」と等価である。

24節気の説明

太陽の視黄経が0°、15°、などになる瞬間を春分、清明などと呼び、黄道1周360°に存在する24回をまとめて24節気と呼ぶ。それぞれの視黄経に対応する名称は規則的ではなく、次の表のようになっている²。

視黄経	+0	+15	+30	+45	+60	+75
0	春分	清明	穀雨	立夏	小満	芒種
90	夏至	小暑	大暑	立秋	処暑	白露
180	秋分	寒露	霜降	立冬	小雪	大雪
270	冬至	小寒	大寒	立春	雨水	啓蟄

「24節気を計算する」というのは、このように定められた春分や清明などの日時を求めることである。

24節気は、国立天文台で計算し、暦要項という文書で発表しているため24節気の日時を知りたい場合は、国立天文台から発表されている情報を参照してください。この記事の趣旨はそれをあえて自前でエクセルで数式を組んで計算してみた、ということである。

太陽は黄道を1年で1周するので1日あたり約1°進んでいる³。ということは1時間で2.5分角、1分で2.5秒角くらい進む。24節気を計算した際の誤差を検討する際に使うので、この関係を表にしておく。

角度	太陽が進むのにかかる時間
1°	1日
0.3°	7時間
1分角	24分
20秒角	8分
2.5秒角	1分
1秒角	24秒
42mas	1秒

Approximate Positions of the Planets の見方

このページではケプラー要素を使った惑星の位置の求め方が説明されている。
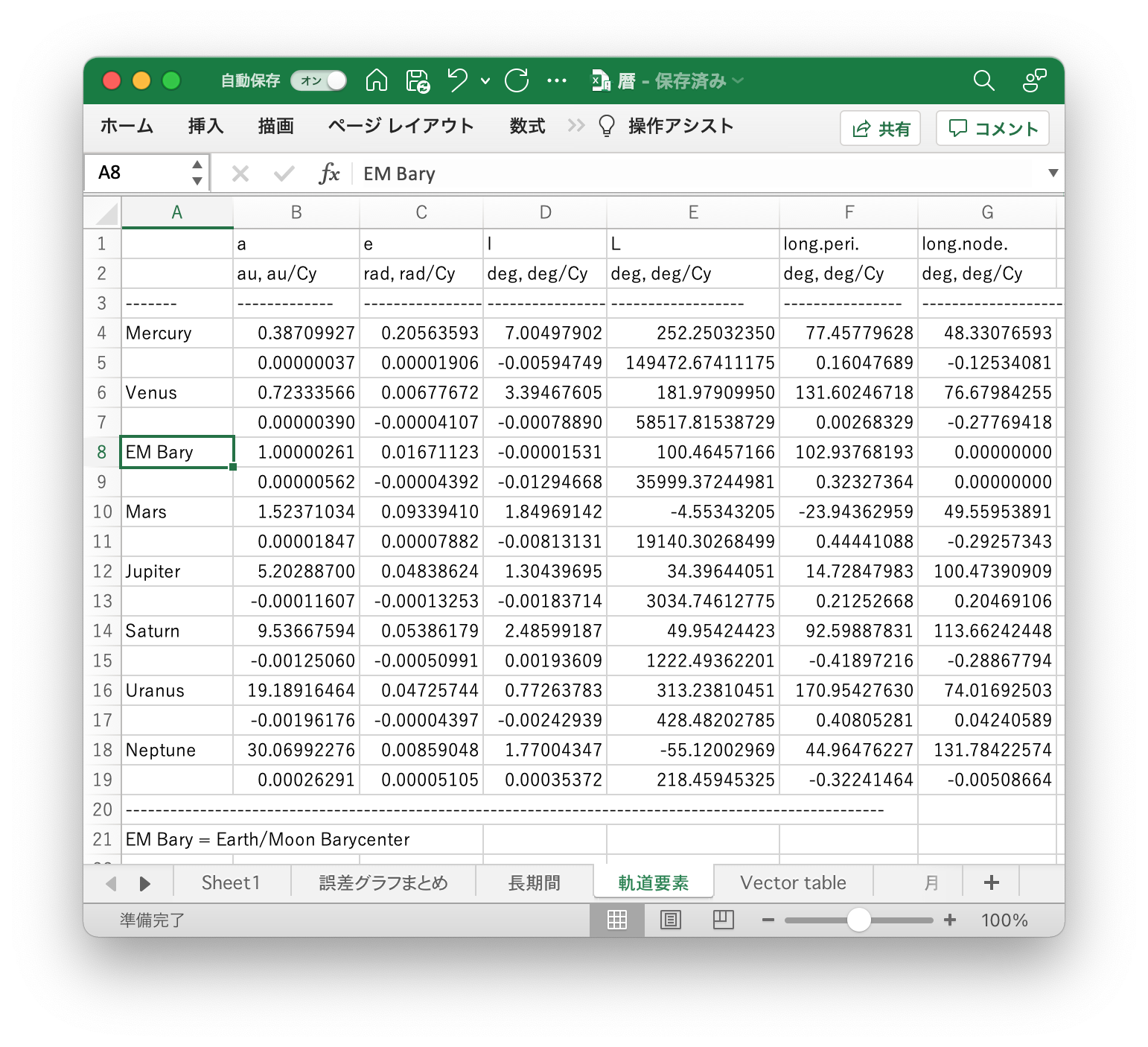
後半にTable 1、Table 2a、Table 2bの3つの数表がある。この表に出てくるEM Baryというのが地球月重心のことである。今回は、2021年の24節気を計算しようとしているので、Table 1を使うのが適切である。ページ上部の表によると、Table 1を使った場合の誤差は20秒角なので、24節気の計算誤差は8分程度と予想される⁴。

ユリウス日というのは紀元前の特定の日からの通算日数で、小数部分を使い時刻を表す。小数部分の使い方はエクセルのシリアル値と同様である。エクセルのシリアル値に2415018.125を足すと、ユリウス日になる。2415018.125というのは、2000年1月1日正午のユリウス日2451544.625と、エクセルのシリアル値36526.5⁵の差である⁶。

記載されているEM Baryのケプラー要素の数値について考察してみよう。

軌道要素	考察
軌道長半径	ほぼ1天文単位。1天文単位は、地球から太陽までの距離とほぼ等しくなるように定義されているため
離心率	0に近い値なので軌道は真円に近い楕円
軌道傾斜角	座標系の基準が地球のためほぼ0
昇交点黄経	座標系の基準が地球のためほぼ0
近点黄経	変化率が0.323°/世紀というのは、1周するのに約11万年かかるペース7
平均黄経	変化率が36000°/世紀に近いというのは、1世紀（＝100年）の間に地球が太陽を100周するから

それではさっそく、エクセルを使って計算してみよう。

エクセルでApproximate Positions of the Planetsの手順を実施

まずはApproximate Positions of the PlanetsのTable 1をエクセルに貼り付け、「区切り位置」機能で表にする。

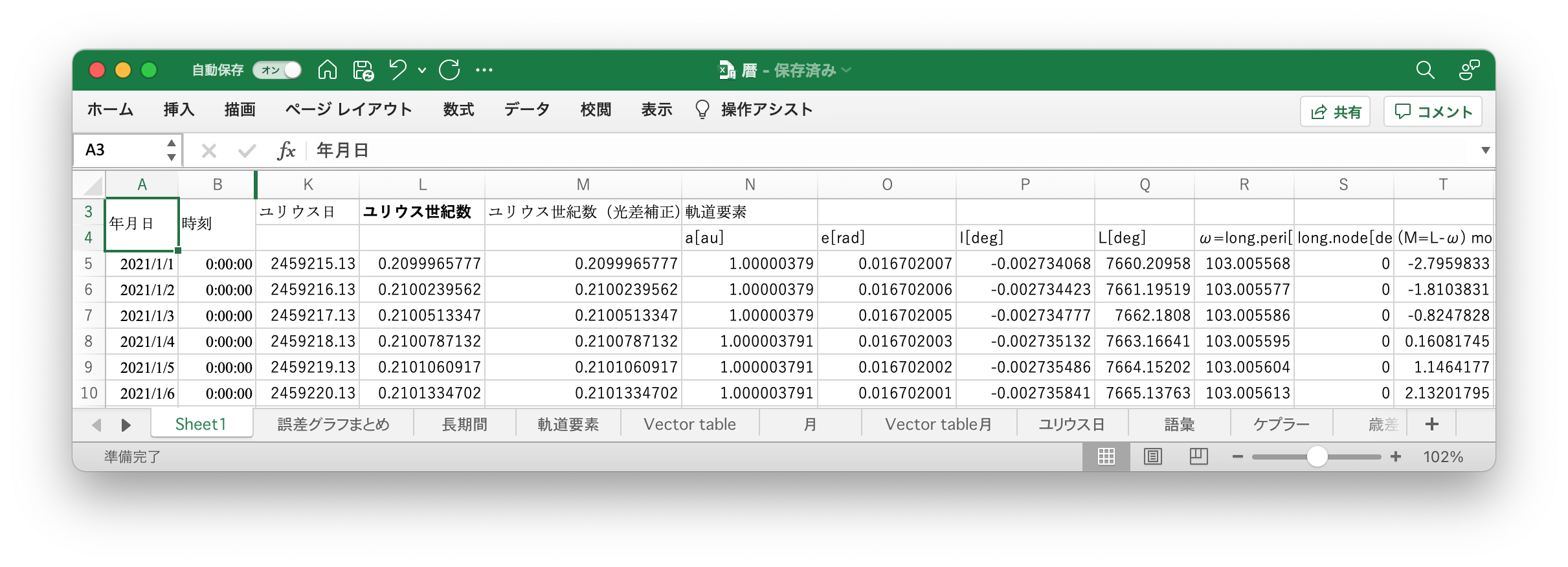
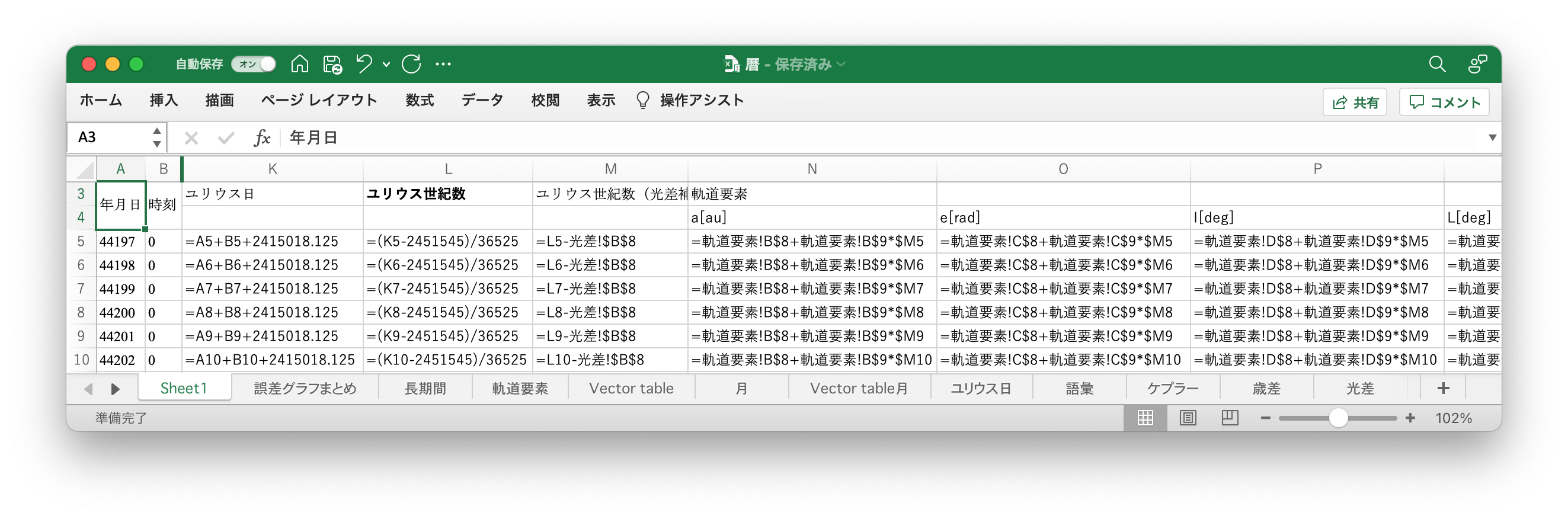
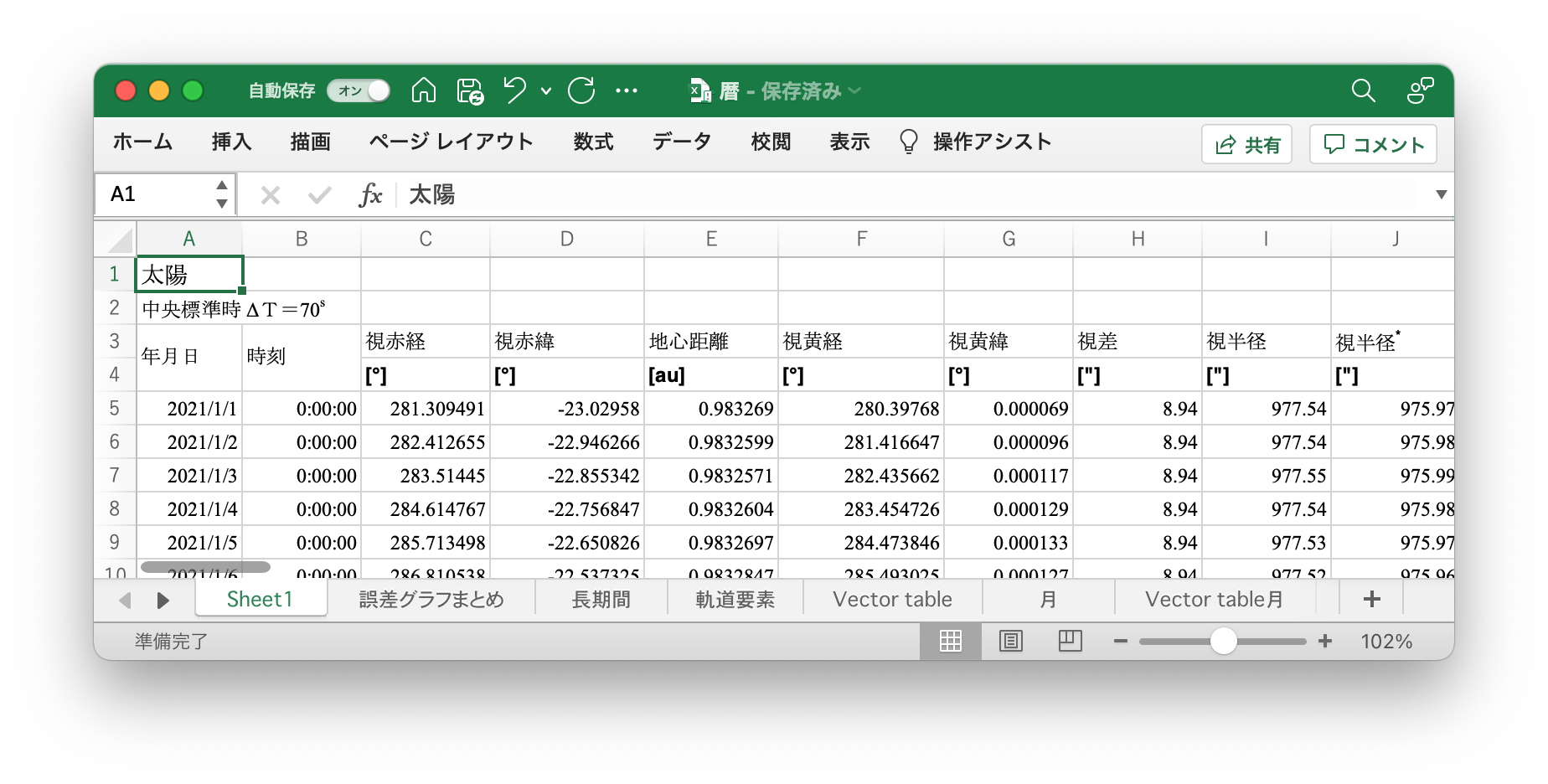
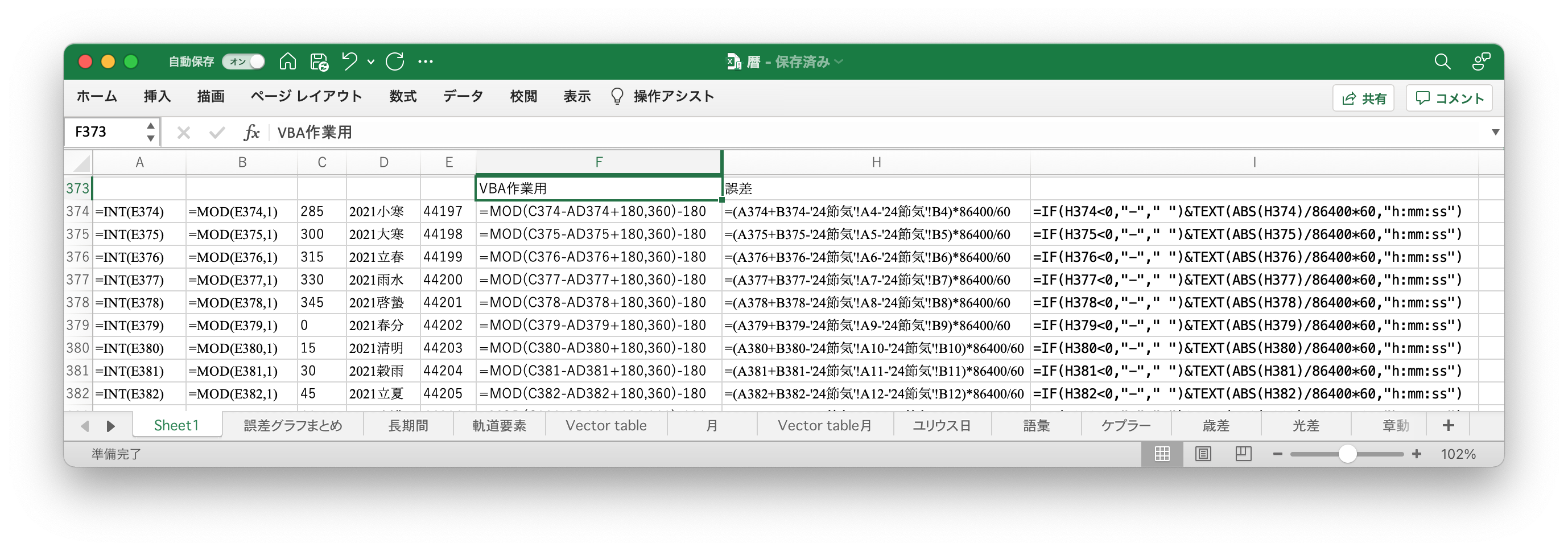
日時を入力するセルを作り、ユリウス日を計算し、Approximate Positions of the Planetsに記載されている数式を入力してユリウス世紀数とケプラー要素を計算する⁸。

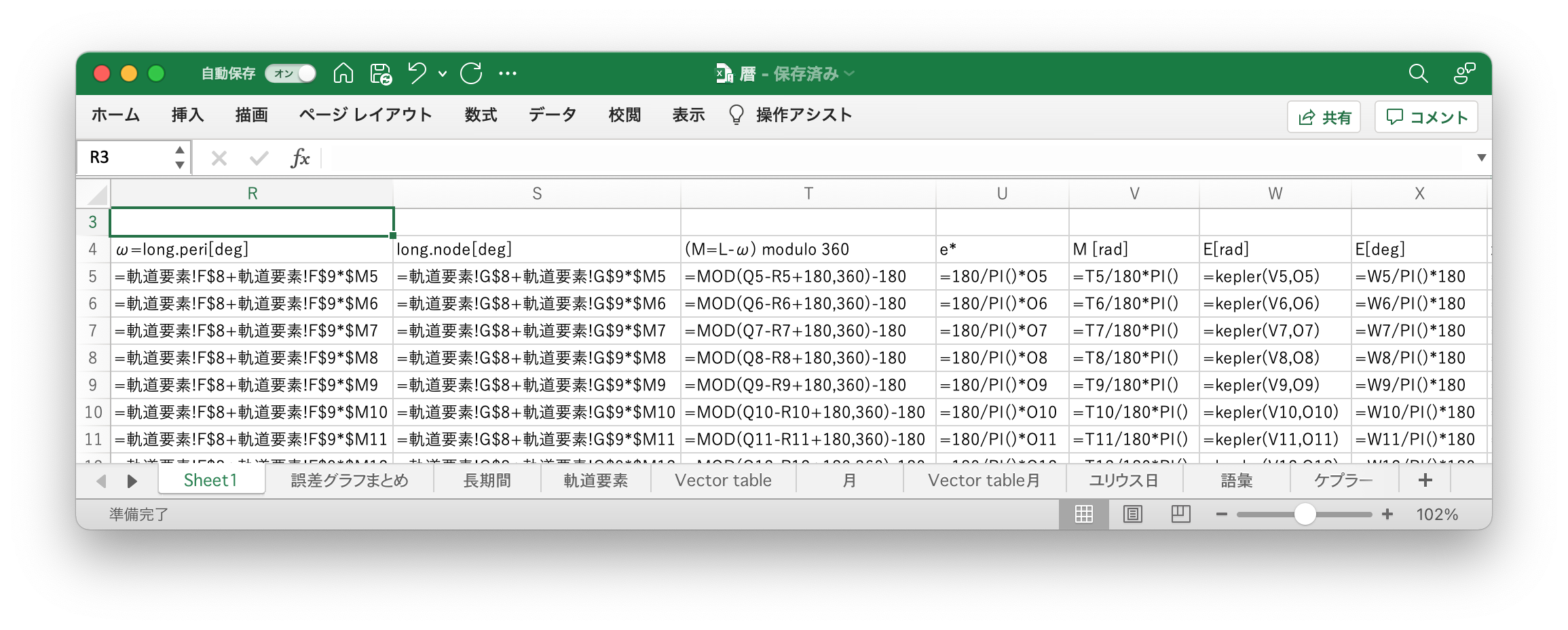
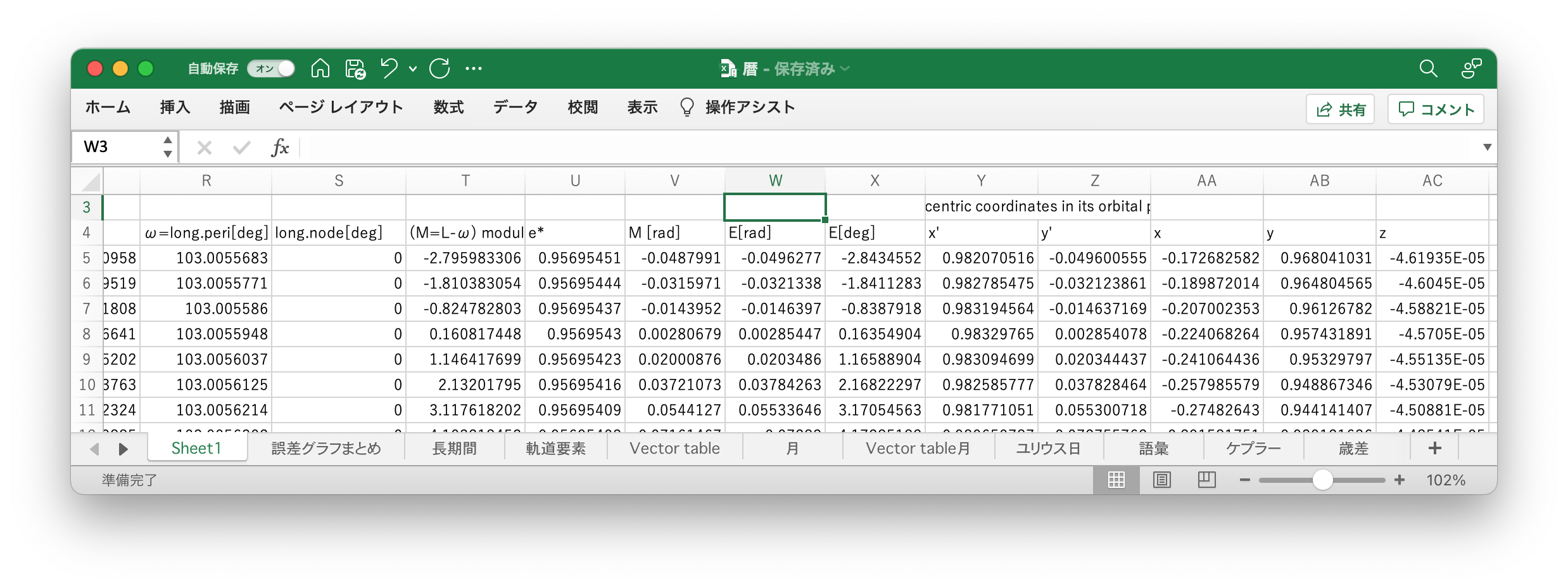
次にApproximate Positions of the Planetsの通りに平均近点角を計算する（画像のT列）。なおTable 1より、昇交点黄経は0°なので、そのことを利用して数式を簡略化している。角度の変数が-180と180の間になるようにするために、180ずらしてからMOD関数を適用し、180を引いている。

次は離心近点角（eccentric anomaly） $E$である。Approximate Positions of the Planetsに記載されているアルゴリズムを実行するユーザー定義関数は次の通りである⁹。この関数を使ってW列で離心近点角を求めている。なお、この関数は弧度法で処理するので、V列やX列で弧度法の変換を行なっている。

Function kepler(m, ecc)
    e = m - ecc * Sin(m)
    For Count = 1 To 10
        dm = m - e + ecc * Sin(e)
        e = e + dm / (1 - ecc * Cos(e))
    Next
    kepler = e
End Function

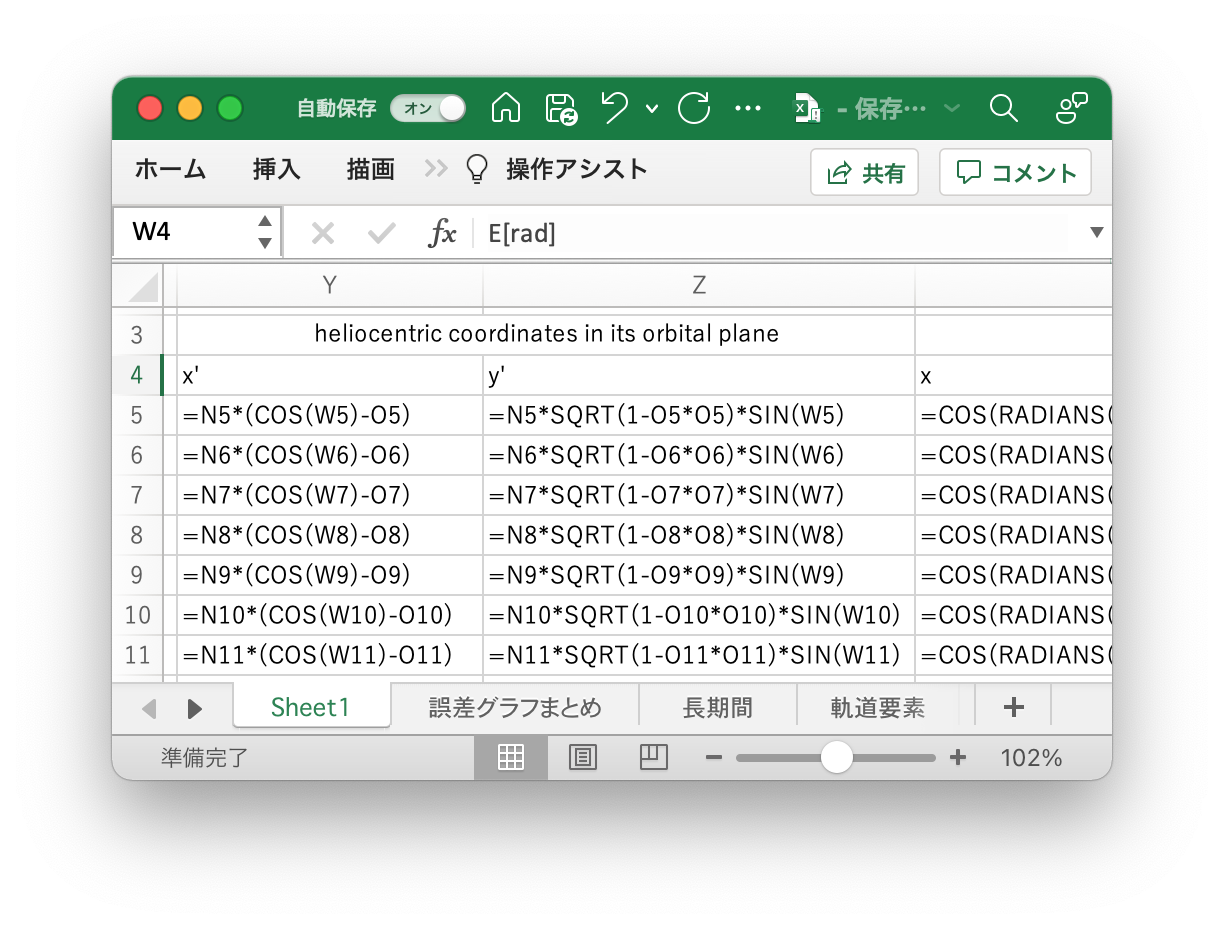
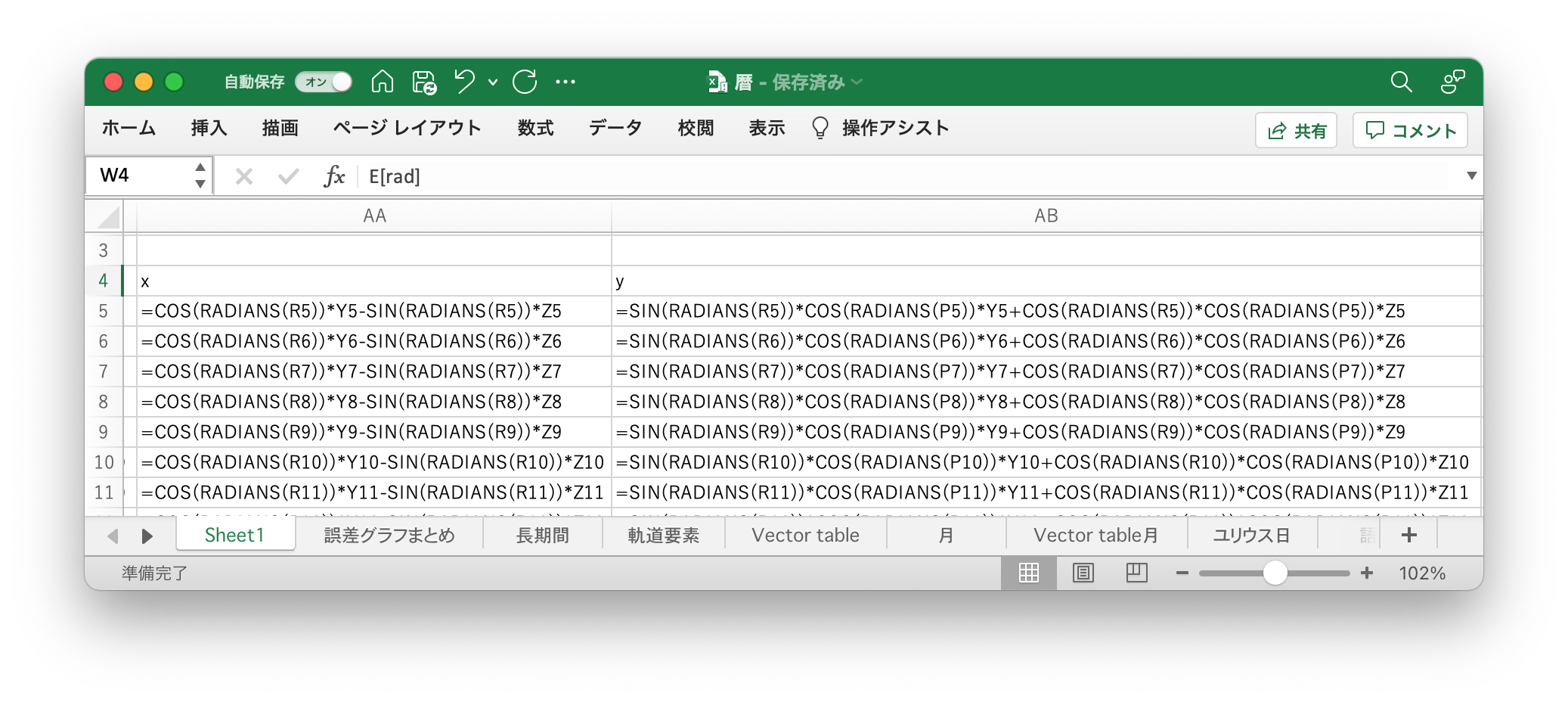
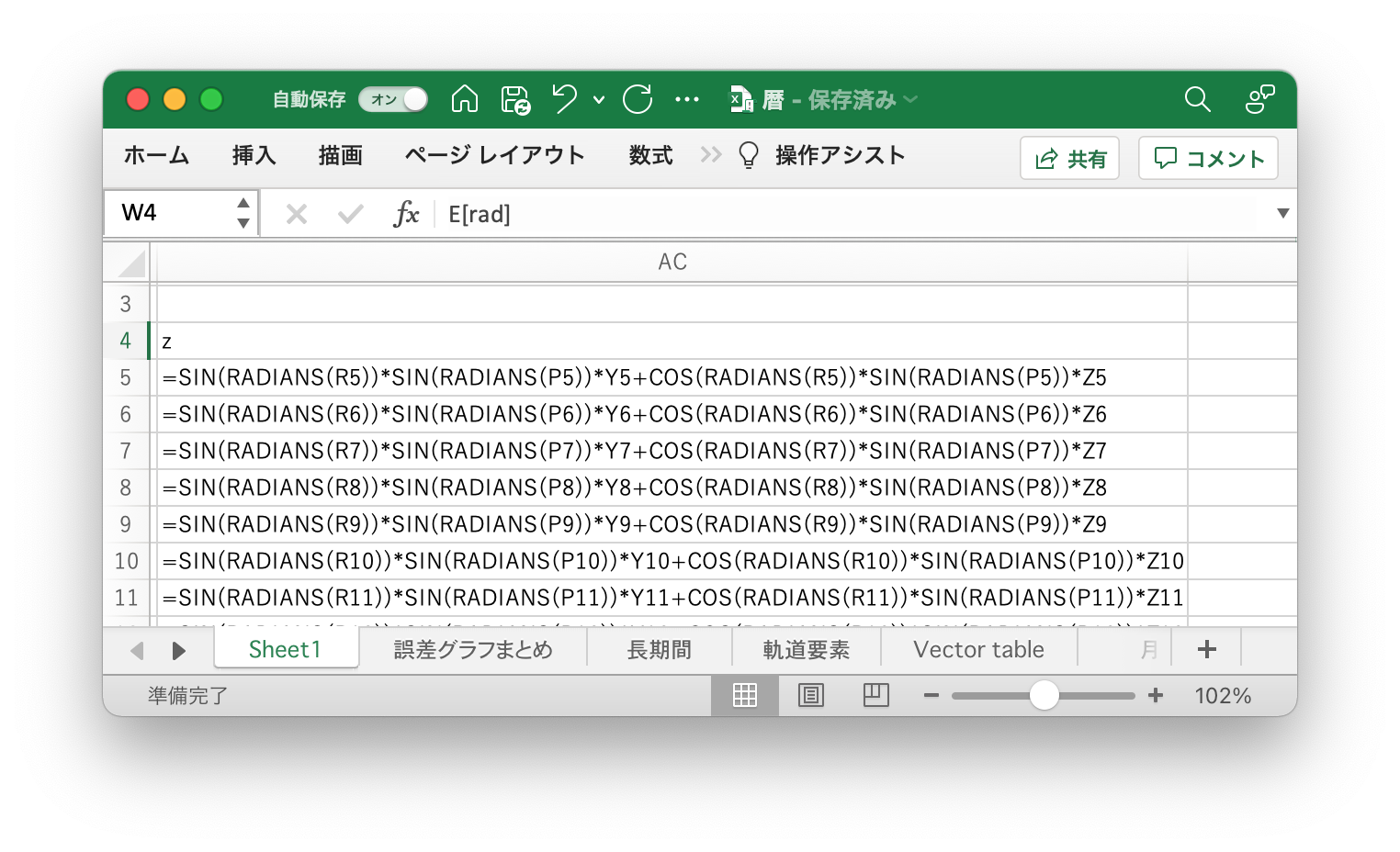
次に、Approximate Positions of the Planetsの数式で、公転面内での座標と3次元の直交座標を求める。ここでも、昇交点黄経が0°であることを用いて数式を簡略化している。

以上で、エクセルのAA〜AC列に太陽からみた地球の座標値が表示された。

24節気の計算

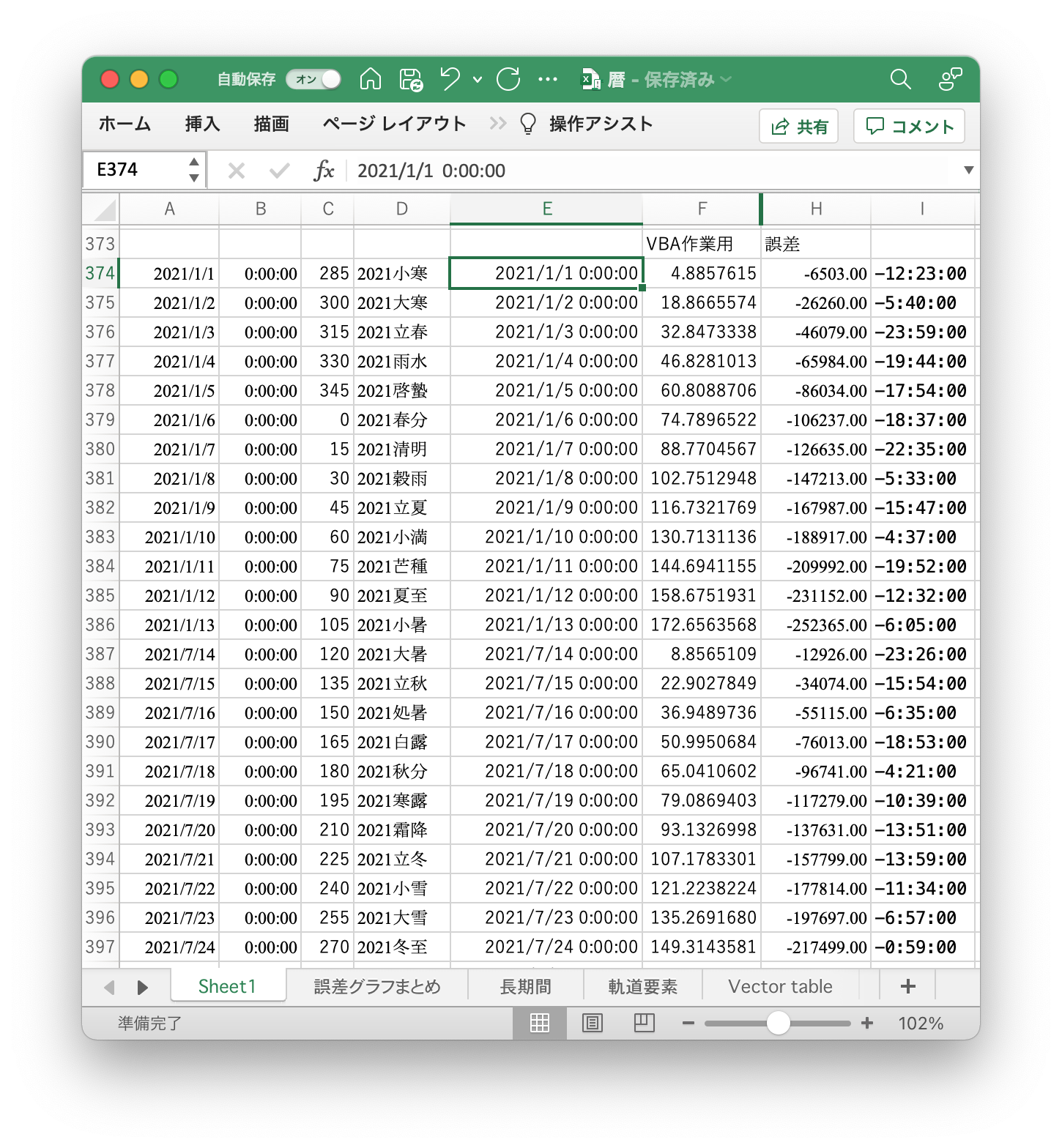
まず、視黄経の正解の値として、暦象年表の結果を貼り付けておく（下図のF列）。

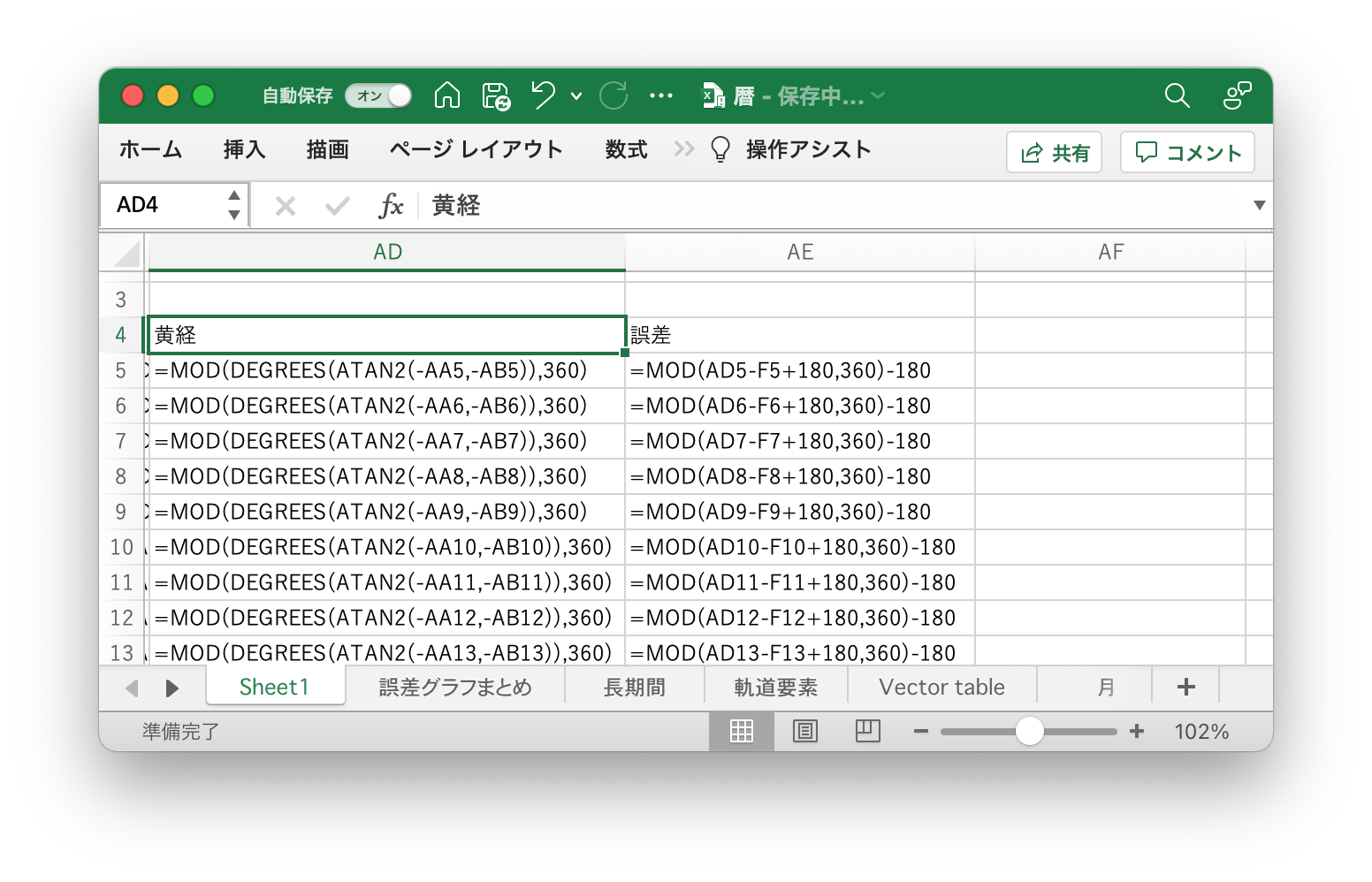
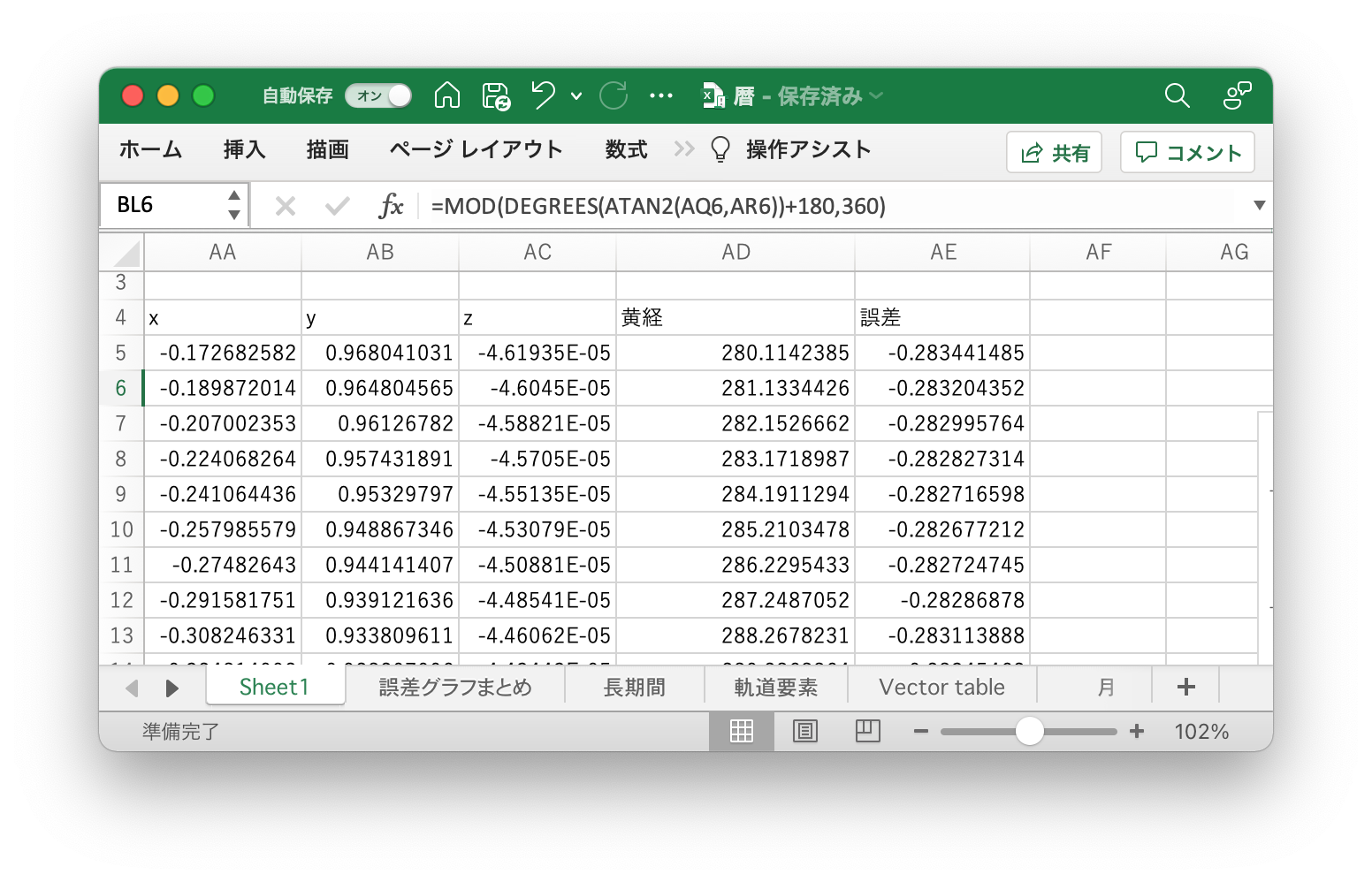
地球から見た座標にするためにAA〜AC列の座標値を-1倍し、ATAN2関数を使って黄経を求める。正解との誤差を計算する数式を入力する。

これによって黄経と誤差が表示される。

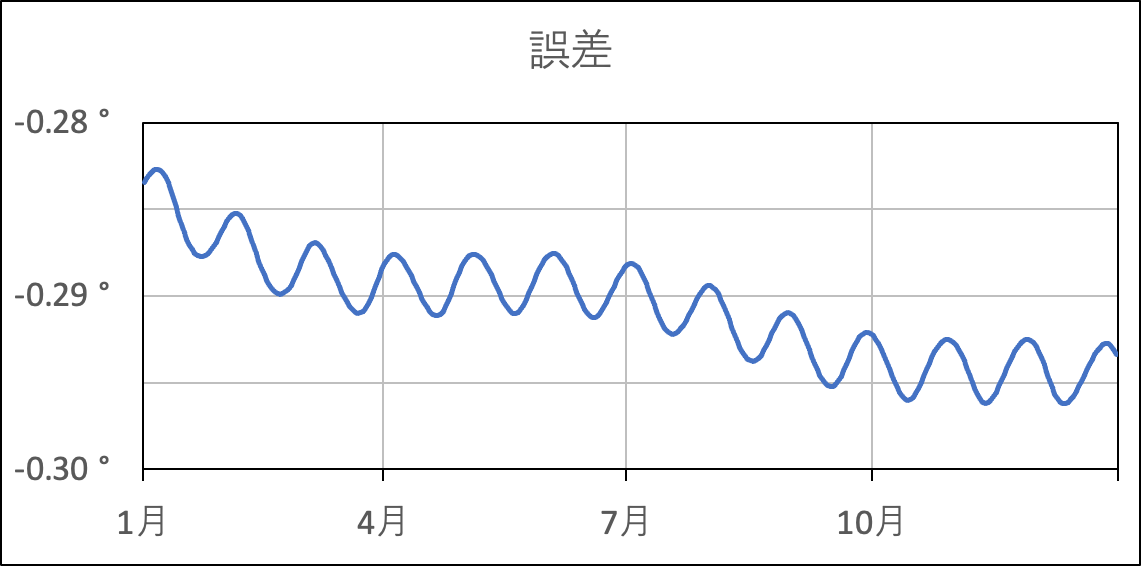
誤差をグラフにする。

今回計算した黄経は、正解の視黄経に比べて、0.29°程度、小さい値となっていたことがわかる。このまま24節気を計算したら、7時間程度、遅めの時間が求まるはずである。

では24節気を計算してみよう。
24節気の名前と対応する黄経を入力し、AD列の黄経との誤差を計算する数式を入力する。さらに暦象年表のページから、24節気の時刻の正解データを取得し貼り付けておき、正解との誤差を表示する数式を入力しておく。

24節気の計算には、次のマクロを使う。

Sub oikomi()
    For Count = 1 To 50
        If IsEmpty(ActiveCell) Then Exit For
        oikomi1
        ActiveCell.Offset(1, 0).Select
        DoEvents
    Next
End Sub
 
Sub oikomi1()
    oikomi_aux ActiveCell.Offset(0, 1), 1, 365
    oikomi_aux ActiveCell.Offset(0, 1), 1# / 24, 24
    oikomi_aux ActiveCell.Offset(0, 1), 1# / 24 / 60, 60
    oikomi_aux ActiveCell.Offset(0, 1), 1# / 24 / 60 / 60, 60
End Sub

Sub oikomi_aux(objcell, delta, max)
    For Count = 1 To max
            ActiveCell.Value = ActiveCell.Value + delta
            If objcell.Value < 0 Then Exit For
    Next
    ActiveCell.Value = ActiveCell.Value - delta
End Sub

このマクロを使うために、次のように初期値を入力しておく（E列）。

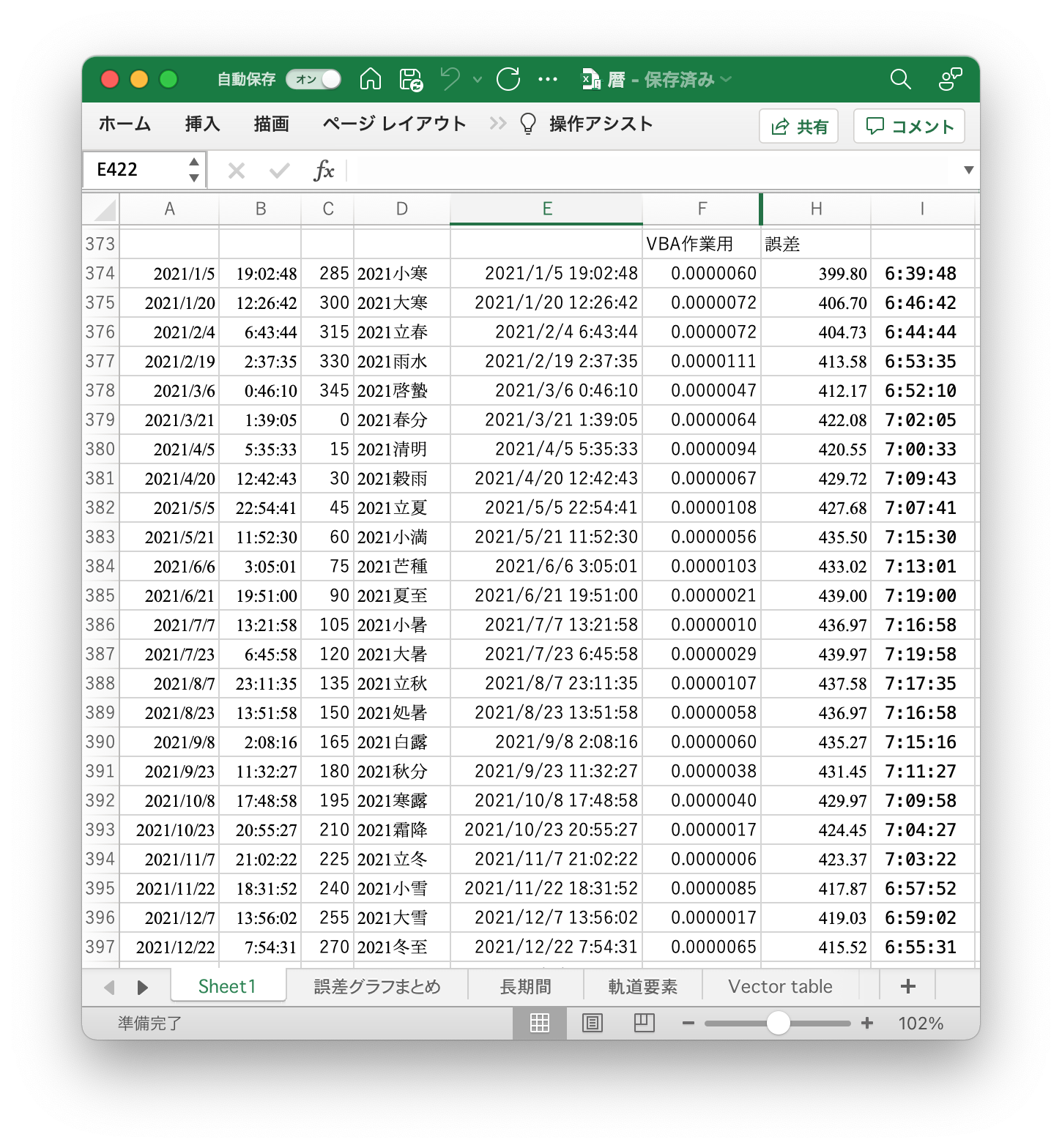
マクロを実行してしばらく待つと、計算結果が表示される。

以上で、24節気の計算をエクセルで行った結果を得られた。計算結果は正解と比較して7時間程度遅くなっている。

誤差の考察

誤差は8分程度になると予想していたが、7時間となってしまった。この誤差の最大の原因は歳差である。

今回の記事ではApproximate Positions of the Planetsのページに記載されている情報から計算してみたが、例えば、歳差を考慮するにはAstrodynamic Parametersに記載されている「general precession in longitude」の値を使えばよい。

実は、歳差、光差、地球月重心と地球の位置のずれ、章動を考慮して、精度が向上することを手元で確認できている。いつか続編記事を作りたい。

1. 数学で、2次の接触をする円というのがあるが、関係ない ↩

2. 部分的には規則的になっている。例えば、小寒・大寒の逆側が小暑、大暑となっている、など。 ↩

3. 赤経は0h〜24hで表記するが黄経なので°で表記する ↩

4. 赤経の誤差が20秒角とのことだが、黄経も同様と考えた ↩

5. エクセルの「1904年から計算する」という設定をしていない場合 ↩

6. この小数部分の説明。ユリウス日は世界時で特定の日の正午を基準にしているため、日本時間の正午は整数より0.375=9/24小さい値となる。一方、日本で使っているエクセルのシリアル値は日本の真夜中の0時を基準にしているため、正午の小数部分は0.5となる。 ↩

7. 金日点の移動参照 ↩

8. 画像には「光差補正」という列（M列）があるが、後で使うために用意したものであり、当面はL列と同じ値になるようにしてある。 ↩

9. ニュートン法によってケプラー方程式の解の近似値を求めている ↩