概要
競技プログラミングでJuliaを使おうというモチベーションのもと、初心者なのでJuliaのコーディングの練習も兼ねてセグメント木を実装してみました。来るAtCoderの言語アップデートに備えJulia v1.1.1で動くように実装したので、別バージョンだと動かないかもしれないです。
セグメント木とは?
一応、ざっくりと説明してみます。「もう知ってるよ」という方は実装のところまで飛ばしてもらっても大丈夫です。
セグメント木にもいろいろな種類があります。今回の記事で扱うセグメント木(一番メジャーだと思われる、本記事中でセグメント木というときには常にこのセグメント木を指す)は、**項の数$N$の数列が与えられたとき、ある区間$[L,R] \
\ (L \leq R)$についてのクエリを、区間の長さに関わらず、時間計算量$O(\log N)$で処理できるデータ構造です。また、初期化には$O(N)$、ある項を一つ更新するという操作に関しては$O(\log N)$かかります。**完全二分木の形をしているため、木という名前がついています。このままでは抽象的でわかりにくいので、一番基本的な和のセグメント木を例として見ていきましょう。
和のセグメント木
和のセグメント木は「区間$[L,R]$に含まれる項の和を取得する」というクエリの処理を$O(\log N)$で行えます。
これを愚直にやるとどうなるのでしょうか?
誰でも思いつく方法としては、1番目の項、2番目の項、…、7番目の項を足し合わせるという方法です。しかし、この方法では$O(R-L+1)$かかります。足す項の数だけ処理が必要です。このぐらい小さな数列で処理する分にはよいのですが、$N=100000, L=1, R=100000$の場合はどうなるでしょうか?仮にこのように長さが$10^5$オーダーの区間が$10^5$個与えられ、それぞれについて処理せよ、という課題が与えられたとすると、この方法ではとてつもなく時間がかかってしまいます。
しかし、セグメント木ではこれをうまくやり、$O(\log N)$で区間和を取得できます。$N=100000, L=1, R=100000$であれば、計算量が$10^5$から$17$程度まで落ち、5000倍も速くなります。1時間半かかっていた処理が1秒程度で終わってしまうぐらいの差です。
初期化
下図のようにまず空の完全二分木を作成します。最下層のノード数が数列の項数$N$に合うようにし、最下層に数列の値を入れます。完全二分木を作る際、最下層のノード数は常に$2^k$の形になるので$N$と合わない場合があります。そのときは、$N \leq 2^k$を満たす最小の自然数$k$を選び、余った部分を$0$で埋めれば大丈夫です。
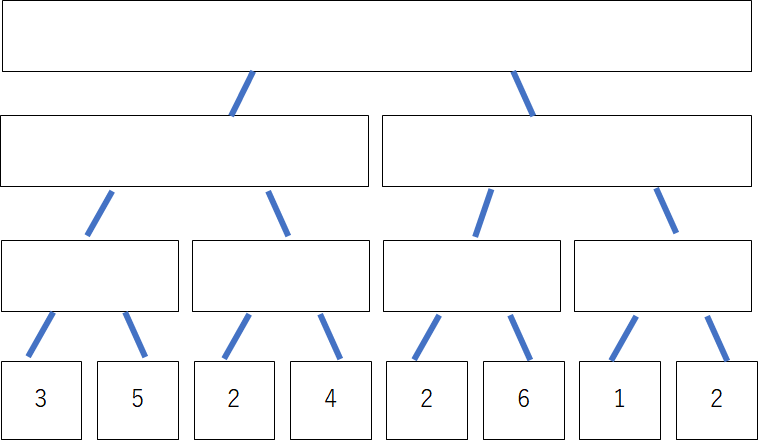
そして、最下層から、「親のノードに入る値は子のノードの和である」というルールで値を入れていきます。
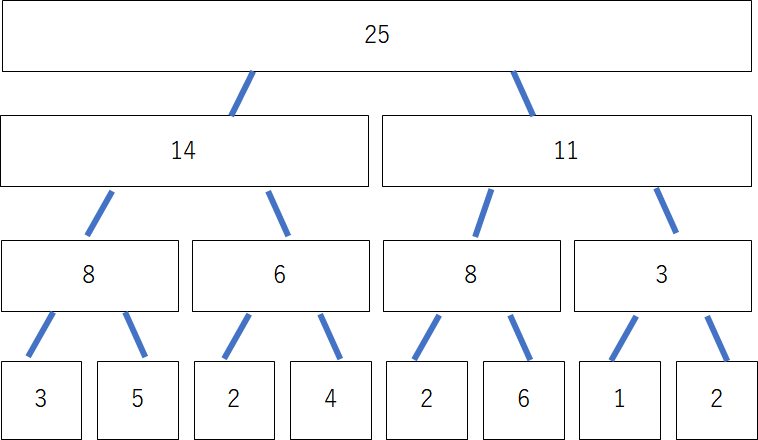
これで、初期化作業は終わりです。この各ノードはそれぞれが区間和を示しています。例えば一番上のノードは1番目から8番目までの和を表しており、二番目の階層の左のノードは1番目から4番目までの和を表しています。
区間取得
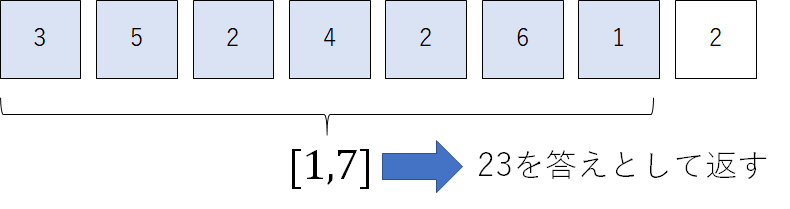
さて、いよいよ$O(\log N)$で区間和を取得します。さきほど挙げた$[1,7]$の区間についての和を取得するために以下のノードに注目します。
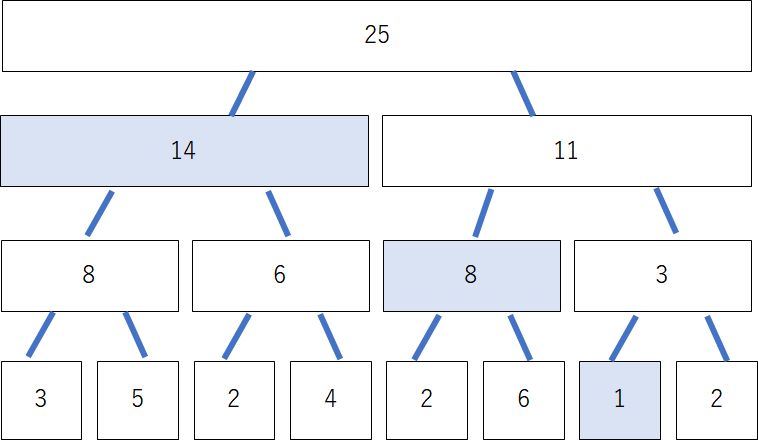
これらのノードを使えば、$[1,7]$を覆い尽くすことができます。実際に、これらの和をとってみると、23という答えを導出できます。ポイントとしては、各階層につきたかだか2つのノードまでしか注目しなくてよいということです。木の高さは$\log_2 N$程度であるので、その定数倍のノードだけしか見なくていいことになります。この工夫により、区間取得は$O(\log N)$で行うことができ、$N$が大きくなればなるほど絶大な威力を発揮します。
更新
また、セグメント木の機能で忘れてはならないのは更新です。これも$O(\log N)$でできます。やり方を下図に示します。
2番目の項を2から5に変えるとします。まずは、木の最下層の相当するノードの値を2から5に変えましょう。しかし、このままでは、他のノードの値と整合性がなくなってしまいます。
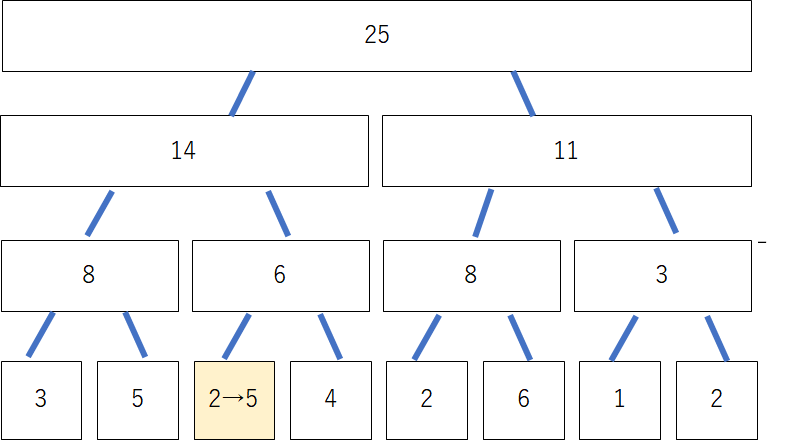
そこで、更新の影響を受ける親のノードを順番に変えていきます。一つ上の親は2が5に変わった影響で、6から9になります。この操作を下から上へと順番に行っていきます。
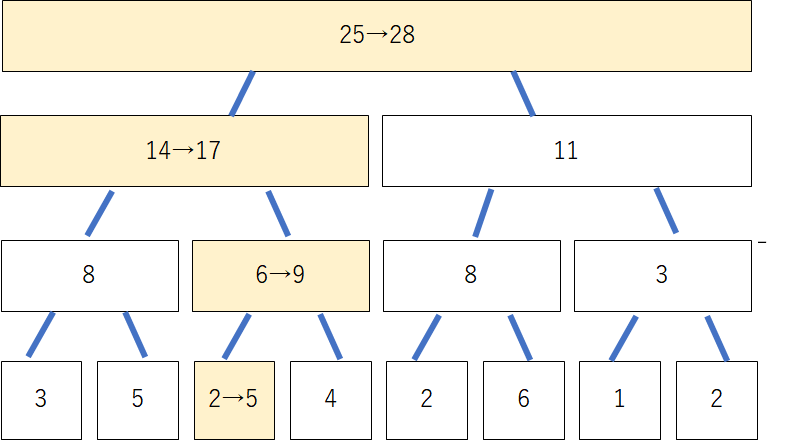
この操作もやはり、各階層につき一つのノードについて行えばよいので、$O(\log N)$での操作が可能となります。
累積和アルゴリズムとの比較
実は累積和アルゴリズムによっても区間和を高速で取得することが可能です。累積和アルゴリズムは$O(1)$で区間和を取得します。あれ?セグメント木よりも速い?そうです、区間和の取得だけなら累積和の方が速いです。しかし、累積和の問題点は更新に最悪の場合$O(N)$かかってしまうということです。すなわち、数列の値が何度も更新され、何度も区間和を求めたい、という動的な処理をするときにはセグメント木の方がよいパフォーマンスを発揮することが多いです。
また、配列は更新を$O(1)$ででき、区間和を求めるのに最悪$O(N)$かかるデータ構造とみなすことができます。累積和の逆ですね。配列は配列で、区間和を求めるのが遅いのがネックになるわけです。まとめると、更新と区間和の取得を何度もやる場合はどちらもそこそこ高速で行えるバランス型のセグメント木が最適です。
セグメント木の適用範囲 - モノイド
和のセグメント木を見てきましたが、セグメント木には和以外の演算も適用可能です。具体的には、モノイドという代数構造を持つような集合とその演算について、セグメント木を作ることができます。モノイドはある集合と演算の組で、結合法則が成り立ち、単位元が集合中に存在することが保証されているものです。例えば、整数(正確にはそれに適宜単位元を付加したもの)は$+$の他に$\min$や$\max$、$xor$によってもモノイドになります。それぞれ、単位元は$0,∞,-∞,0$です。すなわち、ある区間の最小値や最大値などを求めるクエリにも対応できます。アルゴリズムとしては、前述の足し算の部分を全てそれぞれの演算に変え、$0$の部分をそれぞれの単位元に変えればいいだけです。
累積和アルゴリズムを同じように拡張しても、実は群という、より条件の厳しい代数系についてしか適用できません。整数にそれぞれの単位元を付加した集合は$\min$や$\max$で群になりません。逆にモノイドというのは非常に緩い縛りなので、セグメント木は非常に応用の利くデータ構造となっています。
Juliaでの実装
ではいよいよ、Juliaで実装していきます。
参考にしたページのリンクを貼ります。
The Julia Language - 型 複合型の項を参照
DataStructure.jl 実際にJuliaでデータ構造を実装しているコードとして参考にしました
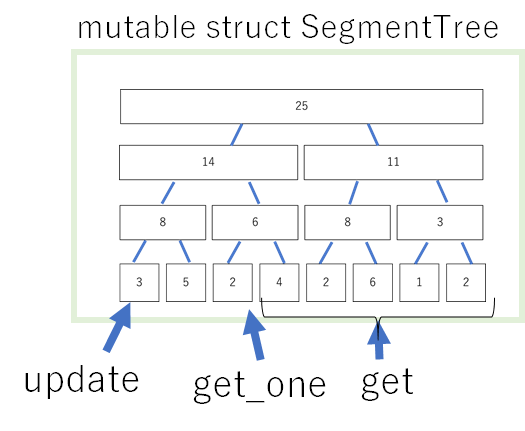
Juliaでデータ構造を実装するときには、mutable structを使い、データ構造が保持するデータの集まりを構造体として定義します。そして、データ構造で行いたい主要な操作を、その構造体を引数とする構造体外部の関数によって実装します。これはOOPが広まった今では少し珍しいのではないでしょうか。しかし、Juliaの特徴である多重ディスパッチ(複数の同名関数の中から引数の組み合わせにより最適な関数を呼び出す)を考えると、データ構造の構造体を引数とすることに合理性があります。
具体的に今回のSegmentTreeに関しては、mutable struct SegmentTreeを定義し(このコンストラクタで初期化も行う)、これを操作する関数、update(指定された項を指定された値に変える)、get_one(指定された項を取得する)、get(指定された区間に関してクエリを処理し、実行する)といった関数を外側で定義して実装します。
長くなってきたので続きはまた後日あげることにします。浅学非才ゆえ誤りも多いと思いますが、何かご指摘があればコメントをいただけると幸いです。