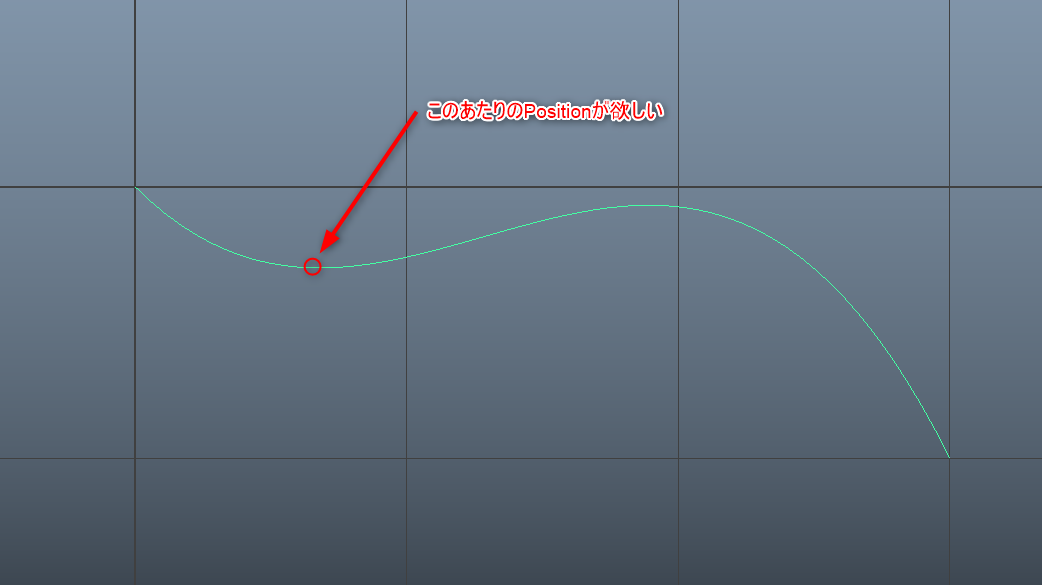
mayaでカーブの特定の箇所のPositionの情報を取ろうとしたら、control vertexのPositionは取れるけど特定の場所のPositionを取得するようなコマンドがない!
(よく探してないので実際はコマンドあるかもですが…)
じゃあカーブを1から計算してPositionを割り出そう!というお話です。
はじめに
mayaのCVCurveToolで作られるカーブは種類で言うとB-スプライン曲線になります。
wikipediaによるとB-スプライン曲線とは、与えられた複数の制御点とノットベクトルから定義される滑らかな曲線だそうです。
複数の制御点=control vertexなのであとはノットベクトルが分かれば計算できそうです。
ノットベクトルとは
ノットベクトルは、制御点がNURBS曲線のどこにどのように影響を与えるかを決定するパラメータの値(ノット)の列です。ノットの数は常に制御点の数+曲線の次数+1に等しくなります。
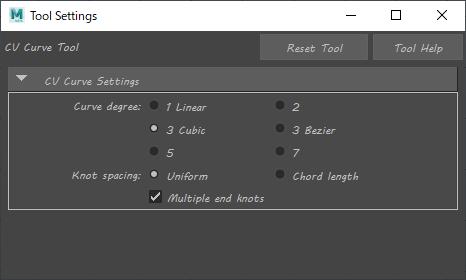
仮にmayaのデフォルトのままで曲線の次数(CurveDegree)を3、制御点(control vertex)を最小で4とするとノットの数は8となります。
pythonで計算
計算にはnumpyとscipyを使用します。mayaへの導入の仕方は説明してくれているサイトがけっこうあるので割愛します。
下記がコードになります。
import numpy as np
from scipy import interpolate
import maya.cmds as cmds
ctr = np.array([(0, 0), (1, 1), (2, -1), (3, 1), ])
x = ctr[:, 0]
y = ctr[:, 1]
l = len(x)
t = np.linspace(0, 1, l - 2, endpoint=True)
t = np.append([0, 0, 0], t)
t = np.append(t, [1, 1, 1])
tck = [t, [x, y], 3]
sample = np.linspace(0, 1, (max(l * 2, 70)), endpoint=True)
out = interpolate.splev(sample, tck)
for x, y in zip(out[0], out[1]):
cmds.spaceLocator()
cmds.move( x, y, 0 )
cmds.scale( 0.05,0.05,0.05)
(0, 0), (1, 1), (2, -1), (3, 1)が制御点になります。
それをその次の行でx,yに分けています。
ctr = np.array([(0, 0), (1, 1), (2, -1), (3, 1), ])
x = ctr[:, 0]
y = ctr[:, 1]
tがノットベクトルになります。
tの先頭に[0, 0, 0]と末尾に[1, 1, 1]に追加しています。このように複数のノットに対して、同一の値を与えることで曲線が制御点の上を通るようになりカーブの始点と終点の制御点が一致するようなります。
l = len(x)
t = np.linspace(0, 1, l - 2, endpoint=True)
t = np.append([0, 0, 0], t)
t = np.append(t, [1, 1, 1])
scipyのsplevという関数を使用するのでそれ用にデータを整形します。
・ノットベクトル
・制御点(x,y)
・曲線の次数
上記を一つにまとめます。
tck = [t, [x, y], 3]
sample はどれくらいの間隔でPositionを取得するかの値になります。70のところを大きくすると取得できるカーブが滑らかに、小さくするとカクカクになります。
interpolate.splev(sample, tck)でカーブを出力してoutに格納しています。
sample = np.linspace(0, 1, (max(l * 2, 70)), endpoint=True)
out = interpolate.splev(sample, tck)
計算としてはここまでですがせっかくなので、maya上に表示してみます。
取得したPositionの所にLocatorを配置していきます。
for x, y in zip(out[0], out[1]):
cmds.spaceLocator()
cmds.move( x, y, 0 )
cmds.scale( 0.05,0.05,0.05)
表示されました!mayaのカーブの位置と一致しているのも確認できました。

おわりに
今回は実験として平面空間でやりましたが、立体空間でも同じようにできるかと思います。
あまり応用が利く感じではないですが、カーブの仕組みを理解しておくと色々役に立つので参考になれば幸いです。