X Window SystemのライブラリXlibを使って疑似3Dのレーシングゲームを作った話

まえがき

某大学の授業ではXWindowSystemのライブラリXlibを利用した制作課題があります。ちなみにXlibとは、1985年に登場したUnix系OSのGUIに利用されているライブラリです。
つまりXlibは古のGUIライブラリであり、決してUnityのような高機能ゲームエンジンなどではないため、最低限の機能しか備わっていないと感じました。
このXlibを利用して2週間ほどで疑似3Dのレーシングゲームを制作したので、紹介します。

なお、コードはGitHubで公開しています。すぐ遊ぶこともできます。
https://github.com/levyxx/SpellRacing

もし同じ大学でこの授業を受けていれば、参考にするのは歓迎ですが決してコピペなどはしないようにお願いします。

完成したゲームの概要

SpellRacingというゲームを制作しました。名前通り魔法×レースがテーマのゲームです。見た目はこんな感じです。

マップは完全ランダム生成(距離が極端に短かったり長い場合の補正あり)です。
魔法については、１マスしか離れていない奥のフィールドにワープすることができます。(左下に表示されているミニマップを見ると分かりやすいです。)これが最も重要なゲームの要素で、マップはランダム生成なので左下のマップを見ながら3回まで使えるワープをどこで使えば最短でゴールに辿り着けるか考える必要があります。
他にも風加速、回転、たまに降ってくる酸性雨を防ぐシールドなどの魔法がありますが、大体どんな魔法か分かると思うので割愛します。

使用したXlibの機能

使用した機能を列挙すると、こんな感じになります。

・テキストの表示
・ドットの描画
・描画する色の変更
・キー入力(イベント)の受け付け
・ダブルバッファリング

これぐらいです。あとは線の描画なんかもありますが、これはドットの描画の拡張にすぎないので上の5つの機能ぐらいしか使ってません。まあ、少ないですね。
画像の出力とかもできたりしますが今回は使用していません。

ちなみにダブルバッファリングとは画面のチラつきを解消する技術です。
下の話は少し脱線しているので飛ばしても大丈夫です。
簡単に原理を説明します。まず前提として、ゲームはペラペラ漫画のように何枚もの画面を高速で切り替えて表示することで、あたかもゲーム画面が動いているように見えるようになっています。
ですが、1枚の紙に書いたり表示したりを繰り返していてはその間の画面も表示されてチカチカしてしまいますね。
そこで、2枚の画面を用意します。片方の画面をプレイヤーに表示する画面、もう片方の画面は次に移す画面を描画する画面とします。プレイヤーに表示していない方の画面の描画が終わればその画面をプレイヤーに表示します。このとき、先ほどプレイヤーに表示していた画面は描画用の画面に切り替わります。これを繰り返せば無駄な描画をプレイヤーに表示しないのでチラつきが解消されるというわけです。

実装方法

大まかな実装

とりあえず大まかな実装方法を説明してから、ランダムマップ生成と疑似3Dの実装についてあとから詳しく説明します。

２次元配列でマップを表現します。穴掘り法とBFS(幅優先探索)を利用してランダムな一方通行のマップを生成することができます。(後述)

また、プレイヤーの位置を座標で管理します。また、視点の方向を角度で管理します。

現在のプレイヤーの位置と視点から、実際に画面を描画します。このときに擬似3Dとなるようにうまく計算が必要です(後述)

プレイヤーの車体はドットの描画で表現しています。また、ドリフト時には回転行列を用いて全てのドットを回転して車体全体を回転させています。(後述)

なお、ドリフトや魔法、速度の変更など、他にも挙げ始めたらキリがないですが、大体の機能は容易に実装が可能なので割愛します。

車体の回転

まず、車体をどのように描画しているかと言うと、以下の手順を踏んでいます。

1. ドット絵を書く
2. ドット絵を色ごとに数字分けしてくれるサイトからcsvファイルで抽出する
3. csvを配列形式に書き直させる
4. この配列に従って各点にドットを打つ

めんどくさいですね。画像表示するライブラリもありますが最小限の機能で制作したいという謎の意地です。
さて、ドリフト時に車体を回転させたいので、回転行列を用いて車体を表すすべての点を回転させます。
ここで少しだけ回転行列について説明します。
点$(x,y)$を原点中心に$\theta$だけ回転させた点を$(x',y')$とすると、この点は以下のように計算できます。

\begin{bmatrix}
x'\\
y'
\end{bmatrix}
=
\begin{bmatrix}
    \cos{\theta} & -\sin{\theta} \\
    \sin{\theta} & \cos{\theta}
\end{bmatrix}
\begin{bmatrix}
    x\\
    y
\end{bmatrix}

上式で利用した2×2行列こそが(2次元の場合の)回転行列です。
また、平行移動を利用すれば回転の中心も任意に決定できます。

この式を用いれば、例えば車体を左に傾けたければ、回転の中心を車体の左下とかに設定して車体を表す全ての点を$\theta$だけ回転すれば下の画像のように車体を傾けられます。

回転行列はこのようなゲームプログラミングで頻出なので使いこなせると便利です。過去にDXライブラリで東方弾幕風を制作したこともあるのですが、そのときも弾幕の軌道を計算するときなど、回転行列を多用しました。

ランダムマップ生成

大まかな流れとしては、以下のようにマップを生成しています。このとき、マップは一方通行になるように生成されます。

1. 穴掘り法を用いてランダムな迷路を生成する
2. BFSを用いてスタートから各マスまでの最短経路を計算する
3. ゴールからスタートに、2.で計算した最短経路の数字が1ずつ減るように遡ってそれをコースとして採用する

1.から説明していきます。穴掘り法とはランダムな迷路を生成するアルゴリズムです。以下、2次元配列上に迷路を構成すると考えてください。まずは迷路のスタートとゴールのマスを設定します。次に、スタートのマスからランダムに上下左右を選び、今いるマスから2マス先が道でなければ、２マス進んで道にします。これを全てのマスから道が作れなくなるまで繰り返します。(再帰関数で実装できます。)
このようなアルゴリズムによってランダムな迷路を生成することができました。↓イメージ図

しかし、迷路がコースというのはレーシングゲームとして適切ではないかなと思ったので一方通行のコースにします。まず、BFSというアルゴリズムを使ってスタートから各マスへの最短距離を計算します。BFSのイメージとしては、以下のような感じです。

スタートから1マスで行けるマスを全て探索して距離1とする。→スタートから距離1のマスから1マスで行けるまだ到達していないマスを全て探索して距離2とする→$\cdots$→スタートから距離$k$のマスから1マスで行けるまだ到達していないマスを全て探索して距離$k+1$とする→$\cdots$->全てのマスを探索し終わったら終了

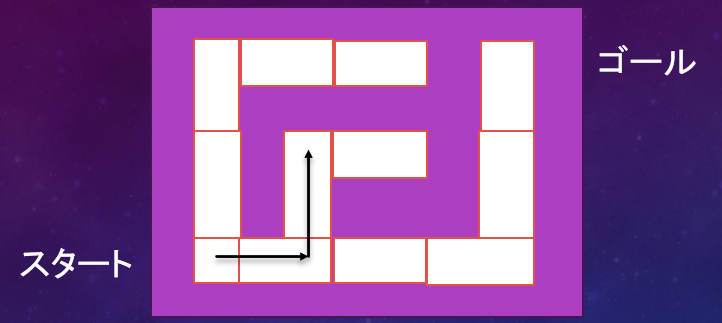
これはqueueなどを用いて実装できます。なぜ最短経路を計算したかを説明します。ゴールから、先ほど求めた最短経路の数字が1ずつ減るようにスタートまで辿ることで、一方通行のコースが生成できるからです。これは以下の画像を見たら直感的に分かると思います。

これをコースとして採用すれば、所望のランダムな一方通行なコースが生成できます。

なお、最短経路が極端に長過ぎたり短すぎたりする場合が考えられるので、最短経路の最小値と最大値を設定して、その範囲に収まらなければ再生成されるようにしています。

ちなみに、上の画像のマップは、ゲーム画面上では上のゲージと同期して、スタートから徐々にコースが生成されていくように描画しています。実際にはコース生成は一瞬で終了しますが、こういう演出にしたほうが面白いですよね(そうですよね？)。あとは、どこでワープを使うかの戦略も少し考えられます。

疑似3D

まずは描画する場所のイメージを持っておきましょう。左のマップ上にある青い丸はプレイヤーがいる場所で、青い三角形はプレイヤーが見えている視界の範囲です。

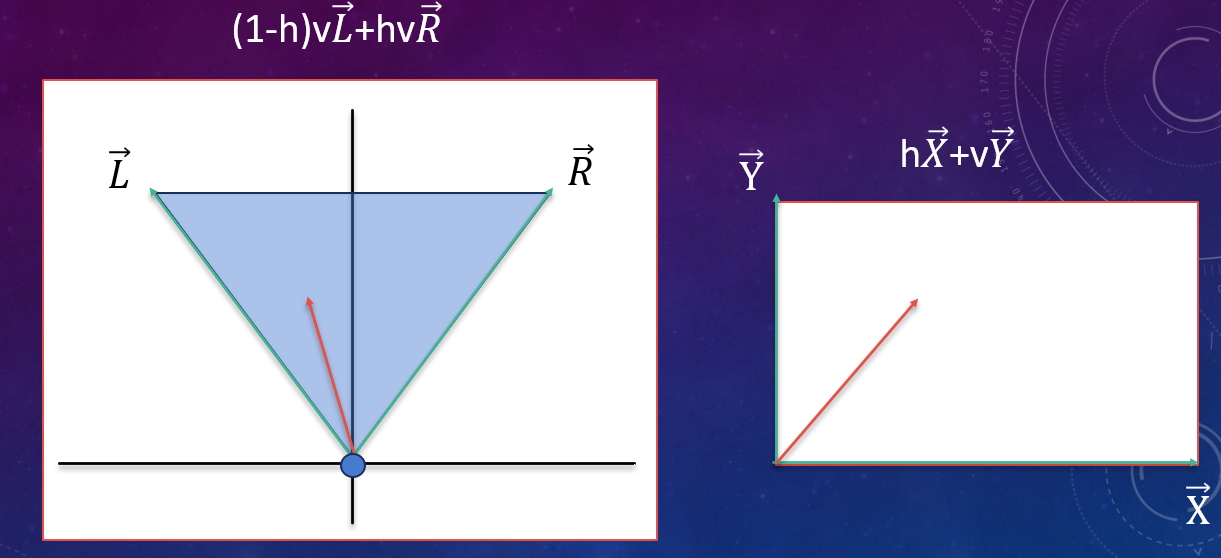
これを座標平面上に落とし込んでみましょう。左画像のように、ゲーム上のプレイヤーの視界の端をそれぞれ$\overrightarrow{L}, \overrightarrow{R}$とすると、青い三角形の範囲の任意の点は$0$から$1$を動く変数$h,v$を用いて以下のように表されます。

\begin{equation}
(1-h)v\overrightarrow{L}+hv\overrightarrow{R} \quad (0\le h\le 1,\,0\le v\le 1)
\end{equation}

また、右画像のように、実際のプレイヤーが見ている画面において$\overrightarrow{X},\overrightarrow{Y}$を設定します。ここで、先ほど用いた変数$h,v$を用いて任意の点は以下のように表されます。

\begin{equation}
h\overrightarrow{X}+v\overrightarrow{Y} \quad (0\le h\le 1,\,0\le v\le 1)
\end{equation}

さて、上で表した2式において、$h$と$v$は共通ですから、ゲーム上のプレイヤーの視界と実際のプレイヤーが見る画面の任意の点が一対一に対応していることがわかります。

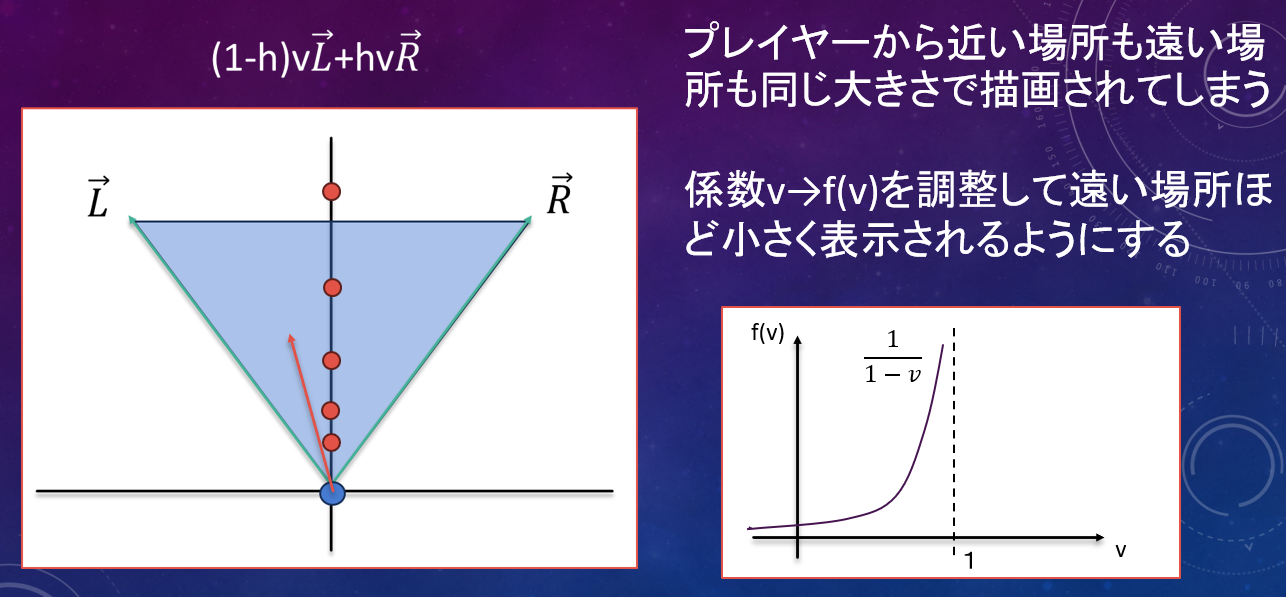
これでゲーム上のプレイヤーの視界を、実際のプレイヤーが見る画面上に映し出すことはできますが、このままだと疑似3Dとはなりません。いま、$v$を等間隔で増やしていくと、ゲーム上のプレイヤーからの距離も等間隔で遠ざかっていき、これだとプレイヤーから近い場所と遠い場所が同じ大きさで描画されてしまいます。つまり、遠近感が表現されていません。

ここで、$v$をうまいことある関数$f(v)$に変更して、遠い場所ほど小さく表示するようにできればこの問題は解決でき、疑似3Dを実装できそうです。

$v$を0から1まで等間隔で増やしていった時、$v$が小さい時は少しずつ$f(v)$が増え、$v$が大きくなってくると$f(v)$の増加具合が大きくなっていくような$f(v)$を採用すれば、近い場所が大きく、遠い場所が小さく表示されるという遠近感が表現できます。さらに、$f(v)$は当然1より大きくなりますから、描画範囲は下図の青い三角形の中に留まらず、マップを構成している二次元配列の中であれば更に遠い点まで描画することができます！

補足
$v=1$のとき$f(v)$の計算時にゼロ割りが発生してしまいますが、実際には$v$を$0\le v \le (1よりちょっと小さい数)$で動かして回避しています。

工夫点

色を塗り替える処理

通常は塗る色を変更する際に、色を指定する変数を変更すると思いますが、これがかなり重くなる要因になります。より単純なグラフィックアプリでもかなり重くなります。これを解決するために、あらかじめ利用する色全てに対して変数を用意しました。これだけで驚くほど動作が軽くなります。ダブルバッファリングと合わせればかなりヌルヌルでストレスなく遊べる程度になります。

キー入力の受付方法

課題ではあらかじめターミナルに入力されたキーを読み込む処理を記述したコードが配布されていたのですが、これにはいくつか問題がありました。

1. 同時押しに対応していない
   1文字ずつ読み込むので同時にキー入力に対する応答が行えません。

2. 長押しをするときに、1文字目と2文字目の入力の間に時間がかかる
   実際に同じキーの長押しをしてみれば分かると思います。これのせいでかなり操作性が悪くなります。

3. 単純に処理が遅い
   そのままです。

これはすべて#include <X11/keysym.h>により解決しました。

空の描画

地平線を画面最上部から少し低くして、画面上側は常に空が描画されるようにした。こっちのほうが見栄えが良くなりました。

セーブデータの保存

ファイルを使ってセーブデータを保存できるようにしました。上位タイムや統計、実績を保存できます。統計・実績を眺めるのが好きなので実装して良かったです。

ゲーム性

正直一番苦労しました。疑似3Dを使った良さそうなゲームで安直にレーシングを作り始めました。しかし、新規性を取り込もうと何か要素を足そうと思うと全然思いつかず苦労しました。切実に発想力がほしい。

あとがき

意外と基本的な数学だけで擬似3Dを表現することができて面白かったです。
普段は競技プログラミングをやっているので、BFSなどのアルゴリズムをゲーム制作に有効活用できたのはとても嬉しかったです。
Unityなどのゲームエンジンで簡単に実装できることも全て自分から作らないといけないので大変でしたが、オブジェクトの配置などをしないので、すべてプログラミングで実装が完結します。コーディングは好きなので楽しかったです。いい経験になりました。