MXNet Tutorialを順番にやっていくメモ(頑張って最後まで進む……)
Symbol
前節のNDArrayだけでも科学計算は可能なため、これで全ての計算が済むのではないか?という疑問が生まれるかもしれない.
MXNetではシンボリックに書けるSymbol APIを提供している. シンボリックな書き方ではステップバイステップに計算を記述するのではなく、最初に計算グラフを定義する.
グラフにはの入出力のPlaceholderが含まれており、これをコンパイルしたのち、NDArrayを出力するような関数を与えて実行する...Caffeのネットワークの設定とTheanoのシンボリックな書き方にSymbol APIは似ている.
シンボリック = 宣言的、とほぼ同義の模様
シンボリックなアプローチのもう一つの長所は最適化.
命令的に記述するとそれぞれの計算の際、その先何が必要になるのかわからない.
シンボリックな書き方では、アウトプットが事前に定義されているので、中間でのメモリを再割り当てして即座に計算ができる.
また同じネットワークでもメモリの必要量が小さくなる.
どちらの書き方がいいかはここで議論
ひとまずこの章ではSymbol APIについて述べる
グラフィカルな説明はここ参照
基本的なSymbol の構築
基本的な演算
a + bの表現方法. 最初にmx.sym.Variableでプレースホルダを作成する(作成時に名前を与える).
次に + で繋げてcを定義、この際自動で命名される.
import mxnet as mx
a = mx.sym.Variable('a') # aを抜くとエラー
b = mx.sym.Variable('b')
c = a + b
(a, b, c) # _plus0とcには自動で命名
(<Symbol a>, <Symbol b>, <Symbol _plus0>)
NDArrayの演算のほとんどがSymbleに対しても適用可能.
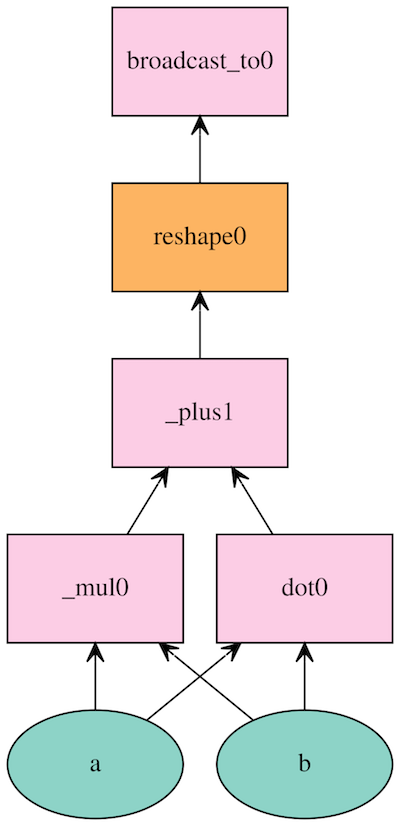
# 要素ごとのかけ算
d = a * b
# 行列積
e = mx.sym.dot(a, b)
# 変形
f = mx.sym.Reshape(d+e, shape=(1,4))
# ブロードキャスト
g = mx.sym.broadcast_to(f, shape=(2,4))
mx.viz.plot_network(symbol=g) # ネットワーク可視化
bindで入力を与えて評価する(詳細はこの後)
基本的なニューラルネット
ニューラルネットの層についても提供.
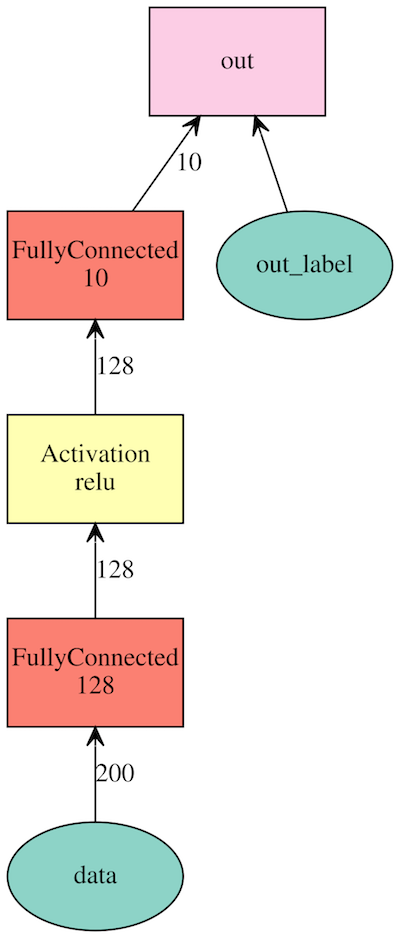
2層全結合ネットワークの記述例.
# 出力グラフは場合によるとのこと
net = mx.sym.Variable('data')
net = mx.sym.FullyConnected(data=net, name='fc1', num_hidden=128)
net = mx.sym.Activation(data=net, name='relu1', act_type="relu")
net = mx.sym.FullyConnected(data=net, name='fc2', num_hidden=10)
net = mx.sym.SoftmaxOutput(data=net, name='out')
mx.viz.plot_network(net, shape={'data':(100,200)})
それぞれのsymbolはユニークなな名前を持つ. NDArrayとSymbolは両方ともひとつのテンソルを示し演算子はテンソル間の計算を示している。演算子はSymbol(もしくはNDArray)を入力として受け取り、また場合によっては隠れ層の数(hidden_num)や活性化関数の種類(act_type)などハイパーパラメータを受け取って、出力する.
symbolをいくつかの引数を持つ関数として見ることもでき、この関数コールで引数一覧を見ることができる.
net.list_arguments()
['data', 'fc1_weight', 'fc1_bias', 'fc2_weight', 'fc2_bias', 'out_label']
mx.sym.Variable('data')
<Symbol data>
下記のパラメータやインプットがそれぞれのSymbolに必要
-
data: 変数dataに対して入力するデータ -
fc1_weight,fc1_bias: 最初の全結合層fc1の重みとバイアス -
fc2_weight,fc2_bias: 最初の全結合層fc2の重みとバイアス -
out_label: Lossに必要なラベル
明示的に宣言することもできる
net = mx.symbol.Variable('data')
w = mx.symbol.Variable('myweight')
net = mx.symbol.FullyConnected(data=net, weight=w, name='fc1', num_hidden=128)
net.list_arguments()
['data', 'myweight', 'fc1_bias']
上の例ではFullyConnectedへはdata, weight, biasの入力が三つ
と書かれているがコードにバイアスはなさそう、さらにいうと略記symを使っていない・・・
より複雑な構築
MXNetではディープラーニングでよくつかわる層について最適化されたSymbolを提供.
新しい演算子もPythonで定義可能
次の例では要素ごとにSymbolを足し算した後、全結合層へ渡している
lhs = mx.symbol.Variable('data1')
rhs = mx.symbol.Variable('data2')
net = mx.symbol.FullyConnected(data=lhs + rhs, name='fc1', num_hidden=128)
"""これは普通の演算ではなかろうか"""
net.list_arguments()
['data1', 'data2', 'fc1_weight', 'fc1_bias']
単一方向の構築だけでなくよりフレキシブルな構築も可能
data = mx.symbol.Variable('data')
net1 = mx.symbol.FullyConnected(data=data, name='fc1', num_hidden=10)
print(net1.list_arguments())
net2 = mx.symbol.Variable('data2')
net2 = mx.symbol.FullyConnected(data=net2, name='fc2', num_hidden=10)
composed = net2(data2=net1, name='composed') # netを関数として使用
print(composed.list_arguments())
['data', 'fc1_weight', 'fc1_bias']
['data', 'fc1_weight', 'fc1_bias', 'fc2_weight', 'fc2_bias']
この例ではnet2は既存のnet1をとる関数として指標されており、結果composedはnet1, net2両方の引数を持つことになる
symbol共通のPrefixをつけたいときはPrefixを利用できる
data = mx.sym.Variable("data")
net = data
n_layer = 2
for i in range(n_layer):
with mx.name.Prefix("layer%d_" % (i + 1)): # Prefix付与
net = mx.sym.FullyConnected(data=net, name="fc", num_hidden=100)
net.list_arguments()
['data',
'layer1_fc_weight',
'layer1_fc_bias',
'layer2_fc_weight',
'layer2_fc_bias']
モジュール化してのディープニューラルネットワークの構築
Google Inceptionのような深いネットワークを逐次記述するのは大変.
そのためモジュール化して再利用する
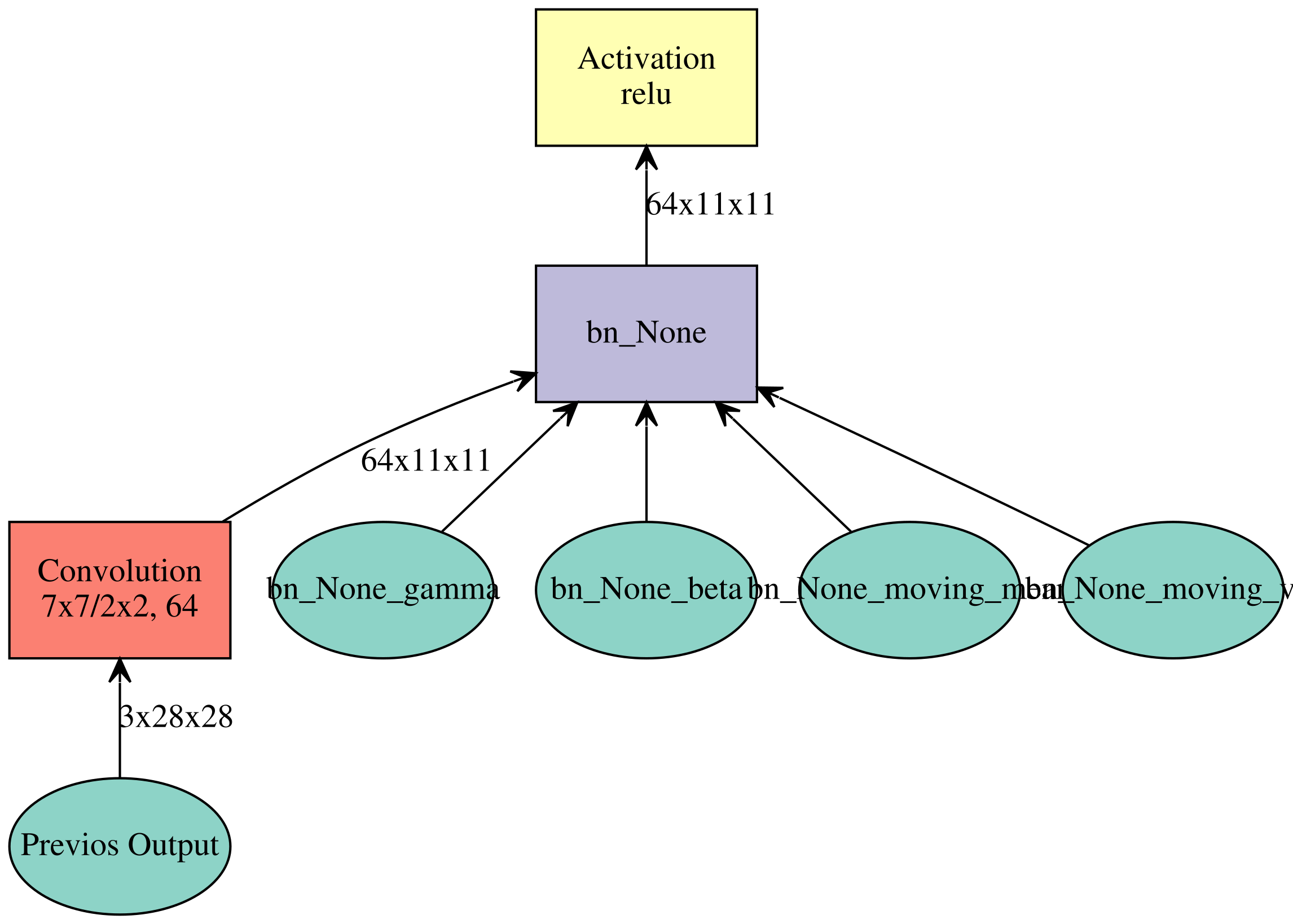
次の例では最初にfuctory function(畳み込み、Batch Normalize,ReLUのひとまりを生成)を定義
# Output may vary
def ConvFactory(data, num_filter, kernel, stride=(1,1), pad=(0, 0), name=None, suffix=''):
conv = mx.symbol.Convolution(data=data, num_filter=num_filter, kernel=kernel, stride=stride, pad=pad, name='conv_%s%s' %(name, suffix))
bn = mx.symbol.BatchNorm(data=conv, name='bn_%s%s' %(name, suffix))
act = mx.symbol.Activation(data=bn, act_type='relu', name='relu_%s%s' %(name, suffix))
return act
# 畳み込み→バッチノルム(バッチごとの正規化)→ReLUで活性化という一つのユニットを定義
prev = mx.symbol.Variable(name="Previos Output")
conv_comp = ConvFactory(data=prev, num_filter=64, kernel=(7,7), stride=(2, 2)) # 7×7のフィルタをストライド2でズラす、パディングはなし=> 11かけ11に
shape = {"Previos Output" : (128, 3, 28, 28)}
mx.viz.plot_network(symbol=conv_comp, shape=shape)
これを利用してInceptionを組む
# @@@ AUTOTEST_OUTPUT_IGNORED_CELL
def InceptionFactoryA(data, num_1x1, num_3x3red, num_3x3, num_d3x3red, num_d3x3, pool, proj, name):
# 1x1
c1x1 = ConvFactory(data=data, num_filter=num_1x1, kernel=(1, 1), name=('%s_1x1' % name))
# 3x3 reduce + 3x3
c3x3r = ConvFactory(data=data, num_filter=num_3x3red, kernel=(1, 1), name=('%s_3x3' % name), suffix='_reduce')
c3x3 = ConvFactory(data=c3x3r, num_filter=num_3x3, kernel=(3, 3), pad=(1, 1), name=('%s_3x3' % name))
# double 3x3 reduce + double 3x3
cd3x3r = ConvFactory(data=data, num_filter=num_d3x3red, kernel=(1, 1), name=('%s_double_3x3' % name), suffix='_reduce')
cd3x3 = ConvFactory(data=cd3x3r, num_filter=num_d3x3, kernel=(3, 3), pad=(1, 1), name=('%s_double_3x3_0' % name))
cd3x3 = ConvFactory(data=cd3x3, num_filter=num_d3x3, kernel=(3, 3), pad=(1, 1), name=('%s_double_3x3_1' % name))
# pool + proj
pooling = mx.symbol.Pooling(data=data, kernel=(3, 3), stride=(1, 1), pad=(1, 1), pool_type=pool, name=('%s_pool_%s_pool' % (pool, name)))
cproj = ConvFactory(data=pooling, num_filter=proj, kernel=(1, 1), name=('%s_proj' % name))
# concat
concat = mx.symbol.Concat(*[c1x1, c3x3, cd3x3, cproj], name='ch_concat_%s_chconcat' % name)
return concat
prev = mx.symbol.Variable(name="Previos Output")
in3a = InceptionFactoryA(prev, 64, 64, 64, 64, 96, "avg", 32, name="in3a")
mx.viz.plot_network(symbol=in3a, shape=shape)
完成しているものの例はここ
複数のSimbolのグルーピング
複数のLossのレイヤを持つようなニューラルネットを組むときは、mxnet.sym.Groupでグルーピングが可能
net = mx.sym.Variable('data')
fc1 = mx.sym.FullyConnected(data=net, name='fc1', num_hidden=128)
net = mx.sym.Activation(data=fc1, name='relu1', act_type="relu")
out1 = mx.sym.SoftmaxOutput(data=net, name='softmax')
out2 = mx.sym.LinearRegressionOutput(data=net, name='regression')
group = mx.sym.Group([out1, out2])
group.list_outputs()
['softmax_output', 'regression_output']
NDArrayとの関連
NDArrayは命令的なインターフェースを提供、計算は文ごとに評価される.
Symbolは宣言的なプログラミングに近い、最初に計算構造を宣言してそれからデータを評価.正規表現やSQLに近い.
NDArrayの利点
- 単純
- for, if-elseなどのプログラミング言語の特徴やNumPyなどのライブラリを活かしやすい
- ステップバイステップでのデバッグが行いやすい
Symbolの利点
- NDArrayの持つ関数のほぼ全てが提供されている(+, *, sin, reshapeなど)
- 保存と読み込み、ビジュアライズが簡単
- 計算やメモリ利用の最適化が行いやすい
Symbol の操作
SymbolとNDArrayの違いは上に述べた通り、ただしSymbolも直接操作することもできる.
ただし.moduleパッケージで大体はラップされていることに留意.
Shape Inference
それぞれのSymbolに対して、引数、付加的な情報、出力を求めることができる.出力の形やsymbolの型を、入力の形や引数の型から推定も可能、これでメモリ割り当てをやりやすくする.
# すっかり忘れがちだが c = a + b
arg_name = c.list_arguments() # 入力の名前
out_name = c.list_outputs() # 出力の名前
# 入力から出力の形を推定
arg_shape, out_shape, _ = c.infer_shape(a=(2,3), b=(2,3))
# 入力から出力の型を推定
arg_type, out_type, _ = c.infer_type(a='float32', b='float32')
print({'input' : dict(zip(arg_name, arg_shape)),
'output' : dict(zip(out_name, out_shape))})
print({'input' : dict(zip(arg_name, arg_type)),
'output' : dict(zip(out_name, out_type))})
{'output': {'_plus0_output': (2, 3)}, 'input': {'b': (2, 3), 'a': (2, 3)}}
{'output': {'_plus0_output': <class 'numpy.float32'>}, 'input': {'b': <class 'numpy.float32'>, 'a': <class 'numpy.float32'>}}
データによるバインドと評価
symbolcを評価するには引数としてデータをを与える必要がある.
これをするにはbindメソッドを利用する.これはコンテクストとfree valuable名とNDArrayのマッピングをした辞書を渡すとexecuterを返すメソッド.
exeutorからはforwardメソッドで評価が実行でき、output属性から結果が取り出せる.
ex = c.bind(ctx=mx.cpu(), args={'a' : mx.nd.ones([2,3]),
'b' : mx.nd.ones([2,3])})
ex.forward()
print('number of outputs = %d\nthe first output = \n%s' % (
len(ex.outputs), ex.outputs[0].asnumpy()))
number of outputs = 1
the first output =
[[ 2. 2. 2.]
[ 2. 2. 2.]]
同じSymbolを異なるコンテクスト(GPU)、異なるデータで評価もできる
ex_gpu = c.bind(ctx=mx.gpu(), args={'a' : mx.nd.ones([3,4], mx.gpu())*2,
'b' : mx.nd.ones([3,4], mx.gpu())*3})
ex_gpu.forward()
ex_gpu.outputs[0].asnumpy()
array([[ 5., 5., 5., 5.],
[ 5., 5., 5., 5.],
[ 5., 5., 5., 5.]], dtype=float32)
evalによる評価も可能、これはbindとforwardを束ねたもの
ex = c.eval(ctx = mx.cpu(), a = mx.nd.ones([2,3]), b = mx.nd.ones([2,3]))
print('number of outputs = %d\nthe first output = \n%s' % (
len(ex), ex[0].asnumpy()))
number of outputs = 1
the first output =
[[ 2. 2. 2.]
[ 2. 2. 2.]]
読み込みと保存
NDArrayと同様、pickleにできてsave, loadもできる.
ただSymbolはグラフであり、グラフは連続した計算から成り立っている。これらは出力のSymbolで暗黙的に表現されるので、出力Symbolのグラフをシリアライズする.
JSONでシリアライズすると可読性が上がるが、これにはtojsonを利用する.
print(c.tojson())
c.save('symbol-c.json')
c2 = mx.symbol.load('symbol-c.json')
c.tojson() == c2.tojson()
{
"nodes": [
{
"op": "null",
"name": "a",
"inputs": []
},
{
"op": "null",
"name": "b",
"inputs": []
},
{
"op": "elemwise_add",
"name": "_plus0",
"inputs": [[0, 0, 0], [1, 0, 0]]
}
],
"arg_nodes": [0, 1],
"node_row_ptr": [0, 1, 2, 3],
"heads": [[2, 0, 0]],
"attrs": {"mxnet_version": ["int", 1000]}
}
True
カスタムシンボル
mx.sym.Convolution、mx.sym.Reshapeのような演算はパフォーマンスのためC++でインプリされている.
MXNetではPythonのような言語を使って新しい演算モジュールを作ることもできる、詳しくはこちらを参照
Softmaxを継承して手前実装して見る感じ
発展的な利用方法
型キャスト
通常32bit小数点だが、高速化のために精度の低い型を利用することも可能.
mx.sym.Cast で型変換を行う
a = mx.sym.Variable('data')
b = mx.sym.Cast(data=a, dtype='float16')
arg, out, _ = b.infer_type(data='float32')
print({'input':arg, 'output':out})
c = mx.sym.Cast(data=a, dtype='uint8')
arg, out, _ = c.infer_type(data='int32')
print({'input':arg, 'output':out})
{'output': [<class 'numpy.float16'>], 'input': [<class 'numpy.float32'>]}
{'output': [<class 'numpy.uint8'>], 'input': [<class 'numpy.int32'>]}
変数の共有
Symbol間の共有は、同じアレイにSymbolをバインドすることで可能
a = mx.sym.Variable('a')
b = mx.sym.Variable('b')
c = mx.sym.Variable('c')
d = a + b * c
data = mx.nd.ones((2,3))*2
ex = d.bind(ctx=mx.cpu(), args={'a':data, 'b':data, 'c':data}) # dataを入力値として共有
ex.forward()
ex.outputs[0].asnumpy()
array([[ 6., 6., 6.],
[ 6., 6., 6.]], dtype=float32)
- Python 3 + Ubuntu, GPU環境で学習中
- 全文和訳しているわけではないです、あくまでメモ程度に
- Jupyterからの出力に手を入れただけなのでレイアウト崩れるやも…
途中モジュールの呼び出し方が定まっていない? (symと呼んだりsymbolと呼んだり)とまだまだチュートリアルとして定まっていない印象を受けました。
次はmoduleの予定。