Digital Identity技術勉強会 #iddanceAdvent Calendar 2024

RSAからECDSAへ、そしてその先へ

Last updated at 2024-12-16Posted at 2024-12-15

デジタル署名とは？

ある日のFacebookのTLで流れていた１つの図。あるアイデンティティ系書籍のデジタル署名の説明です。これを見て違和感を感じたとのTLでした。皆さんは違和感ありますか？

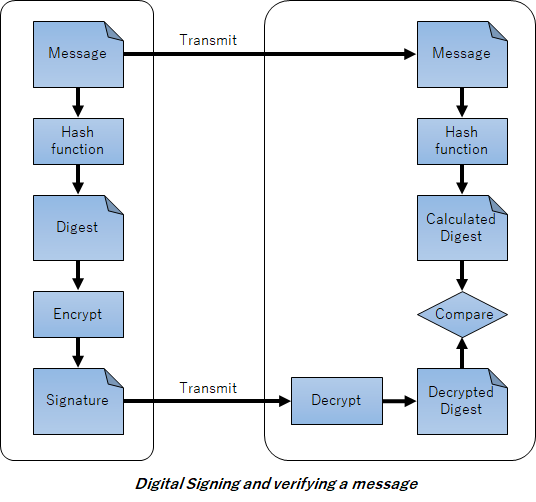
この図では左側が署名者の手順で右側が検証者の手順になっています。この中で署名値（Signature）を得るために以下の手順となっています。

署名手順（RSA）

対象データ（Message）を用意する。
ハッシュ関数（Hash function）でハッシュ値（Digest）を計算する。
ハッシュ値を署名鍵（秘密鍵）で暗号化（Encrypt）して署名値（Signature）を計算する。

検証する場合には以下の手順となっています。

検証手順（RSA）

対象データ（Message）を取得する。
ハッシュ関数（Hash function）でハッシュ値１（Calculated Digest）を計算する。
署名値（Signature）と検証鍵（公開鍵）を取得する。
署名値を検証鍵（公開鍵）で復号（Decrypt）してハッシュ値２（Decrypted Digest）を得る。
ハッシュ値１とハッシュ値２を比較して一致したら検証成功とする。

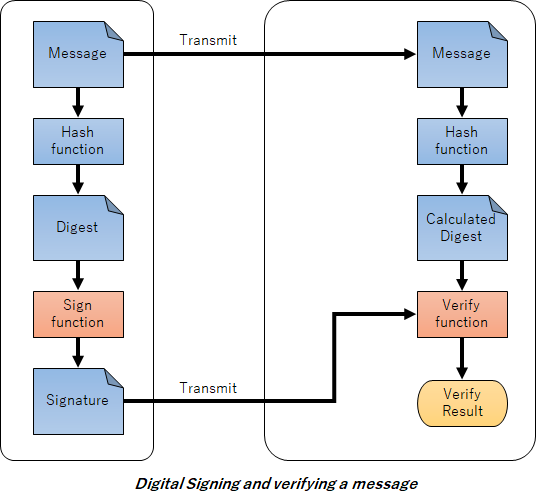
間違ってはいません。RSA暗号方式ならと言う前提条件付きですが。なので（RSA）と付けています。なお署名が 署名鍵（秘密鍵）で暗号化（Encrypt） して、検証が 検証鍵（公開鍵）で復号（Decrypt） しているのですが、署名は公開するもので秘密にするものではないので「署名鍵（秘密鍵）で復号」と言うべきだ。と言う方もいるそうですがメンドクサイのでここでは無視します。それではDSA暗号方式やECDSA暗号方式の場合にはどうなるでしょうか。それが以下の図となります。

最初の図に署名鍵（秘密鍵）と検証鍵（公開鍵）が無かったので上の図でも省いていますが、この場合の署名手順は以下となります。

署名手順（DSA/ECDSA）

対象データ（Message）を用意する。
ハッシュ関数（Hash function）でハッシュ値（Digest）を計算する。
ハッシュ値と署名鍵（秘密鍵）を入力として署名関数（Sign function）を使って署名値（Signature）を計算する。

最後以外は同じですね。では検証はどうなるでしょう？

検証手順（DSA/ECDSA）

対象データ（Message）を取得する。
ハッシュ関数（Hash function）でハッシュ値（Calculated Digest）を計算する。
署名値（Signature）と検証鍵（公開鍵）を取得する。
ハッシュ値と署名値と検証鍵（公開鍵）を入力として検証関数（Verify function）を使って検証結果（真または偽）を得る。

何が違うのでしょう？暗号化（Encrypt）の代わりに署名関数（Sign function）が、復号化（Decrypt）の代わりに検証関数（Verify function）になっていますね。どうしてこうなるのでしょう？と言うお話をします。暗号を専門にしている人からはツッコミもあるかもしれませんが、OpenSSLを例にプログラマ的に見て行きます。

RSA暗号方式のデジタル署名

RSA暗号を使ったデジタル署名の仕様はPKCS#1で定義されており、現在だとRFC 8017「PKCS#1: RSA Cryptography Specifications Version 2.2」を参照します。この中の「A.2.4. RSASSA-PKCS-v1_5」に署名値のDigestInfoのASN.1定義があります。これをDERエンコードして利用します。

DigestInfo ::= SEQUENCE {
    digestAlgorithm DigestAlgorithm,
    digest OCTET STRING
}

見て分かる通り、ハッシュ方式（digestAlgorithm）とハッシュ値（digest）で構成されています。つまりハッシュ値そのものと言うことですね。これをRSA暗号により暗号化するのですが、RSA暗号の場合にはサイズが鍵長の倍数である必要があるので、不足分をパディング（padding）してから暗号化します。よって手順としては以下と言うことになります。

RSA暗号による署名値の生成手順：

署名対象のハッシュ値を計算する。
ハッシュ値をDigestInfoの形にしてDERエンコードする。
DERエンコードされたデータにパディングして鍵長倍数サイズにする。
RSA暗号を使い署名鍵（秘密鍵）により暗号化したものが署名値となる。

検証する際には逆の手順（検証鍵で復号する）で署名対象のハッシュ値を得て、自分で署名対象から計算したハッシュ値と突合して一致確認をすることでVALID/INVALIDの判定をします。OpenSSL等ではこのような手順はAPIの中で行われており、RSA暗号により署名する場合には署名値の中はブラックボックスとして扱い単なるバイナリデータとして利用します。検証も署名対象のハッシュ値と署名値と検証鍵（公開鍵）を入力として結果がBoolean値のTRUE/FALSEで返されます。

なおダイジェストアルゴリズム（DigestAlgorithm）としては以下が例として載っています。ハッシュアルゴリズムのOID以外にパラメーター（PARAMETERS）の指定も可能になっています。

PKCS1-v1-5DigestAlgorithms    ALGORITHM-IDENTIFIER ::= {
    { OID id-md2        PARAMETERS NULL }|
    { OID id-md5        PARAMETERS NULL }|
    { OID id-sha1       PARAMETERS NULL }|
    { OID id-sha224     PARAMETERS NULL }|
    { OID id-sha256     PARAMETERS NULL }|
    { OID id-sha384     PARAMETERS NULL }|
    { OID id-sha512     PARAMETERS NULL }|
    { OID id-sha512-224 PARAMETERS NULL }|
    { OID id-sha512-256 PARAMETERS NULL }
}

パラメーターに関しては、署名生成時には「PARAMETERSにNULLを含む(SHALL)」となっており、検証時には「PARAMETERSにNULLが無くても検証できる(SHALL)」となっています。まあ最近では気にすることは無いと思いますがこれは参考まで。

ECDSA暗号方式のデジタル署名

DSA/ECDSAによる署名計算の仕様はRFC 6979「Deterministic Usage of the Digital Signature Algorithm (DSA) and Elliptic Curve Digital Signature Algorithm (ECDSA)」を参照します。この中の「2.4. Signature Generation」で署名手順が書かれており、ハッシュ値と署名鍵（秘密鍵）を入力として楕円曲線を利用した計算をおこない、最終的にはINTEGER値のペア(r,s)が署名値として出力されてきます。署名値のエンコード方法は標準ではカバーされていないとありますが、ASN.1形式で「rとsの順序で2つのINTEGERのシーケンスをDERエンコード」の利用が一般的な方法として記載されています。RFC 5480「Elliptic Curve Cryptography Subject Public Key Information」にANS.1の署名値の定義があり以下のようになっています。

ECDSA-Sig-Value ::= SEQUENCE {
    r  INTEGER,
    s  INTEGER
}

当たり前ですが署名値にはハッシュ値は含まれていませんしハッシュ値を取り出すことも出来ません。検証する場合には自分で計算した署名対象のハッシュ値と取得した署名値と検証鍵（公開鍵）を入力として結果がBoolean値のTRUE/FALSEで返されます。なおハッシュ方式に関しては署名アルゴリズムのOIDで判断することになります。RFC 5758「Internet X.509 Public Key Infrastructure: Additional Algorithms and Identifiers for DSA and ECDSA」を参照します。

ecdsa-with-SHA224 OBJECT IDENTIFIER ::= { iso(1) member-body(2)
    us(840) ansi-X9-62(10045) signatures(4) ecdsa-with-SHA2(3) 1 }

ecdsa-with-SHA256 OBJECT IDENTIFIER ::= { iso(1) member-body(2)
    us(840) ansi-X9-62(10045) signatures(4) ecdsa-with-SHA2(3) 2 }

ecdsa-with-SHA384 OBJECT IDENTIFIER ::= { iso(1) member-body(2)
    us(840) ansi-X9-62(10045) signatures(4) ecdsa-with-SHA2(3) 3 }

ecdsa-with-SHA512 OBJECT IDENTIFIER ::= { iso(1) member-body(2)
    us(840) ansi-X9-62(10045) signatures(4) ecdsa-with-SHA2(3) 4 }

なお楕円曲線には幾つか種類がありますが、ECDSAのデジタル署名では通常FIPS 146-4: Digital Signature Standard (DSS)で定義されている曲線である、NIST P-256/P-384/P-521が使われます。最後のP-521はP-512の間違いではありません。P-521が正しいカーブ名です。カーブに関してはパラメーター等で指定ができる場合があります。

OpenSSLによる公開鍵暗号の署名と検証

OpenSSLのVer3からは非推奨APIとなりましたが、OpenSSLでRSA暗号を利用して暗号化と復号をするAPIとして以下が提供されています。どのAPIも入力として、対象データとRSA鍵とパディング方式（通常はRSA_PKCS1_PADDING）を指定して結果データを返します。興味深いのは、秘密鍵による暗号化と公開鍵による復号、公開鍵による暗号化と秘密鍵による復号、の両方向をサポートしていることです。「え？公開鍵暗号方式なんだから当たり前でしょう？」とおっしゃると思いますが、実はこの特性は数ある公開鍵暗号方式のうちRSA暗号に特有だったりします。つまり実は珍しい特性なのです。普通は片方向のみをサポートしているのです。逆に言えばこの両方向の特性があるので、秘密鍵で暗号化を署名として、公開鍵で復号を検証として、利用できているのです。余談ですがWindowsのCAPI（Crypto API）では公開鍵で復号するようなAPIは提供されていません。ある意味正しいですね。

int RSA_public_encrypt(int flen, const unsigned char *from, unsigned char *to,
                       RSA *rsa, int padding);

int RSA_private_encrypt(int flen, const unsigned char *from, unsigned char *to,
                        RSA *rsa, int padding);

int RSA_public_decrypt(int flen, const unsigned char *from, unsigned char *to,
                       RSA *rsa, int padding);

int RSA_private_decrypt(int flen, const unsigned char *from, unsigned char *to,
                        RSA *rsa, int padding);

同様に署名と検証するAPIとして以下が提供されています。こちらもOpenSSL Ver3では非推奨となっています。署名では対象データ（ハッシュ値）とRSA鍵を入力として署名値を得ます。検証では対象データ（ハッシュ値）と署名値とRSA鍵を入力として検証結果としてVALID(1)かINVALID(1以外)を得ます。こちらは署名時には秘密鍵を検証時には公開鍵を指定します。なお「The following 2 functions sign and verify a X509_SIG ASN1 object inside PKCS#1 padded RSA encryption」との説明がありますので、内部ではPKCS#1パディングとRSA暗号化が行われることになります。

int RSA_sign(int type, const unsigned char *m, unsigned int m_length,
             unsigned char *sigret, unsigned int *siglen, RSA *rsa);

int RSA_verify(int type, const unsigned char *m, unsigned int m_length,
             const unsigned char *sigbuf, unsigned int siglen, RSA *rsa);

一方でECDSAは署名と検証のAPIのみが提供されています。暗号化/復号をする暗号方式ではないので当然ですね。こちらもOpenSSL Ver3では非推奨となっています。署名では対象データ（ハッシュ値）とRSA鍵を入力として署名値を得ます。検証では対象データ（ハッシュ値）と署名値とRSA鍵を入力として検証結果としてVALID(1)かINVALID(1以外)を得ます。ECDSAでも署名時には秘密鍵を検証時には公開鍵を指定します。

int ECDSA_sign(int type, const unsigned char *dgst, int dgstlen,
　             unsigned char *sig, unsigned int *siglen, EC_KEY *eckey);

int ECDSA_verify(int type, const unsigned char *dgst, int dgstlen,
                 const unsigned char *sig, int siglen, EC_KEY *eckey);

OpenSSLのEVPのAPI群

さてここまで分かりやすくするために、OpenSSL Ver3では非推奨のAPIばかり説明しましたが、ではVer3の署名と検証はどうなるでしょう？答えは公開鍵暗号方式に依存しないEVPのAPIの利用です。

int EVP_PKEY_sign(EVP_PKEY_CTX *ctx,
                  unsigned char *sig, size_t *siglen,
                  const unsigned char *tbs, size_t tbslen);

int EVP_PKEY_verify(EVP_PKEY_CTX *ctx,
                    const unsigned char *sig, size_t siglen,
                    const unsigned char *tbs, size_t tbslen);

なおEVPのAPIには暗号化と復号をおこなう以下も提供されていますが、基本的には暗号化には公開鍵を復号には秘密鍵を使います。

int EVP_PKEY_encrypt(EVP_PKEY_CTX *ctx,
                     unsigned char *out, size_t *outlen,
                     const unsigned char *in, size_t inlen);

int EVP_PKEY_decrypt(EVP_PKEY_CTX *ctx,
                     unsigned char *out, size_t *outlen,
                     const unsigned char *in, size_t inlen);

それではEVPのAPIによりRSA暗号の署名値の復号を公開鍵でおこなうにはどうするかと言えば、以下のAPIが提供されています。

int EVP_PKEY_verify_recover(EVP_PKEY_CTX *ctx,
                            unsigned char *rout, size_t *routlen,
                            const unsigned char *sig, size_t siglen);

EVP_PKEY_verify_recoverでRSA暗号を利用すると rout に公開鍵で復号された署名値が返されます。なおこのEVP_PKEY_verify_recoverは当然ですがRSA暗号では使えますが、DSA/ECDSA暗号では使えません。以下にEVPのAPIを使った署名手順を示します。なおエラーチェック等はしていないのでご注意を。

// 署名鍵初期化
EVP_PKEY_CTX *ctx = EVP_PKEY_CTX_new(pKey, NULL);
// 署名初期化
EVP_PKEY_sign_init(ctx);
if (EVP_PKEY_RSA == EVP_PKEY_type(EVP_PKEY_id(pKey))) {
    // RSAのみパディング方式を指定
    EVP_PKEY_CTX_set_rsa_padding(ctx, RSA_PKCS1_PADDING);
}
// ハッシュ方式を指定
EVP_PKEY_CTX_set_signature_md(ctx, EVP_sha256());
// 署名値サイズの取得
size_t siglen = EVP_PKEY_size(pKey);
sigval.resize(siglen);
// EVP署名実行
EVP_PKEY_sign(ctx, &sigval[0], &siglen, &digest[0], digest.size());
// 署名鍵解放
EVP_PKEY_CTX_free(ctx);

以下が検証手順です。

// 検証鍵初期化
EVP_PKEY_CTX *ctx = EVP_PKEY_CTX_new(pKey, NULL);
// 検証初期化
EVP_PKEY_verify_init(ctx);
if (EVP_PKEY_RSA == EVP_PKEY_type(EVP_PKEY_id(pKey))) {
    // RSAのみパディング方式を指定
    EVP_PKEY_CTX_set_rsa_padding(ctx, RSA_PKCS1_PADDING);
}
// ハッシュ方式を指定
EVP_PKEY_CTX_set_signature_md(ctx, EVP_sha256());
// EVP検証実行（rsltが1なら検証成功）
int rslt = EVP_PKEY_verify(ctx, &sigval[0], sigval.size(), &digest[0], digest.size());
// 検証鍵解放
EVP_PKEY_CTX_free(ctx);

上の実装ではRSA暗号でもECDSA暗号でも使えます。違いはRSA暗号ではパディング方式を指定する必要があることです。RSA暗号の鍵かどうかは「EVP_PKEY_RSA == EVP_PKEY_type(EVP_PKEY_id(pKey))」で判定できます。

今後OpenSSLでは新しい署名の為の暗号方式が出てきても基本的にはEVPのAPI群で対応することになるようです。確認はしていませんがおそらくPQC（耐量子暗号）でも同じだと思います。

なお余談になりますが、RSA暗号で検証に失敗する場合によくやるデバッグ方法として、署名値を復号してDigestInfoが取り出せれば検証鍵（公開鍵）は正しく、ハッシュ値が異なっていることが分かります。DigestInfoが取り出せなければ検証鍵（公開鍵）が誤っていることになります。一方ECDSA暗号で検証に失敗する場合には手の打ちようがありません。ハッシュ値と検証鍵（公開鍵）のどちらが間違っているか分からないのでちょっと苦労すると言うことがあります。PKIプログラマで一番デバッグで苦労するのがこの検証に失敗するケースだったりします。

ECDSA暗号の署名に関する問題点

上の方で書きましたがECDSAを使った署名の署名値は2つのINTEGERをSEQUENCEで繋いでDERエンコードした方式が一般的ですが標準化されていません。しかしOpenSSLの検証ではこのDERエンコードされた署名値しか利用できません。私が知っているECDSAの署名値フォーマットは以下の3パターンです。

パターン１：ANS.1/DERエンコード: これが正式と言って良いフォーマットです。OpenSSLではこのフォーマットで署名値を出力しますし、検証ではこのフォーマットのみ利用可能です。
パターン２：ASN.1/BERエンコード: DERは正規化されていますが、BERは単純にエンコードするだけで異なります。良く見かけるミスです。OpenSSLもVer1の頃はDER指定のデータにBERエンコードのデータを入れてもエラーになりませんでしたが、Ver3では厳しくなってエラーになります。実はAdobe Acrobatで署名するとこのフォーマットになっているような…
パターン３：2つのBIGINT値の単純結合: バイナリを2つに割って前をr値に後ろをs値に使います。単純にもほどがある。とは言えますがWindowsのCNGで署名するとこのフォーマットになります。

私も署名ライブラリを開発しているのですが、署名生成時にはパターン1のANS.1/DERエンコードで出力するようにして、検証時にはパターン2とパターン3をパターン1に変換して利用しています。面倒ですね。何故署名値のフォーマットを標準化しなかったのでしょうか…まあパターン2のDERエンコードが必要なところをBERエンコードしちゃうと言うのはPKIプログラミングではありがちなミスではあるんですが。Adobe Acrobatでもそのうちそっと直っていそうな気はします。

話を戻しましょう

と言うことで最初の図に戻ってみましょう。以下の図はRSA暗号とデジタル署名が同一の時代には正しいのですが、現在のようにECDSAへの暗号移行や更にはPQCへの暗号移行の時代には少しレガシーなのかなと言うことになります。いや正直を言えば私も昔は同じ図を使ってデジタル署名を説明していました。この資料の14ページとかですね。2015年の資料だからほぼ10年前です。その頃はまだデジタル署名暗号方式はRSA暗号方式とイコールだったのです。

しかしながら現在ではデジタル署名にECDSA暗号方式をはじめとした色々な暗号方式が前提となる時代です。今後の暗号移行（128ビットセキュリティへおよびPQCへの移行）も考えるとOpenSSLのEVP関数群のように暗号方式に依存しない説明が望ましいのではないでしょうか。

その先へ

次世代の公開鍵暗号の1つとして楕円曲線暗号（EC）がある訳ですが、実際にはデジタル署名のECDSA（楕円曲線を使ったDSA署名方式）と鍵交換のECDH（楕円曲線を使ったDH鍵交換方式）が実装となります。PQC（耐量子暗号）の公開鍵暗号のコンテストに関しても実装として「デジタル署名」と「鍵交換・暗号化」の実装に分かれており全く異なる暗号方式が使われています。「デジタル署名」と「鍵交換・暗号化」のどちらでも利用できるRSA暗号が変わっていたと言うことになります。ちなみにNIST（米国立標準技術研究所）のPQCコンテストの結果、以下の3方式が正式に採用となりました。

FIPS 203, Module-Lattice-Based Key-Encapsulation Mechanism Standard: 格子暗号を使う鍵交換アルゴリズム
FIPS 204, Module-Lattice-Based Digital Signature Standard: 格子暗号を使うデジタル署名アルゴリズム
FIPS 205, Stateless Hash-Based Digital Signature Standard: ハッシュ関数を使うデジタル署名アルゴリズム

なおNISTのPQCコンテストはまだ継続するようですので更に別の暗号方式が採用される可能性もあります。デジタル署名の暗号方式としてECDSAの次にデファクト標準となるのはどの暗号方式になるのでしょうか。PQC暗号方式は鍵サイズや署名値サイズが大きいと言う問題があるものが多くまだ決定打になる方式は決まっていないと言う理解です。業界で認められるのはどの暗号方式なのか見守って行きましょう。PKIプログラマとしては時間があればPQCも試したいところです。時間があればまた記事が書けると…良いなあw

おわりに…と余談（言い訳）

暗号を利用するプログラマとしては、そろそろRSA暗号前提の世界から多様な暗号方式を前提とした世界に移行した方が良いと考えています。以上この記事が皆さまのご参考になれば幸いです。

えーとこの記事は毎年参加している「Digital Identity技術勉強会 #iddance Advent Calendar 2024」の記事の1つです。「え？この記事のどこがアイデンティティの話やねん！署名じゃねえか！」と言われるでしょうね…いやまあそうなんですが…ネタが無かったと言うか…デジタル署名も認証に使うやん…と言うか………生暖かく笑って許して！（笑）

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up