はじめに
初めまして、leisurelyと申します。この記事は、経済学を勉強していく上で逃れることのできない「コブダグラス型生産関数」を3Dグラフを用いて可視化します。
なぜ、この記事を書こうと思ったのか。それは、教科書や講義で先生が黒板に書くコブダグラス型生産関数のグラフがわかりにくいからです。(教科書や先生を批判してるのではなく、紙や黒板という2次元に3次元グラフを描く、かつ初学者に理解してもらうには限界があるということです。)
当然、教科書や黒板のグラフで理解できる方もおられると思います。
それに加え、荒戸寛樹氏(https://twitter.com/hirokiarato )の一連のツイートでの「Rによるコブダグラス型生産関数の可視化」に感銘を受けたからです。
一連のツイート:
https://twitter.com/hirokiarato/status/1001466936989962240
https://twitter.com/hirokiarato/status/1001482183515586561
https://twitter.com/hirokiarato/status/1001491836785983488
私はRよりもPythonを使うことが多いので、Pythonでの実装を試みました。
実装はJupyter Notebook 上でPythonを用いて行います。
※この記事はプログラミングを学ぶのではなく、プログラミングというツールを用いて経済学をより理解するのが目的です。また、プログラミングわからないけれど結果だけ見たいという方のために、最後に結果を載せています。
コブダグラス型生産関数
念のため、コブダグラス型生産関数についておさらいをしておきます。生産量をY、資本をK、労働投入量をLとした場合に、
Y=K^{\alpha} L^{\beta}
で示される生産関数のことです。$\alpha$と$\beta$は正の定数を示しています。
$\alpha + \beta = 1$ ならば一次同次関数なります。今回は一次同次関数を扱っていきます。
コードの実装
さっそくコードの実装を行います。結果だけを見たい人は読み飛ばしていただいて構いません。
コードの実装にあたり「jupyter notebookで触れるプロットを描く(http://ksknw.hatenablog.com/entry/2016/08/04/233103 )」を参考にさせていただきました。と、言いたいところですが、9割コピペしています。
またコードの説明につきましても必要最小限にとどめています。詳しい説明は上記のURLにてお願いします。
ではコードです。
%matplotlib notebook
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
import numpy as np
def f(k, l):
return k**(1/2) * l**(1/2)
k = np.arange(0, 100, 2.5)
l = np.arange(0, 100, 2.5)
K, L = np.meshgrid(k, l)
Y = f(K, L)
fig = plt.figure()
ax = Axes3D(fig)
ax.set_xlabel("K")
ax.set_ylabel("L")
ax.set_zlabel("Y")
ax.plot_wireframe(K, L, Y)
plt.show()
以上が実装したコードになります。一つだけ説明を行いますと、
def f(k, l):
return k**(1/2) * l**(1/2)
この関数の定義において$k$, $l$ の指数を変更させることでグラフの形状と任意の$n$次同次関数に変化させることができます。
結果:可視化されたコブダグラス型生産関数
上記のコードを実行すると以下のようなグラフがプロットされます。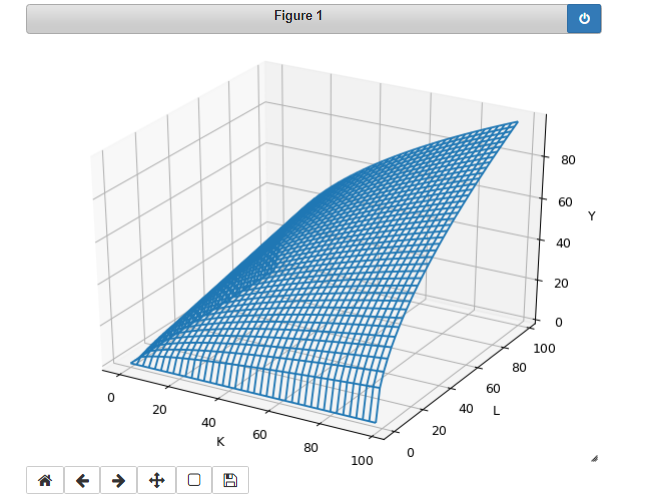
先生が苦労しつつ黒板に書かれていたグラフだ‼
このグラフは様々な角度から見ることもできます。
以上がコブダグラス型生産関数の可視化になります。
皆様の経済学の勉強の参考になれば幸いです。
2019.08.22追記
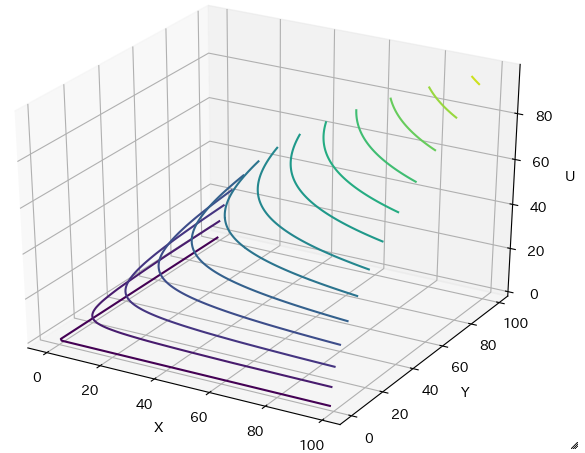
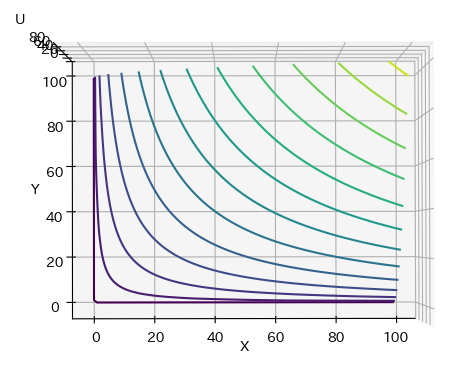
メッシュでのプロットでは等量曲線がわかりにくいので等高線によるプロットも行いました。
どちらかというと効用最大化問題の無差別曲線を理解するために書きます。まぁ基本は一緒です。
縦軸・横軸がY・X、高さがUに代わっていますが気にしないでください。(この場合、等量曲線じゃなくて無差別曲線ですね)
ax.plot_wireframe(K, L, Y) #これを
ax.contour(K, L, Y, 15) #これに書き直す。最後の数字は等高線の数
コードは上記のコードの一部を書き直してください。