【kaggle】特徴量エンジニアリング - 相互情報量【備忘翻訳】

はじめに

当記事はkaggleのLearnのFeature EngineeringのMutual Informationを翻訳して備忘としたものです。
拙い英語力なので間違い等あればご指摘いただけたらと思います。

まとめ:【kaggle】翻訳記事まとめ【備忘翻訳】
前:【kaggle】特徴量エンジニアリング - 特徴量エンジニアリングとは【備忘翻訳】
次:【kaggle】特徴量エンジニアリング - 特徴量の作成【備忘翻訳】

当記事に含まれるコードはkaggle内のnotebook内で正常に動作します。動作を試したい場合はkaggleのnotebookで試してください。

---

相互情報量

最も可能性の高い特徴量を特定します。

イントロダクション

新しいデータセットに初めて遭遇すると圧倒されるように感じることがあります。何百、何千もの特徴量が説明もなしに提示されることがあります。どこから始めればいいのでしょうか？

よりよい最初のステップは、特徴量とターゲットの関連性を測定する機能であるfeature utility metricを使用してランキングを構築することです。そうすれば、最初に開発する最も有用な特徴量の小さなセットを選択でき、時間を有効に活用できるという自信が高まります。

ここで使用する指標は「相互情報量」と呼ばれます。相互情報量は、２つの量の関係を測定するという点で相関によく似ています。相互情報量の利点は、相関関係が線形の関係のみを検出するのに対し、あらゆる種類の関係を検出できることです。

相互情報量は汎用性に優れた指標であり、どのモデルを使用するかまだ分からない特徴量開発のスタート時に役立ちます。それは:

• 使いやすく解釈しやすく
• 計算効率が高く
• 理論的に根拠があり
• 過剰学習に耐性があり
• あらゆる関連を検出できる

相互情報量とその測定対象

相互情報量は、不確実性の観点から関係性を示します。２つの量間の相互情報量(mutual information (MI)) は、一方の量の影響が他方の量の不確実性をどの程度低減するかを測る尺度です。
特徴量の価値が分かれば、ターゲットに対する確度はどれほど高まるでしょうか？

これはエイムズ住宅データからの例です。この図は住宅の外観品質と販売価格の関係を示しています。各点は住宅を表しています。

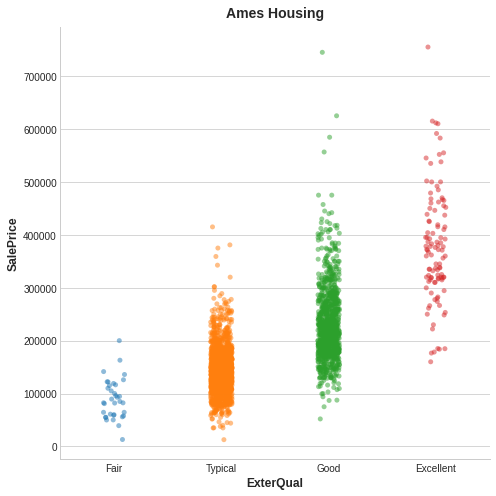
家の外観品質を知ることで、その販売価格に関する不確実性が軽減されます。

図から、ExterQualの値から、対応するSalePriceについての相関関係がより核心を持てるようになることが分ります。ExterQualの各カテゴリは、SalePliceを特定の範囲内に集中させる傾向があります。ExterQualがSalePriceと持つ相互情報量は、ExterQualの4つの値に対するSalePriceの不確実性の平均的に減少させています。例えば、FairはTypicalよりも発生頻度が低いため、MIスコアではFairの重み付けが低くなります。

(技術的メモ:私たちが不確実性と呼んでいるものは、「エントロピー」と呼ばれる情報理論の量を使用して測定されます。変数のエントロピーはおおよそ:『その変数の発生を説明するために、平均して何回の「はい」か「いいえ」の質問がひつようになるか』を意味します。質問の数が増えるほど、変数に関する不確実性も増します。相互情報量とは、機能がターゲットに関して答えると予想される質問の数です。)

相互情報量スコアの解釈

情報量間の最小相互情報量は0.0です。MIがゼロの場合は、情報量は独立しており、どちらも他方について何も伝えることができません。逆に言えば、理論的にはMIに上限はありません。ただし、実際には2.0を超える値は稀です。(相互情報量は対数量であるため、非常にゆっくりと増加します。)

次の図は、MI値が、特徴量とターゲットとの関連性の種類と程度にどのように対応するかを示しています。

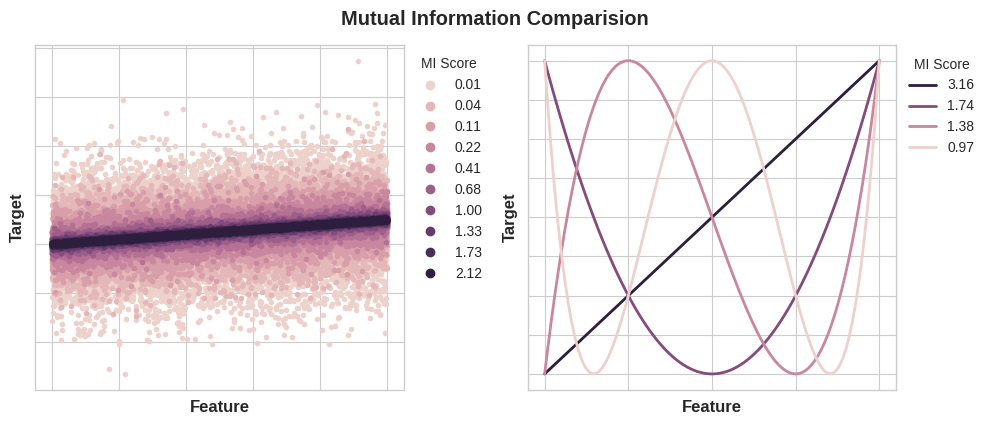
左図:特徴量とターゲット間の依存関係が強くなるにつれて、相互情報量が増加します。右図:相互情報量は、あらゆる種類の関連性(相関関係のような線形関係だけではない)を捉えることができます。

相互情報量を適用するときに覚えておくべき点は次の通りです。

• MIは、特徴量自体を考慮した場合の、ターゲットの予測因子としての相対的な可能性を理解するのに役立ちます。
• ある特徴量は他の特徴量と相互作用すると非常に有益になるが、単独ではそれほど有益ではない可能性があります。MIは特徴量間の相互作用を検出できません。これは単変量指数です。
• 特徴量の実際の有用性は、それを使用するモデルによって異なります。特徴量は、その特徴量とターゲットとの関係がモデルで学習できる範囲でのみ役立ちます。特徴量のMIスコアが高いからと言って、モデルがその情報を使って何かを実行できるわけではありません。関連性を明らかにするには、まず特徴量を変換する必要がある場合があります。

例 - 1985 自動車

自動車データセットは、1985年モデルの自動車193台で構成されています。このデータセットの目標は、make、body_style、horsepowerなど、自動車の23の特徴量から自動車の価格(ターゲット)を予測することです。この例では、相互情報量を使用して特徴量をランク付けし、データの視覚化によって結果を調査します。

下の折り畳みは、ライブラリのインポートとデータセットを行っています。

setup

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns

plt.style.use("seaborn-whitegrid")

df = pd.read_csv("../input/fe-course-data/autos.csv")
df.head()

	symboling	make	fuel_type	aspiration	num_of_doors	body_style	drive_wheels	engine_location	wheel_base	length	...	engine_size	fuel_system	bore	stroke	compression_ratio	horsepower	peak_rpm	city_mpg	highway_mpg	price
0	3	alfa-romero	gas	std	2	convertible	rwd	front	88.6	168.8	...	130	mpfi	3.47	2.68	9	111	5000	21	27	13495
1	3	alfa-romero	gas	std	2	convertible	rwd	front	88.6	168.8	...	130	mpfi	3.47	2.68	9	111	5000	21	27	16500
2	1	alfa-romero	gas	std	2	hatchback	rwd	front	94.5	171.2	...	152	mpfi	2.68	3.47	9	154	5000	19	26	16500
3	2	audi	gas	std	4	sedan	fwd	front	99.8	176.6	...	109	mpfi	3.19	3.40	10	102	5500	24	30	13950
4	2	audi	gas	std	4	sedan	4wd	front	99.4	176.6	...	136	mpfi	3.19	3.40	8	115	5500	18	22	17450

5 rows × 25 columns

MIのscikit-learnアルゴリズムは、離散的特徴量を連続的特徴量とは異なる方法で扱います。したがって、どれがどれであるかを伝える必要があります。経験則として、float型を持つ必要があるものは離散的ではありません。カテゴリ(オブジェクトまたはcategorial dtype)は、ラベルエンコーディングを与えることで離散的に扱うことができます。(ラベルのエンコーディングについては、カテゴリ変数のレッスンで確認できます。)

X = df.copy()
y = X.pop("price")

# Label encoding for categoricals
for colname in X.select_dtypes("object"):
    X[colname], _ = X[colname].factorize()

# All discrete features should now have integer dtypes (double-check this before using MI!)
discrete_features = X.dtypes == int

scikit-learnのfeature_selectionモジュールには、実数値ターゲット用(mutual_info_regression)と、カテゴリターゲット用(mutual_info_classif)の2つの相互情報量メトリックがあります。ターゲットである価格は実数値です。次のコードは特徴量のMIスコアを計算し、それを適切なデータフレームにまとめます。

from sklearn.feature_selection import mutual_info_regression

def make_mi_scores(X, y, discrete_features):
    mi_scores = mutual_info_regression(X, y, discrete_features=discrete_features)
    mi_scores = pd.Series(mi_scores, name="MI Scores", index=X.columns)
    mi_scores = mi_scores.sort_values(ascending=False)
    return mi_scores

mi_scores = make_mi_scores(X, y, discrete_features)
mi_scores[::3]  # show a few features with their MI scores

console

curb_weight          1.540126
highway_mpg          0.951700
length               0.621566
fuel_system          0.485085
stroke               0.389321
num_of_cylinders     0.330988
compression_ratio    0.133927
fuel_type            0.048139
Name: MI Scores, dtype: float64

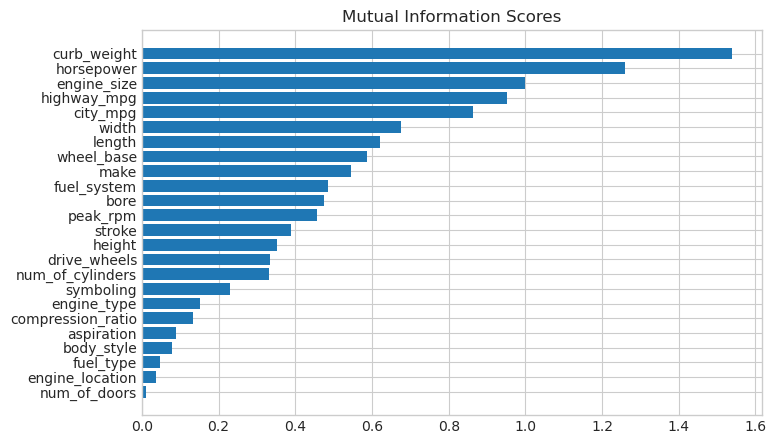
比較しやすく棒グラフにすると次の通り

def plot_mi_scores(scores):
    scores = scores.sort_values(ascending=True)
    width = np.arange(len(scores))
    ticks = list(scores.index)
    plt.barh(width, scores)
    plt.yticks(width, ticks)
    plt.title("Mutual Information Scores")


plt.figure(dpi=100, figsize=(8, 5))
plot_mi_scores(mi_scores)

データの視覚化は、ユーティリティランキングの優れたフォローアップです。いくつか詳しく見てみましょう。

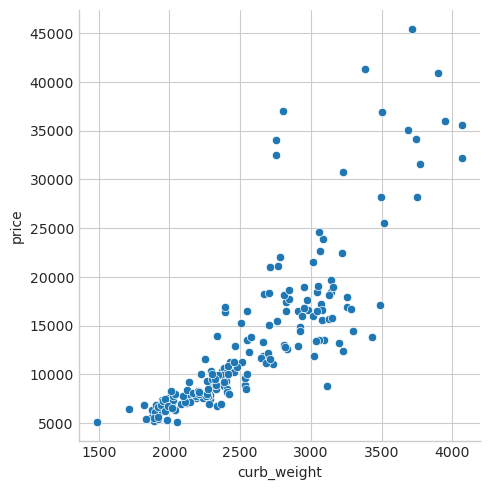
予想通り、高スコアのcurb_weightの特徴量は、ターゲットであるpriceと強い関係を示しています。

sns.relplot(x="curb_weight", y="price", data=df);

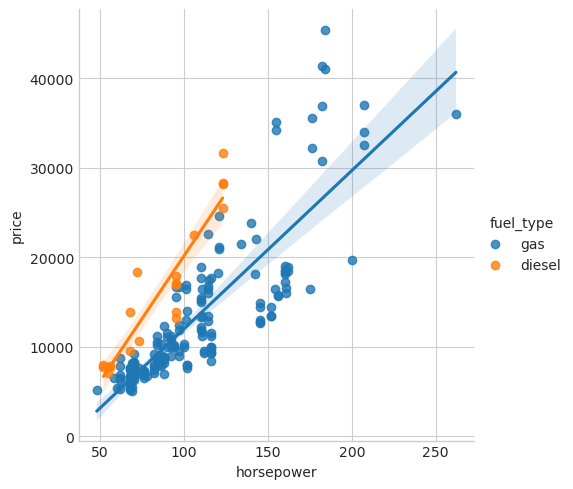
fuel_typeの特徴量のMIスコアはかなり低いですが、図からわかるように、horsepowerの特徴量で異なる傾向を持つ2つの価格集団が明確に分離されています。これは、fuel_typeが相互作用効果に寄与しており、結局は重要でないわけではないことを示しています。MIスコアから特徴量が重要でないと判断する前に、起こりうる相互作用の影響を調査することをお勧めします。ドメイン知識はここで多くのガイダンスを提供できます。

sns.lmplot(x="horsepower", y="price", hue="fuel_type", data=df);

データの視覚化は、特徴量エンジニアリングツールボックスに追加すると効果的です。相互情報量などの有用指標とともに、このような視覚化はデータ内の重要な関係を発見するのに役立ちます。詳細については、データ視覚化コースをご覧ください。