はじめに
当記事はkaggleのLearnのFeature EngineeringのPrincipal Component Analysisを翻訳して備忘としたものです。
拙い英語力なので間違い等あればご指摘いただけたらと思います。
まとめ:【kaggle】翻訳記事まとめ【備忘翻訳】
前:【kaggle】特徴量エンジニアリング - K平均法によるクラスタリング【備忘翻訳】
次:【kaggle】特徴量エンジニアリング - ターゲットエンコーディング【備忘翻訳】
当記事に含まれるコードはkaggle内のnotebook内で正常に動作します。動作を試したい場合はkaggleのnotebookで試してください。
主成分分析
バリエーションを分析することで新しい特徴量を発見します。
イントロダクション
前回のレッスンでは、特徴量エンジニアリングの最初のモデルベースであるクラスタリングについて説明しました。このレッスンでは、次の主成分分析(principal componemt analysis (PCA))について説明します。クラスタリングが近接性に基づいてデータセットを分割するのと同様に、PCAはデータ内の変動を分割するものと考えることができます。PCAは、データ内の重要な関係を発見するのに役立つ優れたツールであり、より有益な機能を作成するためにも使用できます。
(技術的メモ: PCAは通常、標準化されたデータに適用されます。標準化されたデータの場合、「変動」は「相関」を意味します。標準化されていないデータの場合、「変動」は「共分散」を意味します。このコースの全てのデータはPCAを適用する前に標準化されます。)
主成分分析
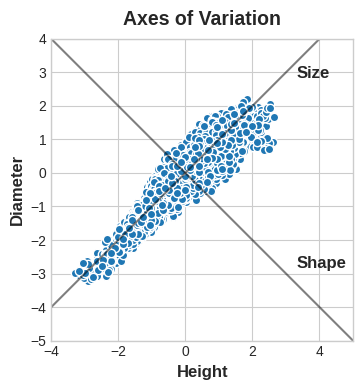
アワビのデータセットには、数千個のタスマニア産アワビから採取された物理的測定値が含まれています。ここでは、殻の「高さ」と「直径」という2つの特徴量だけを見ていきます。
このデータの中には、アワビがお互いにどのように異なる傾向があるかを説明する「変動軸」が含まれていると想像できます。図で表すと、これらの軸は、データの自然な次元に沿って走る垂直線として表示され、元の特徴量ごとに1つの軸があります。
多くの場合、これらの変化の軸に名前を付けることができます。長い軸は「Size」コンポーネントと呼ぶことができます。高さと直径が小さい(左下)のと、高さと直径が大きい(右上)のが対照的です。短い軸は「Shape」コンポーネントと呼ぶことができます。高さが小さく直径が大きい(平らな形状)のと、高さが大きく直径が小さい(丸い形状)のとが対照的です。
アワビを「Height」と「Diameter」で表現する代わりに、「Size」と「Shape」で表現することもできることに注目してください。実際、これがPCAの全体的な考え方です。データをもとの特徴量で記述するのではなく、変化の軸で記述します。変化の軸が新しい特徴になります。
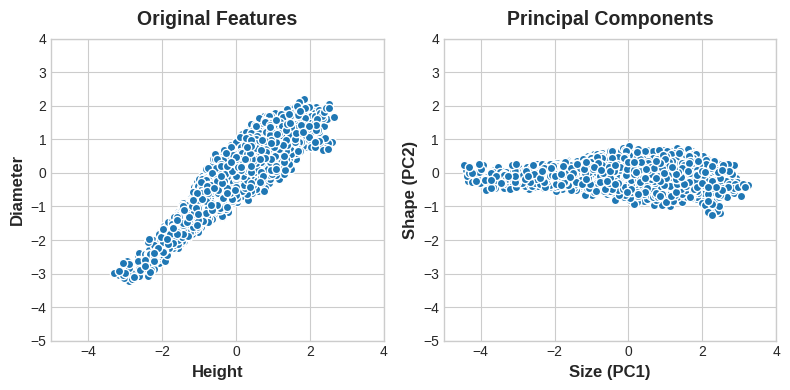
主成分は、特徴量空間内のデータセットの回転によって新しい特徴量になります。
新しい特徴量PCA構造は、実際には元の特徴量の単なる線形結合(荷重合計)です。
df["Size"] = 0.707 * X["Height"] + 0.707 * X["Diameter"]
df["Shape"] = 0.707 * X["Height"] - 0.707 * X["Diameter"]
重量そのものは
これらの新しい特徴量は、データの主成分と呼ばれます。重みそのものは負荷量(ローディング loadings) と呼ばれます。主成分の数は、元のデータセットの特徴量の数と同じになります。つまり、2つの特徴量ではなく10個の特徴量を使用した場合、主成分は10個になります。
コンポーネントの負荷量は、符号と大きさを通じてどのような変化を表現するかを示します。
| Features \ Components | Size (PC1) | Shape (PC2) |
|---|---|---|
| Height | 0.707 | 0.707 |
| Diameter | 0.707 | -0.707 |
この負荷量テーブルは、サイズコンポーネントでは高さと直径が同じ方向(同じ符号)に変化しますが、形状コンポーネントでは反対方向(異なる符号)に変化することを示しています。各コンポーネントでは、負荷量は全て同じ大きさであるため、特徴量は両方に等しく貢献します。
PCAは各コンポーネントの変動量も教えてくれます。図からShapeコンポーネントよりもSizeコンポーネントに沿ったデータの変動が大きいことが分ります。PCAは、各コンポーネントに示される分散のパーセンテージによって、正確に把握することができます。
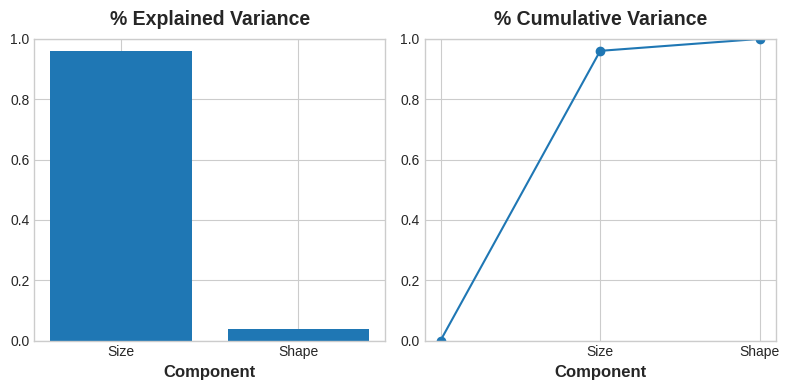
高さと直径の差異のうち、Sizeは約96%を占め、Shapeは約4%を占めます。
Sizeコンポーネントは、HightとDiameterの間の変動の大部分を捉えます。ただし、コンポーネントの分散の量は、必ずしも予測子としての精度と一致するわけではなく、何を予測しようとしているかによって異なることを覚えておくことが重要です。
特徴量エンジニアリングのためのPCA
特徴量エンジニアリングにPCAを使用する方法は2つあります。
最初の方法はそれを記述的手法として使用することです。コンポーネントは変動について教えてくだれるので、コンポーネントのMIスコアを計算して、どのような変動がターゲットを最も予測できるかを確認できます。これによって、作成する特徴量の種類に関するアイデアが得られるかもしれません--たとえば、「Size」が重要な場合は「Hight」と「Diameter」の積、形状が重要な場合は「Hight」と「Diameter」の比率などです。スコアの高いコンポーネントの1つ以上でクラスタリングを試すこともできます。
2番目の方法は、コンポーネント自体を特徴量として使用することです。コンポーネントはデータの変分構造を直接公開するため、多くの場合、元の特徴量よりも多くの情報を提供できます。次に使用例をいくつか示します:
- 次元削減: 特徴量の冗長な場合(特に多重共線性)、PCAは冗長性を1つ以上のゼロに近い分散コンポーネントへ分割します。これらのコンポーネントには情報がほとんど含まれないため、削除できます。
- 異常検出: 元の特徴量からは明らかでない異常な変動は、多くの場合、鄭文さんコンポーネントに現れます。これらのコンポーネントは、異常またははずれ値検出タスクで非常に有益です。
- ノイズ低減: センサー読み取りの値の集合は、多くの場合、共通の背景ノイズを共有します。PCAは、ノイズをそのままにしながら(有益な)信号をより少数の特徴量に集めることができるため、信号対ノイズ比を高めることができます。
- 無相関: 一部のMLアルゴリズムは、相関性の高い特徴量の処理に苦労します。PCAは相関のある特徴量を相関のないコンポーネントに変換します。これにより、アルゴリズムが処理しやすくなります。
PCAは基本的に、データの相関構造に直接アクセスできるようにします。きっと、独自のアプリケーションが思いつくでしょう!
例 - 1985年自動車
この例では、自動車データセットに戻り、PCAを特徴量を発見するための記述的手法として使用して適用します。演習では、他のユースケースも見ていきます。
以下の折り畳み部分はデータを読み込み、関数plot_varianceとmake_mi_scoreを定義します。
setup
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns
from IPython.display import display
from sklearn.feature_selection import mutual_info_regression
plt.style.use("seaborn-whitegrid")
plt.rc("figure", autolayout=True)
plt.rc(
"axes",
labelweight="bold",
labelsize="large",
titleweight="bold",
titlesize=14,
titlepad=10,
)
def plot_variance(pca, width=8, dpi=100):
# Create figure
fig, axs = plt.subplots(1, 2)
n = pca.n_components_
grid = np.arange(1, n + 1)
# Explained variance
evr = pca.explained_variance_ratio_
axs[0].bar(grid, evr)
axs[0].set(
xlabel="Component", title="% Explained Variance", ylim=(0.0, 1.0)
)
# Cumulative Variance
cv = np.cumsum(evr)
axs[1].plot(np.r_[0, grid], np.r_[0, cv], "o-")
axs[1].set(
xlabel="Component", title="% Cumulative Variance", ylim=(0.0, 1.0)
)
# Set up figure
fig.set(figwidth=8, dpi=100)
return axs
def make_mi_scores(X, y, discrete_features):
mi_scores = mutual_info_regression(X, y, discrete_features=discrete_features)
mi_scores = pd.Series(mi_scores, name="MI Scores", index=X.columns)
mi_scores = mi_scores.sort_values(ascending=False)
return mi_scores
df = pd.read_csv("../input/fe-course-data/autos.csv")
様々なプロパティをカバーする4つの特徴量を選択しました。これらの特徴量はそれぞれ、ターゲットであるPliceに対して高いMIスコアを持っています。これらの特徴量は本来同じスケールではないため、データを標準化します。
features = ["highway_mpg", "engine_size", "horsepower", "curb_weight"]
X = df.copy()
y = X.pop('price')
X = X.loc[:, features]
# Standardize
X_scaled = (X - X.mean(axis=0)) / X.std(axis=0)
これで、scikit-learnのPCA推定量にfitし、主成分を作成することができます。ここで、変換されたデータセットの最初の数行を確認します。
from sklearn.decomposition import PCA
# Create principal components
pca = PCA()
X_pca = pca.fit_transform(X_scaled)
# Convert to dataframe
component_names = [f"PC{i+1}" for i in range(X_pca.shape[1])]
X_pca = pd.DataFrame(X_pca, columns=component_names)
X_pca.head()
| PC1 | PC2 | PC3 | PC4 | |
|---|---|---|---|---|
| 0 | 0.382486 | -0.400222 | 0.124122 | 0.169539 |
| 1 | 0.382486 | -0.400222 | 0.124122 | 0.169539 |
| 2 | 1.550890 | -0.107175 | 0.598361 | -0.256081 |
| 3 | -0.408859 | -0.425947 | 0.243335 | 0.013920 |
| 4 | 1.132749 | -0.814565 | -0.202885 | 0.224138 |
fitting後、PCAインスタンスのcomponents_属性に負荷量が含まれます。(残念ながらPCAの用語は一貫していません。X_pca内の変換された列をコンポーネントと呼ぶ規則に従っていますが、それ以外には名前がありません)読み込みデータをデータフレームにまとめます。
loadings = pd.DataFrame(
pca.components_.T, # transpose the matrix of loadings
columns=component_names, # so the columns are the principal components
index=X.columns, # and the rows are the original features
)
loadings
| PC1 | PC2 | PC3 | PC4 | |
|---|---|---|---|---|
| highway_mpg | -0.492347 | 0.770892 | 0.070142 | -0.397996 |
| engine_size | 0.503859 | 0.626709 | 0.019960 | 0.594107 |
| horsepower | 0.500448 | 0.013788 | 0.731093 | -0.463534 |
| curb_weight | 0.503262 | 0.113008 | -0.678369 | -0.523232 |
コンポーネントの負荷量の符号と大きさから、どのような変動が補足されているかが分かることを思い出してください。最初のコンポーネント(PC1)は、燃費の悪い大型でパワフルな自動車と、燃費のいい小型で経済的な自動車との対比を示しています。これを「ラグジュアリー/エコノミー」軸と呼ぶこともできます。次の図は、選択した4つの特徴量が主にラグジュアリー/エコノミー軸に沿って変化していることを示しています。
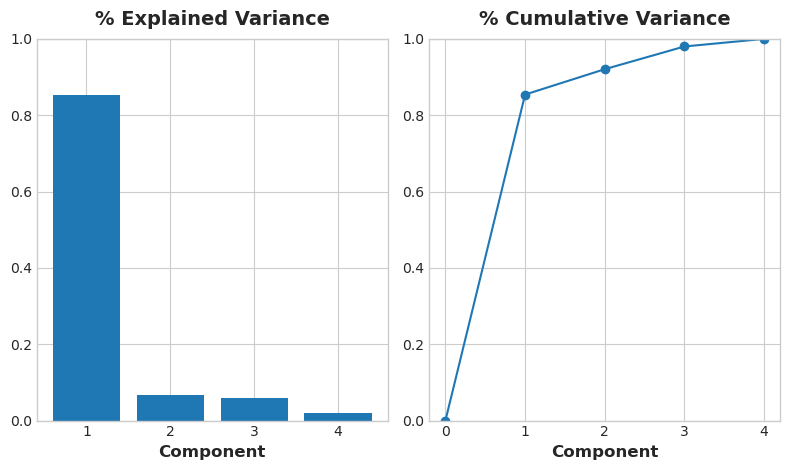
# Look at explained variance
plot_variance(pca);
コンポーネントのMIスコアも見てみましょう。予想通り、PC1は非常に有益ですが、残りのコンポーネントは、小さな変動にも関わらず、Priceと有意な関連を持っている。ラグジュアリー/エコノミー軸では捉えきれない関係を見つけるために、これらのコンポーネントを調べる価値があるかもしれません。
mi_scores = make_mi_scores(X_pca, y, discrete_features=False)
mi_scores
PC1 1.013264
PC2 0.379156
PC3 0.306703
PC4 0.203329
Name: MI Scores, dtype: float64
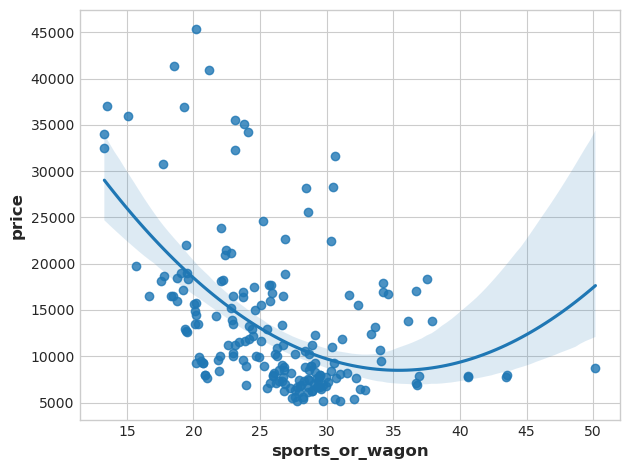
3番目の要素は、horsepoowerとcurb_weightの対比を示しています。スポーツカーとワゴンのようです。
# Show dataframe sorted by PC3
idx = X_pca["PC3"].sort_values(ascending=False).index
cols = ["make", "body_style", "horsepower", "curb_weight"]
df.loc[idx, cols]
| make | body_style | horsepower | curb_weight | |
|---|---|---|---|---|
| 118 | porsche | hardtop | 207 | 2756 |
| 117 | porsche | hardtop | 207 | 2756 |
| 119 | porsche | convertible | 207 | 2800 |
| 45 | jaguar | sedan | 262 | 3950 |
| 96 | nissan | hatchback | 200 | 3139 |
| ... | ... | ... | ... | ... |
| 59 | mercedes-benz | wagon | 123 | 3750 |
| 61 | mercedes-benz | sedan | 123 | 3770 |
| 101 | peugot | wagon | 95 | 3430 |
| 105 | peugot | wagon | 95 | 3485 |
| 143 | toyota | wagon | 62 | 3110 |
193 rows × 4 columns
このコントラストを表現するために、新しい特徴量の比率を作成しましょう。
df["sports_or_wagon"] = X.curb_weight / X.horsepower
sns.regplot(x="sports_or_wagon", y='price', data=df, order=2);