はじめに
当記事はkaggleのLearnのIntro to Machine LearningのBar Charts and Heatmapsを翻訳して備忘としたものです。
拙い英語力なので間違い等あればご指摘いただけたらと思います。
まとめ:【kaggle】翻訳記事まとめ【備忘翻訳】
前:【kaggle】データの視覚化 - 折れ線グラフ【備忘翻訳】
次:【kaggle】データの視覚化 - 分布【備忘翻訳】
当記事に含まれるコードはkaggle内のnotebook内で正常に動作します。動作を試したい場合はkaggleのnotebookで試してください。
散布図
座標平面を活用して変数間の関係を調べる。
このチュートリアルでは高度な散布図を作成する方法を学びます。
notebookのセットアップ
いつものように、コーディング環境の設定から始めます。
set up
import pandas as pd
pd.plotting.register_matplotlib_converters()
import matplotlib.pyplot as plt
%matplotlib inline
import seaborn as sns
print("Setup Complete")
Setup Complete
データのロードと調査
保険料の(合成)データセットを用いて、一部の顧客が他の顧客よりも高い保険料を支払う理由を理解できるかどうかを確認します。
時間があれば、データセットの詳細をこちらからお読みください。
# Path of the file to read
insurance_filepath = "../input/insurance.csv"
# Read the file into a variable insurance_data
insurance_data = pd.read_csv(insurance_filepath)
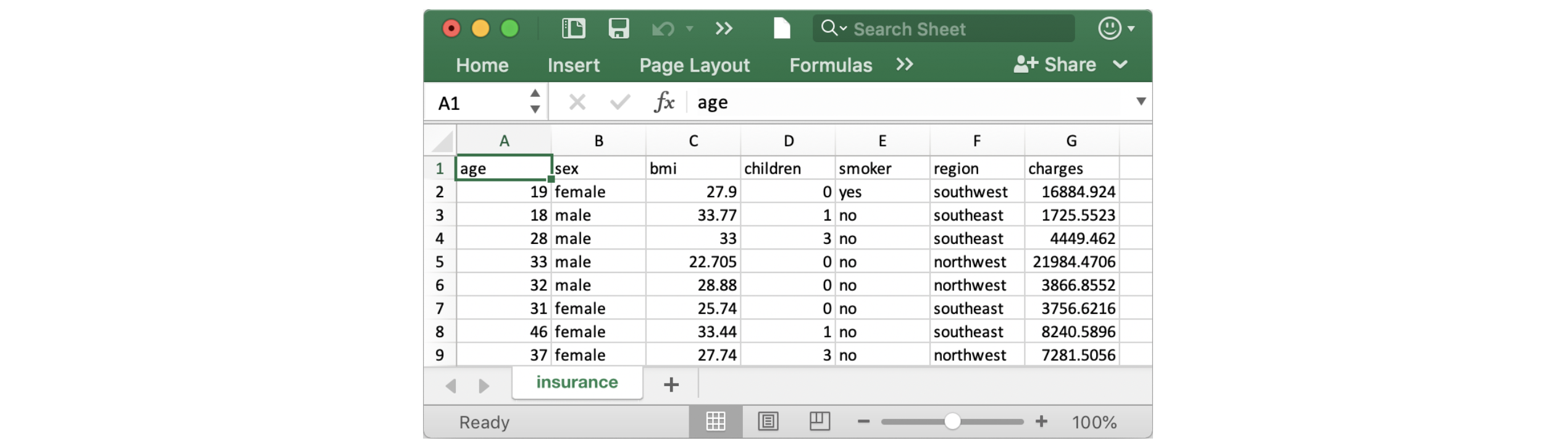
いつものように最初の5行を表示してデータセットが適切に読み込まれたかどうかを確認しましょう。
insurance_data.head()
| age | sex | bmi | children | smoker | region | charges | |
|---|---|---|---|---|---|---|---|
| 0 | 19 | female | 27.900 | 0 | yes | southwest | 16884.92400 |
| 1 | 18 | male | 33.770 | 1 | no | southeast | 1725.55230 |
| 2 | 28 | male | 33.000 | 3 | no | southeast | 4449.46200 |
| 3 | 33 | male | 22.705 | 0 | no | northwest | 21984.47061 |
| 4 | 32 | male | 28.880 | 0 | no | northwest | 3866.85520 |
散布図
単純な散布図を作成するには、sns.scatterplotコマンドを使用して次の引数を指定します。
- 水平軸 X軸 (
x=insurance_data['bmi'])と、 - 垂直軸 Y軸(
y=insurance_data['charges'])
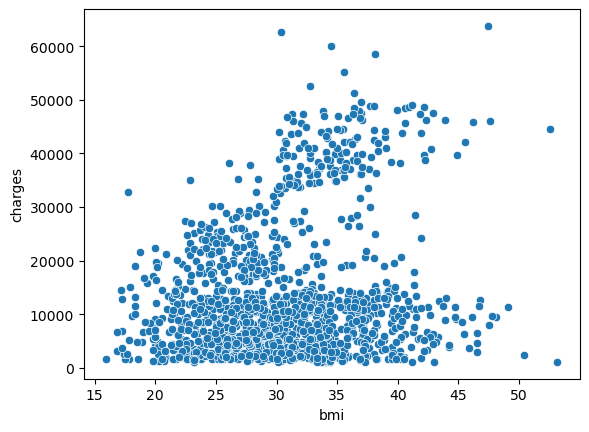
sns.scatterplot(x=insurance_data['bmi'], y=insurance_data['charges'])
<AxesSubplot:xlabel='bmi', ylabel='charges'>
上記の散布図は、ボディマス指数(BMI)と保険料が正の相関関係があり、BMIが高い顧客は通常、保険料も高くなる傾向があることを示唆しています。(この相関関係は理にかなっています。なぜなら、BMIが高いと、一般に慢性疾患のリスクが高くなるからです。)
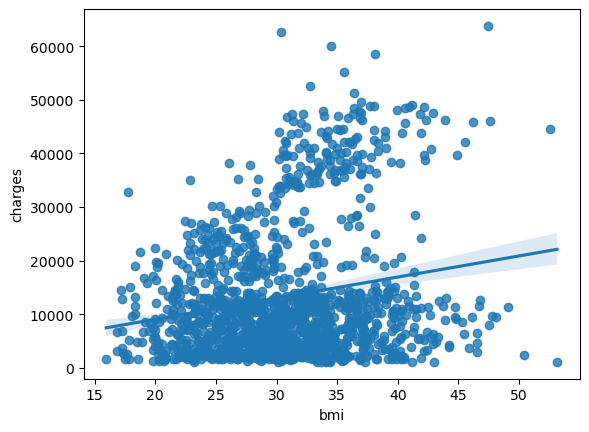
この相関関係の強さを再確認するには、回帰線、つまりデータに最も適合する線を追加すると良いでしょう。これを実現するコマンドである、sns.regplotに変更します。
sns.regplot(x=insurance_data['bmi'], y=insurance_data['charges'])
<AxesSubplot:xlabel='bmi', ylabel='charges'>
色分けされた散布図
散布図を使用すると、(2つではなく)3つの変数間の関係を表示できます。これを行う方法は、ポイントを色分けすることです。
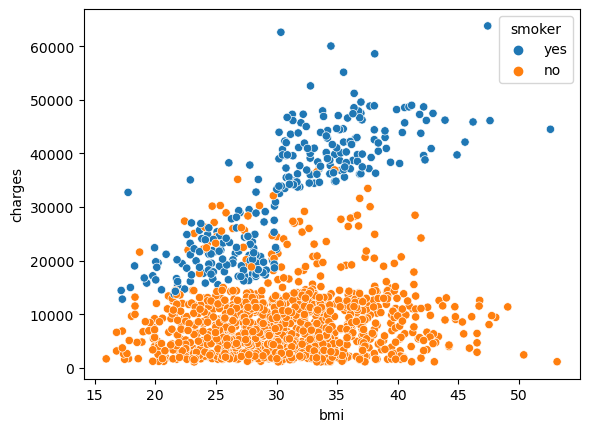
例えば、喫煙がBMIと保険料の関係にどのように影響するかを理解するために、ポイントを「喫煙者」ごとに色分けし、他の2つの列(「BMI」、「料金」)を軸にプロットすることができます。
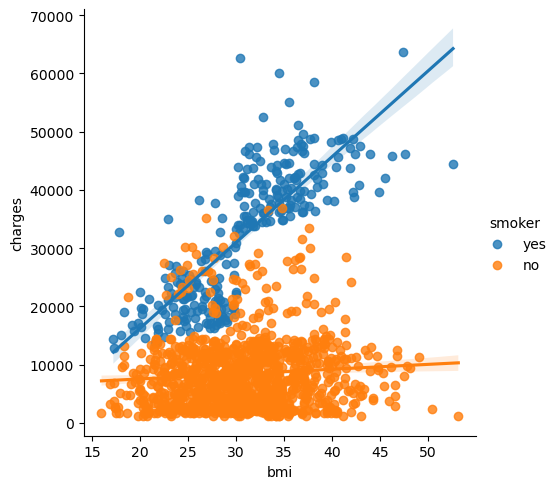
sns.scatterplot(x=insurance_data['bmi'], y=insurance_data['charges'], hue=insurance_data['smoker'])
<AxesSubplot:xlabel='bmi', ylabel='charges'>
この散布図は、非喫煙者はBMIが増加するにつれて支払う金額がわずかに増加する傾向があるのに対し、喫煙者ははるかに多く支払う傾向があることを示しています。
この事実をさらに強調するために、sns.Implotコマンドを使用して、喫煙者と非喫煙者に対応する2つの回帰線を追加できます。(喫煙者の回帰線は、非喫煙者の線に比べて、はるかに急な傾きになっていることに気付くでしょう。)
sns.lmplot(x="bmi", y="charges", hue="smoker", data=insurance_data)
<seaborn.axisgrid.FacetGrid at 0x7c1b45c4d510>
上記のsns.Implotコマンドは、これまで学習したコマンドとは少し異なる動作をします。
-
insurance_dataの'BMI'列を選択するためにx=insuranxe_data['BMI']を設定する代わりに、列の名前のみを指定するためにx="BMI"を設定します。 - 同様に
y="charges"とhue="Smoker"にも列の名前が含まれています。 - データセットは、
data=insurance_dataで指定します。
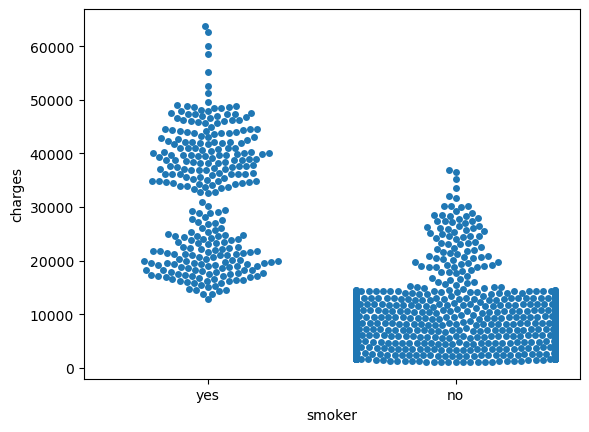
最後に、もう1つ学ぶプロットがあります。これは、散布図で見慣れているものとは少し異なるかもしれません。通常、散布図は、2つの連続変数(「bmi」と「料金」など)の関係を強調するために使用します。しかし、散布図のデザインを適応させて、カテゴリ変数(「喫煙者」のような)を主軸の1つにフィーチャーすることができます。このプロットタイプをカテゴリー散布図と呼び、sns.swarplotコマンドで作成します。
sns.swarmplot(x=insurance_data['smoker'],
y=insurance_data['charges'])
/opt/conda/lib/python3.7/site-packages/seaborn/categorical.py:3544: UserWarning: 37.4% of the points cannot be placed; you may want to decrease the size of the markers or use stripplot.
warnings.warn(msg, UserWarning)
<AxesSubplot:xlabel='smoker', ylabel='charges'>
/opt/conda/lib/python3.7/site-packages/seaborn/categorical.py:3544: UserWarning: 60.8% of the points cannot be placed; you may want to decrease the size of the markers or use stripplot.
warnings.warn(msg, UserWarning)
このグラフから、次のことが分ります。
- 平均すると非喫煙者は喫煙者よりも料金が安く、
- 最も多く支払う人は喫煙者であり、最も少なく支払う人は非喫煙者です。