はじめに
オセロAdvent Calendarも22日目になりました。残すところあとわずかですね。
本記事ではオセロソフトEdaxの評価関数について書きます。前々からEdaxの評価関数については気になっていて調べてみたかったのですが、読み解くのが難しく挫折していました。今回、Advent Calendarという機会をいただいて頑張って解読してみたので、その結果を書くことにしました。
注:本記事で紹介しているEdax(edax-reversi)はRichard Delorme氏によるGPL v3ソフトウェアです。ソースコードは以下に公開されています。
https://github.com/abulmo/edax-reversi
では、評価関数の仕組みを探る長い長い旅に出発しましょう!
この記事を読むとわかる(はずの)こと
- Edaxの評価関数の求め方
- eval.datファイルは何なのか
この記事を読んでもわからないこと
- 評価関数から評価値を求めるに当たっての探索関連の手法
- eval.datファイルの作り方
- bookについて
- オセロの真理
ここで少し補足をしておきます。
評価値を算出する際には、評価関数と探索というものが関連してきます。評価関数というのは、細かい話はWikipediaの記事に譲りますが、ものすごく大雑把に言えばある盤面がパッと見どちらがどれくらい有利かを表す指標です。
オセロにおいては「どちらがどれくらい有利か」は、最終的に自分が何石差で勝つ/負けるくらいの形勢差があるかで表されていて、プラスだと手番側が有利、マイナスだと手番側が不利ということを意味しています。
また「パッと見」という言葉を使ったのはそれなりに意味があって、その盤面から1手も先読みをしないで判断する、ということを表しています。Wikipediaの記事に「静的に」評価すると書かれているのはそういう意味です。
1手も先読みしないで大丈夫なのかという疑問を持たれた方、ここが探索の出番で、探索が先読みする役割を担っており、先読みした先の局面について評価関数で求めた値を元に現局面においてどの手が最善かという評価値を算出しています。オセロアプリなどで表示されている着手ごとの評価値はこのように算出した値です。
このあたりの詳しい話については、5分で覚えるAI Minimax(ミニマックス)法とalpha-beta法という記事を見つけたので興味のある方はそちらをご参照ください。
本記事では冒頭でも書いたように探索については扱わず、評価関数のみ、しかもEdaxの評価関数についてのみを扱います。
これがEdaxの評価関数だ!
話はいきなり核心に迫ります。Edaxの評価関数はmidgame.cというファイルのsearch_eval_0で定義されています。
int search_eval_0(Search *search)
{
const short *w = EVAL_WEIGHT[search->eval->player][60 - search->n_empties];
int *f = search->eval->feature;
int score;
SEARCH_STATS(++statistics.n_search_eval_0);
SEARCH_UPDATE_EVAL_NODES();
score = w[f[ 0]] + w[f[ 1]] + w[f[ 2]] + w[f[ 3]]
+ w[f[ 4]] + w[f[ 5]] + w[f[ 6]] + w[f[ 7]]
+ w[f[ 8]] + w[f[ 9]] + w[f[10]] + w[f[11]]
+ w[f[12]] + w[f[13]] + w[f[14]] + w[f[15]]
+ w[f[16]] + w[f[17]] + w[f[18]] + w[f[19]]
+ w[f[20]] + w[f[21]] + w[f[22]] + w[f[23]]
+ w[f[24]] + w[f[25]]
+ w[f[26]] + w[f[27]] + w[f[28]] + w[f[29]]
+ w[f[30]] + w[f[31]] + w[f[32]] + w[f[33]]
+ w[f[34]] + w[f[35]] + w[f[36]] + w[f[37]]
+ w[f[38]] + w[f[39]] + w[f[40]] + w[f[41]]
+ w[f[42]] + w[f[43]] + w[f[44]] + w[f[45]]
+ w[f[46]];
if (score > 0) score += 64; else score -= 64;
score /= 128;
if (score <= SCORE_MIN) score = SCORE_MIN + 1;
else if (score >= SCORE_MAX) score = SCORE_MAX - 1;
return score;
}
いきなり核心すぎて意味がわからないですが、0〜46までの何かの値を足しているのが見て取れます。その後の部分は正なら64を加算、負なら64を減算して128で割った商(整数)を求めているので、要するに元の値を128で割って四捨五入しているということになります。どうやらEdaxの内部では例えば合計値が1280なら評価値は+10というように、128倍のスケールになっている値を合計してから128で割っているようです。そのあとのSCORE_MINやSCORE_MAXのあたりは、プラスマイナス64の範囲に収まるように頭打ちにしている処理です。
なので、評価関数の本質は0〜46までの謎の値(特徴量)の加算部分になります。ここで使われているwやfは関数冒頭で定義されていて、それぞれEVAL_WEIGHTとsearch->eval->featureというものに由来していることがわかります。これらが何を意味しているかについて調べてみましょう。
featureとは何なのか
featureの値は以下で設定されています。
void eval_set(Eval *eval, const Board *board)
{
int i, j, c;
for (i = 0; i < EVAL_N_FEATURE; ++i) {
eval->feature[i] = 0;
for (j = 0; j < EVAL_F2X[i].n_square; j++) {
c = board_get_square_color(board, EVAL_F2X[i].x[j]);
eval->feature[i] = eval->feature[i] * 3 + c;
}
eval->feature[i] += EVAL_OFFSET[i];
}
eval->player = 0;
}
厳密に言えば、ある局面の評価値を求める際にその局面の時点(探索を開始する時点)でこのeval_setを実行してfeatureを設定し、先読み探索中は変更箇所をeval_update_0等で更新しているという動きをしているのですが、意味を理解する上ではeval_setがわかれば良いので、こちらを見てみることにします。
二重ループになっていますが、外側のEVAL_N_FEATUREの値は47なので、この外側のループで0〜46の47個分の処理をしていることがわかります。それぞれのfeatureの値を0に初期化した後、内側のループで何やらboard_get_square_colorの値を加えては3倍するということを繰り返して、最後に何かのオフセット値を加算しています。この内側のループの核心になっているのがEVAL_F2Xという配列で、以下のように定義されています。
static const FeatureToCoordinate EVAL_F2X[] = {
{ 9, {A1, B1, A2, B2, C1, A3, C2, B3, C3}},
{ 9, {H1, G1, H2, G2, F1, H3, F2, G3, F3}},
{ 9, {A8, A7, B8, B7, A6, C8, B6, C7, C6}},
{ 9, {H8, H7, G8, G7, H6, F8, G6, F7, F6}},
//(以下略)
棋譜の座標が出てきました。実際には47個分の定義があるのですが、まずは冒頭の4つだけ引用しました。最初の1行で定義されているのはA1〜C3までの左上隅9マスの座標になっています。以下の図はA1〜C3まで登場順に番号を振ったものです。
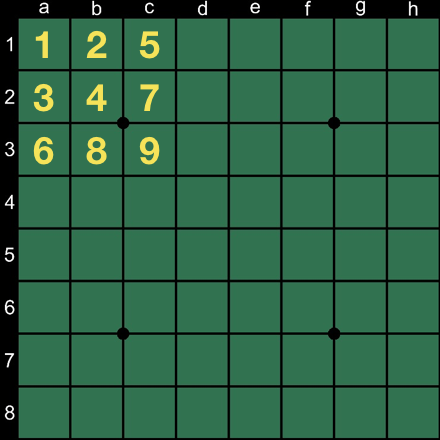
2〜4行目の座標は、右上、左下、右下で、上記の隅9マスの対称形を定義しています。「以下略」と書いた5行目以降も俄然気になってきますが、そこはこの後の楽しみに取っておくとして、話を先に進めます。
上記の定義を踏まえて、もう一度eval_setを読み直してみると、例えばfeature[0]というのはこの9マスについて順番にboard_get_square_colorでマスの石の色を取得して、3倍しながら加えていっているように見えます。
実際、board.cのboard_get_square_colorという関数には以下のようなコメントが書かれており、自プレーヤー(その局面で手番側のプレーヤー)の石の場合は0、相手側の石の場合は1、空きマスの場合は2を返すということが書かれています。
/**
* @brief Get square color.
*
* returned value: 0 = player, 1 = opponent, 2 = empty;
*
* @param board board.
* @param x square coordinate.
* @return square color.
*/
この値を3倍しながら足していっているということは、要するに9マス分これらの値を221021002のように並べた値を3進数として解釈した値、ということになります。先ほどの左上隅9マスで言えば、A1が3^8=6561の位、B1が3^7=2187の位、...、C3が3^0=1の位という具合です。
なので、この値は値の大きさにはあまり意味がなく、純粋に9マス分の範囲の石の配置パターンに一意の番号を振ったものだと思えば良さそうです。
このような値をEVAL_F2Xに定義された全47個のfeatureについて求めてfeature[i]に代入しています。最後に加算しているオフセットについては、後ほど説明します。
EVAL_WEIGHTとは何なのか
featureの意味が大体わかったので、もう1つのポイントであったEVAL_WEIGHTについても調べてみましょう。これの核心部分はeval.cのeval_openという関数です。この関数はやや長いですが、細かい部分は省略して骨格だけ抜粋してみたいと思います。エラー処理等は省略しています。Step 1〜4やところどころにある日本語のコメントは筆者が入れたものです。
void eval_open(const char* file)
{
const int n_w = 114364;
int *T;
int ply, i, j, k, l, n;
int r;
int offset;
FILE* f;
short *w = NULL;
// create unpacking tables ***Step1***
T = (int*) malloc(59049 * sizeof (*T));
// (筆者注:この前後、以下と同様の処理多数)
for (l = n = 0;l < 19683; l++) { /* 9 corner squares : 19683 -> 10206 */
k = ((l / 6561) % 3) * 6561 + ((l / 729) % 3) * 2187 +
((l / 2187) % 3) * 729 + ((l / 243) % 3) * 243 +((l / 27) % 3) * 81 +
((l / 81) % 3) * 27 + ((l / 3) % 3) * 9 + ((l / 9) % 3) * 3 + (l % 3);
if (k < l) T[l] = T[k];
else T[l] = n++;
EVAL_C9[0][l] = T[l];
EVAL_C9[1][opponent_feature(l, 9)] = T[l];
}
free(T);
// (筆者注:この前後、以下と同様の処理多数)
// allocation ***Step2***
EVAL_WEIGHT = (short***) malloc(2 * sizeof (*EVAL_WEIGHT));
EVAL_WEIGHT[0] = (short**) malloc(2 * EVAL_N_PLY * sizeof (**EVAL_WEIGHT));
EVAL_WEIGHT[1] = EVAL_WEIGHT[0] + EVAL_N_PLY;
EVAL_WEIGHT[0][0] = (short*) malloc(2 * EVAL_N_PLY * EVAL_N_WEIGHT * sizeof (***EVAL_WEIGHT));
EVAL_WEIGHT[1][0] = EVAL_WEIGHT[0][0] + EVAL_N_PLY * EVAL_N_WEIGHT;
for (ply = 1; ply < EVAL_N_PLY; ply++) {
EVAL_WEIGHT[0][ply] = EVAL_WEIGHT[0][ply - 1] + EVAL_N_WEIGHT;
EVAL_WEIGHT[1][ply] = EVAL_WEIGHT[1][ply - 1] + EVAL_N_WEIGHT;
}
// data reading ***Step3***
w = (short*) malloc(n_w * sizeof (*w)); // a temporary to read packed weights
f = fopen(file, "rb");
// (筆者注:ファイルヘッダ読み込み処理(省略))
// Weights : read & unpacked them ***Step4***
for (ply = 0; ply < EVAL_N_PLY; ply++) {
r = fread(w, sizeof (short), n_w, f);
i = j = offset = 0;
for (k = 0; k < EVAL_SIZE[i]; k++,j++) {
EVAL_WEIGHT[0][ply][j] = w[EVAL_C9[0][k] + offset];
EVAL_WEIGHT[1][ply][j] = w[EVAL_C9[1][k] + offset];
}
offset += EVAL_PACKED_SIZE[i];
// (筆者注:この後、上記と同様の処理多数)
}
fclose(f);
free(w);
}
大まかに4つのパートに分かれているので、順に説明していきます。
Step1. unpacking tableの生成
まず変数Tが59049個分のサイズをmallocしていますが、ここでは値の意味は無視して、余裕を持って大きめに領域を取ったものと思ってください。(実際には、一部処理を省略した部分で最大59049個分の領域が必要になるため、このサイズ定義になっています。引用した範囲では19683で十分です)
その次のfor文でコメントに"9 corner squares"とあり、しかも$19683=3^9$なので、先ほど図解で示した隅9マスの部分と関係しそうです。
19683回ループする中で、kの値を算出していますが、これは何でしょうか?3の冪(1,3,9,27,81,243,729,2187,6561)で割って、3の剰余を求めているのは3進数のそれぞれの桁の値を出していることになります。それをまた3の冪で掛けて足していますが、掛ける値が729と2187、27と81、3と9で入れ替わっています。つまり3進数でこれらの桁を入れ替えた値を求めていることになります。対応関係をよく見ると、実は先ほど図を出した隅9マスのfeatureで、対角線(ホワイトライン)に対して対称移動した値を表しています。意味ありげですね。
その後のif文がまたわかりにくいですが、lの方がkより小さい場合は出てきた順番に番号を振っていて、lの方が大きい場合は既に振られている対称形側の番号を代入しています。つまり、nの値は対称形同士を同一視した場合に、異なるものが出現した回数だけインクリメントします。
試しに隅9マスで異なるものが何通りあるかを求めてみましょう。全体で3^9通りあり、対角線対称なもの同士を同一視するので大体半分になるわけですが、B1=A2、C1=A3、C2=B3の条件を満たすものは対称移動しても自分自身になってしまうので、これら以外のものを半分にして、最後にこの自分自身と対称形のものを足す必要があります。結果、$(3^9 - 3^6) / 2 + 3^6 = 10206$通り存在することになります。コメントに書いてあった"19683 -> 10206"というのはこのことです。
EVAL_C9[0][l]にこの値を入れているので、l=0,1,...,19682に対して、対称形を同一視した番号である0,...,10205に変換するテーブルを作ったことになります。
opponent_featureというのは、ソースの紹介は省略しますが3進数の各位に対して0と1を入れ替える関数になっています。名前からも推測がつきますが、相手側から見た場合のfeatureの値を求める関数になります。EVAL_C9[1][opponent_feature(l,8)]にEVAL_C9[0][l]と同じ値を代入していることから、配列の1つ目の次元になっている0と1は自分から見た場合と相手から見た場合を表していることになります。
Step2. メモリの確保
続いて、EVAL_WEIGHT用のメモリ領域を確保しています。実質的には2 * EVAL_N_PLY * EVAL_N_WEIGHT * sizeof (***EVAL_WEIGHT)の部分で確保していますが、ここで使用されている定数の値は、EVAL_N_PLY = 61、EVAL_N_WEIGHT = 226315となっています。***EVAL_WEIGHTはshortなので、short用の領域を2 * 61 * 226315個分確保したことになります。
この個数の意味は何でしょうね?後から出てくるので、まずは先に進みましょう。
Step3. ファイルの読み込み
ファイル名が変数になっていて何を読み込んでいるのかこのソースからだけでは分かりませんが、ここで読んでいるのがeval.datというファイルです。
ヘッダ読み込み処理はソースコードを省略しましたが、合計28バイト分のヘッダ部があります。
Step4. ファイル内容の展開
いよいよ実際にEVAL_WEIGHTを構築している部分です。まずfor文があり、EVAL_N_PLY = 61回ループするようになっています。値や変数名からも想像がつく通り、0手目の局面から60手目の局面まで61回のループになっています。
このループの中でn_w = 114364個のshort値を読み込んでいます。そして先ほどStep1で構築した変換テーブルEVAL_C9を使い、EVAL_WEIGHT[0][ply][j]に、読み込んだ値のEVAL_C9[0][j]番目(EVAL_C9を読む場合はj=kで、offset=0なので。)の値を設定しています。
この意味は、eval.datには隅9マスの各パターンに対応する値が対称形を省略して格納されていて、その省略されている対称形を復元しながら設定している、ということです。
引用したソースではEVAL_C9で隅9マスの値を読み込む部分だけですが、「この後、上記と同様の処理多数」と書かれている部分で同じようにいろいろなパターンの値を展開して読み込んでいます。
どれだけ読み込んでいるかに関係する定義値を見てみましょう。
/** feature size */
static const int EVAL_SIZE[] = {19683, 59049, 59049, 59049, 6561, 6561, 6561, 6561, 2187,729, 243, 81, 1};
/** packed feature size */
static const int EVAL_PACKED_SIZE[] = {10206, 29889, 29646, 29646, 3321, 3321, 3321, 3321, 1134, 378, 135, 45, 1};
EVAL_SIZEはkのループの回数になっていて、すべて合計すると226315になり、EVAL_N_WEIGHTの値と一致していることがわかります。EVAL_PACKED_SIZEは対称形を省略した場合の各パターンのサイズで、合計すると114364になり、こちらはn_wの値と一致します。
今構築しているEVAL_WEIGHTは3次元の配列になっていますが、1つ目の次元が自分から見たものか相手から見たものかの0 or 1で2通り、2つ目の次元が何手目の局面かの61通り、3つ目の次元がどのパターンに対するものかで19683+59049+...+1=226315通りで、それぞれに対してshortの値を持っているので、Step3で割り当てたメモリ領域のサイズと一致していることがわかります。
さらに言えば、この読み込み元である展開前のファイルに必要なサイズは、何手目の局面かが61通りあり、それぞれに10206+29889+...+1=114364個のshort(2バイト)の値が必要なので、611143642=13952408バイトになります。eval.datのファイルサイズをみると13952436バイトとなっており、上記のサイズにファイルヘッダの28バイト分を加えた値になっていることがわかります。
つまり評価関数の実態は?
ここで改めてこの式に戻ってみましょう。
score = w[f[ 0]] + w[f[ 1]] + w[f[ 2]] + w[f[ 3]]
+ w[f[ 4]] + w[f[ 5]] + w[f[ 6]] + w[f[ 7]]
+ w[f[ 8]] + w[f[ 9]] + w[f[10]] + w[f[11]]
+ w[f[12]] + w[f[13]] + w[f[14]] + w[f[15]]
+ w[f[16]] + w[f[17]] + w[f[18]] + w[f[19]]
+ w[f[20]] + w[f[21]] + w[f[22]] + w[f[23]]
+ w[f[24]] + w[f[25]]
+ w[f[26]] + w[f[27]] + w[f[28]] + w[f[29]]
+ w[f[30]] + w[f[31]] + w[f[32]] + w[f[33]]
+ w[f[34]] + w[f[35]] + w[f[36]] + w[f[37]]
+ w[f[38]] + w[f[39]] + w[f[40]] + w[f[41]]
+ w[f[42]] + w[f[43]] + w[f[44]] + w[f[45]]
+ w[f[46]];
fがfeature、wがEVAL_WEIGHT[player][ply]のことでした。f[0]は、左上隅9マスの石の配置がどのようになっているかを表す番号で、EVAL_WEIGHTはeval.datから各パターンに対応する値を読み込んで展開した値でした。つまりeval.datには何手目かの手番ごとに石の配置パターンに対応するスコアが書かれていて、例えばw[f[0]]というのは左上隅9マスの配置だけをみたときのスコアを表していることになります。このように、盤面の一部の状況(feature)だけをみたスコアを、0〜46の47個分のfeatureについて足した値(を128で割ったもの)が評価関数の正体になります。
ということは、この47個のfeatureが何かがわかれば、Edaxが何をみて評価値を出しているのかがわかることになります。大分前の方で勿体ぶって楽しみにとっておくことにしたEVAL_F2Xの「以下略」としていた部分です。
Edaxの評価関数は盤面をこのように見ている!
いよいよ、その47個のfeatureに迫ります。47個と言いましたが、隅9マスが左上、右上、左下、右下と4種類あったように、対称となるパターンがあるので、対象形を1つと数えると実質的には13パターンになります。では、一挙公開します。それぞれの名称は筆者が勝手に名付けたものですのでご了承ください。
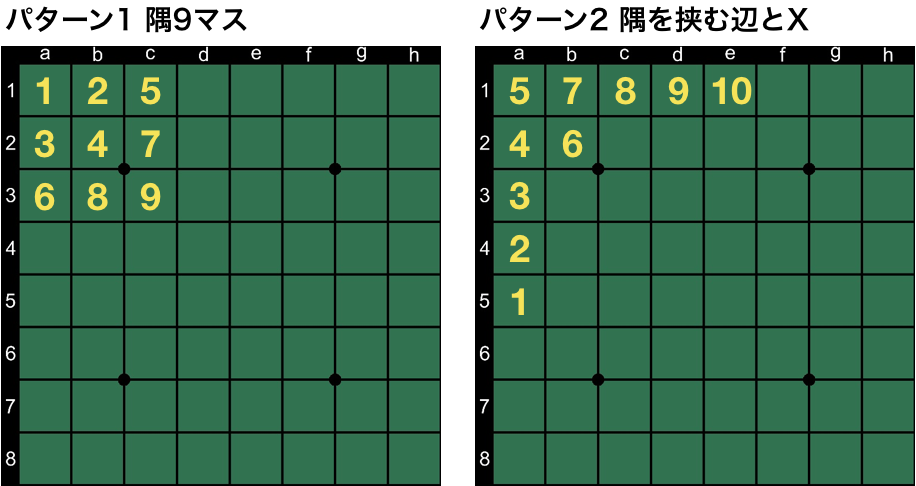
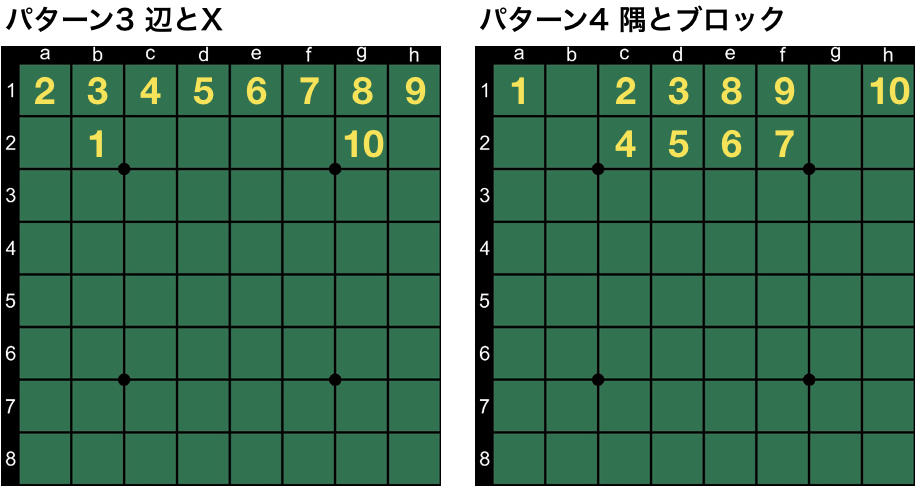
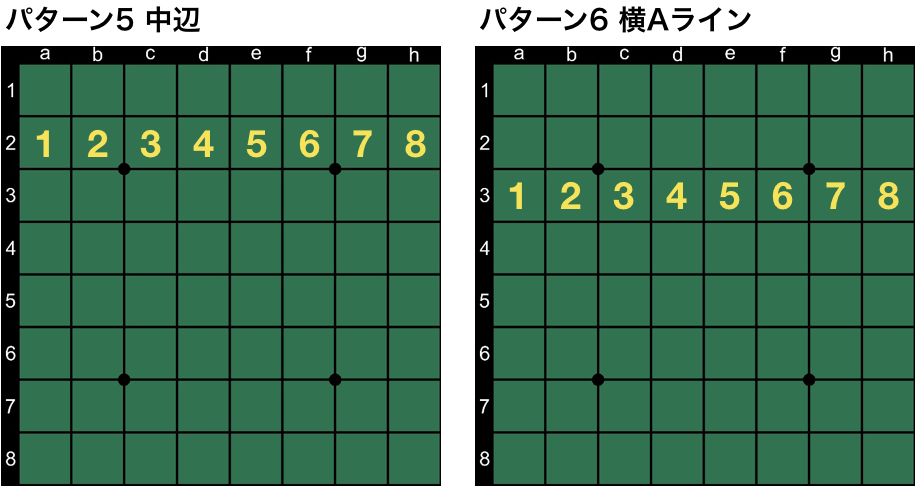
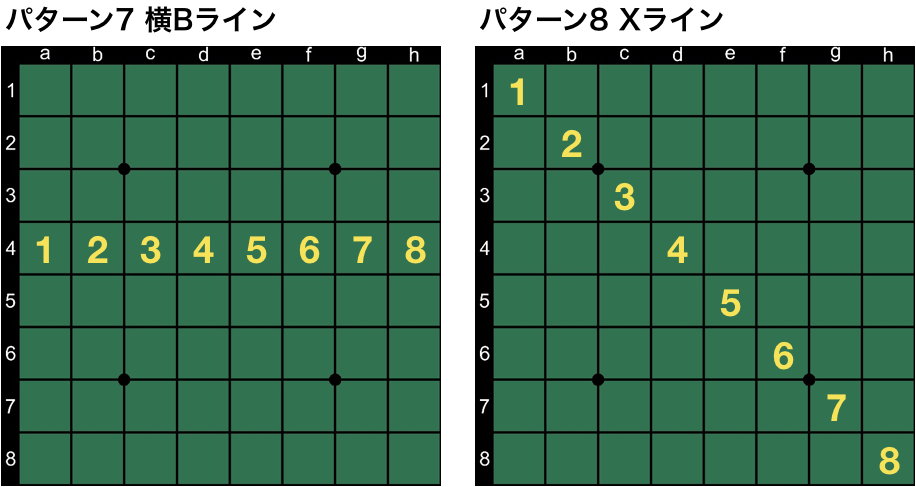
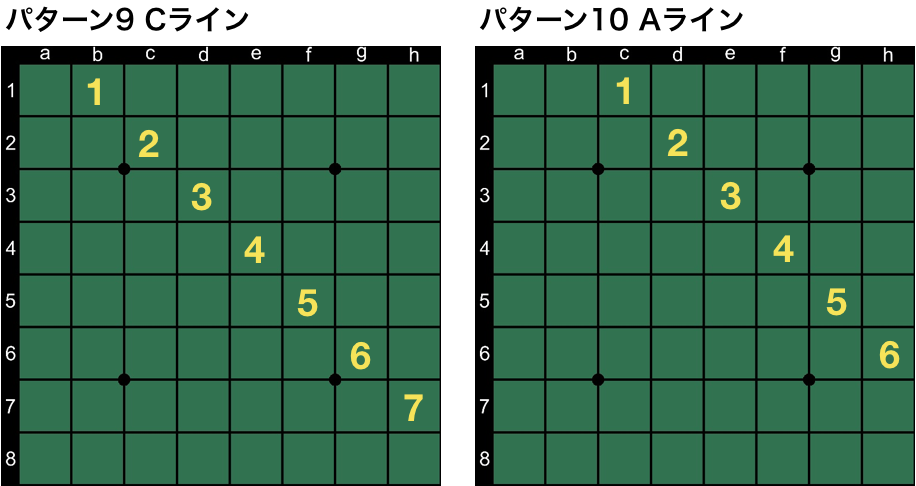
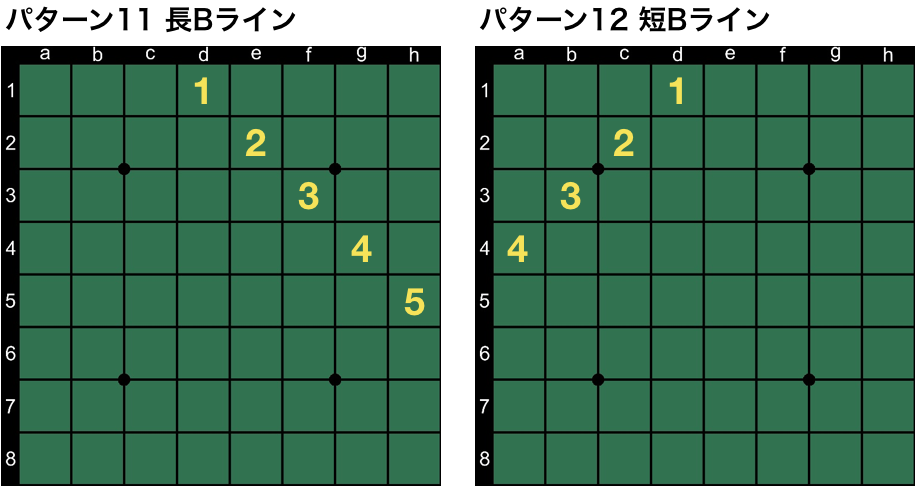
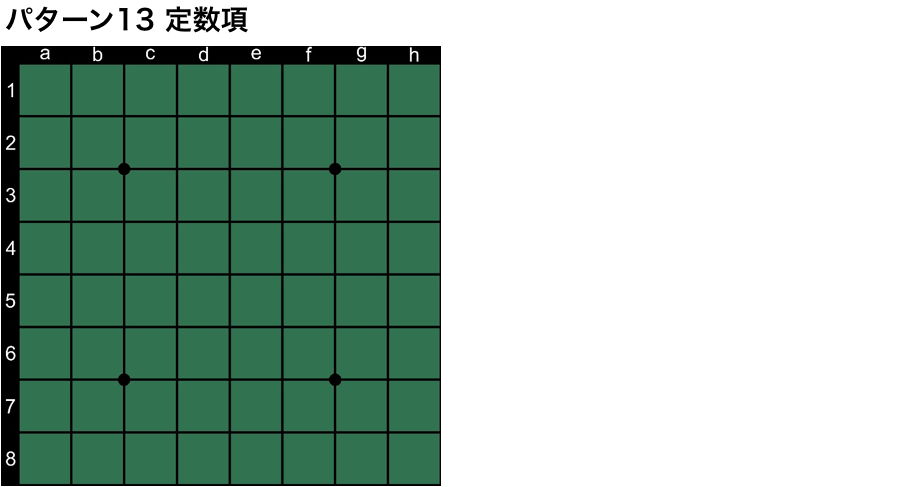
最後のパターン13は盤面の貼り付け誤りではありません。石の置かれ方に無関係な定数項的なスコアも何手目かの手番ごとに定義されています。あと、便宜上パターン6と7は横A/Bラインと名付けましたが、もちろん対象形には縦向きのものもあります。
| パターン | feature数 | マス数 | 配置数 | 配置数(対称除く) |
|---|---|---|---|---|
| 1. 隅9マス | 4 | 9 | 19683 | 10206 |
| 2. 隅を挟む辺とX | 4 | 10 | 59049 | 29889 |
| 3. 辺とX | 4 | 10 | 59049 | 29646 |
| 4. 隅とブロック | 4 | 10 | 59049 | 29646 |
| 5. 中辺 | 4 | 8 | 6561 | 3321 |
| 6. 横Aライン | 4 | 8 | 6561 | 3321 |
| 7. 横Bライン | 4 | 8 | 6561 | 3321 |
| 8. Xライン | 2 | 8 | 6561 | 3321 |
| 9. Cライン | 4 | 7 | 2187 | 1134 |
| 10. Aライン | 4 | 6 | 729 | 378 |
| 11. 長Bライン | 4 | 5 | 243 | 135 |
| 12. 短Bライン | 4 | 4 | 81 | 45 |
| 13. 定数項 | 1 | 0 | 1 | 1 |
さて、筆者の想像ではここを読んでいる方のほとんどは、これまでの長い長い文章は読み飛ばしてパターンの図と上記の表だけを見ている状況だと思うので、ここでEdaxの評価関数が何だったのかを簡単にまとめておきます。
- 上記13パターン47種類のfeatureそれぞれについて、可能性のあるすべての石の配置に対してスコアが与えられている
- スコアは手番(現局面が何手目か(0〜60))によって異なる値となっている
- これらのスコアは対称形をうまく省略して
eval.datに格納されている - 評価値は、局面に対してこれらの47個のfeatureのスコアを足して128で割った値
つまり、61通りの手番に対し、これらの10206+29889+...+1=114364個の値、つまり61*114364=6976204個の値を丸暗記すれば、あとは足し算と割り算だけでオセロの初心者でもEdaxの(静的)評価値を求めることができるのです!
ただ冒頭でも書いた通り、Edaxは探索を行って現局面から先の局面で評価関数を実行して、両者最善を尽くした場合の評価値を求めているので、実際には丸暗記だけでなく探索の能力も必要となることを付け加えておきます。
クリスマスプレゼント
ここまで読んでいただいた方に一足早いクリスマスプレゼントがあります。Edaxの静的評価関数を47個のfeatureに分解して表示するプログラムを作成しました。局面に対応してfeatureごとのスコアが表示されます。
簡単に使い方を書いておきます。
- まず最初にeval.datを読み込んでください。
- サーバから読み込むリンクをクリックすると、クラウドにおいてあるeval.datファイルを読み込みます。ただし十数MBの通信が発生することになりますので、読み込みには時間がかかります。通信量が気になる方は次のローカル読み込みをご利用ください。(二度目以降は状況によりキャッシュされている場合もあります)
- 端末内にeval.datファイルをお持ちの方は、「eval.dat(ローカルから)」でファイルを選択してください。
- あとは適当に手を進めてください。局面に対応したfeatureごとのスコアが表示されます。
- パスは自動では行われないので、ラジオボタンで黒番・白番を変更してください。
- チェックボックスをチェックすることで、手動で盤面や手数を好きなように設定することも可能です。
- 盤面の編集が可能なので、例えば序盤なのに隅9マスを黒が独占している、みたいな局面も作れてしまいますが、現実的にあり得ない状況に対するfeatureの値は適切でない可能性が高いです。
- なので、盤面を編集して部分的な形のfeatureの値を見たい場合は、手数を30以降くらいに手動設定して見た方が良いと思います。
- 表示されるのは全く先読みをしない評価関数の値(言い方を変えるとレベル0の評価値)です。当然精度が高いものではないので注意してください。
またソースコードについての注意点です。
- このプログラムはGPL v3ライセンスのオープンソースソフトウェアとします。
- オリジナルのEdaxはunpackして
EVAL_WEIGHTをメモリ上に展開していましたが、本プログラムはメモリ節約のため、packしたままメモリに保持しています。ソースを読まれる方はご注意ください。
もしオセロの初心者がEdaxの評価関数を読んだら
さて、ここでこの記事のタイトルに戻ります。もちろん某有名小説のタイトルのパロディですが、もし仮にオセロの初心者がこの評価関数だけを見てオセロを学んだらどういうことになるのかを、いくつか考えてみました。
隅は強いか
先ほどのViewerで、手動のチェックボックスを入れて、A1,A2,A3,B1,C1あたりに黒石を置いてみましょう。あれ?評価値がマイナスになりましたか?注意書きにも書きましたが、0手目のままだと適切な評価になりません。実際の0手目の状態で隅を取っていることはないですからね。手動で30手目くらいだということにしてみてください。評価値がプラスになりませんでしたか?
やはり隅付近を押さえているというのは強いと判断できるようです。ただ、評価値の内訳を見てみると、隅9マスとしてはあまり高くなく、辺に関わるものが高めに出ていると思います。隅は辺に展開していくことを見越して評価が高い、ということを評価関数から学ぶことができそうです。
打てる場所の数は大事か?
オセロの入門本には、試合の途中では石の数よりも打てる場所の数が大事だということが大体出てきますが、評価関数から学べるでしょうか?
まず気づくのは、評価関数は盤の一部の石の形だけを見て付けるスコアを47個足したもので、そもそも打てる場所の数というのを全く見ていないことになります。ただ、全てのラインの形は見ています。パターン5〜12はもちろん、それに含まれない辺のラインや、斜めの短いラインもパターン1や3に含まれています。なので、ラインで打てる場所があるかは一応は全て見ているとも言えます。ただし、2方向・3方向に返るマスがあっても、個々のfeatureとしてはそれぞれ評価してしまい、それを単純に足してしまいますから、打てる場所の数はあまり正確には評価に反映されないようです。
評価関数からは、打てる場所の数の重要性についてはあまりうまく学べないように思われます。
辺の良し悪し〜ピュアウィングは悪形か〜
オセロの入門本には辺の形の良し悪しについて書いてあります。今年(2019年)、オセロ界に大きな進展をもたらした『現代オセロの最新理論』では、辺の形に対して手数を単位にプラスマイナスの評価をしていました。
「辺の形」というとき、大体は辺の6マスと中辺の4マスを指すことが多いと思いますが、残念ながらこれらの範囲を包含するパターンは出てきませんでした。近いものとしてはパターン3の「辺とX」とパターン4の「隅とブロック」ですが、どちらも一部が欠けています。
『現代オセロの最新理論』によれば、例えば、悪い順にピュアウィング、ピュアブロック、ピュア山となっていますが、パターン4の「隅とブロック」ではこれらは区別がつきませんし、パターン3の「辺とX」では区別はつきますがピュアかどうかはわかりません。評価関数の算出方法は全てのパターンを独立して評価していて、パターン3が山でパターン4の中辺がピュアな場合、というような複合的な評価はしていません。あくまでもパターン3とパターン4のそれぞれの形だけをみて評価しているのです。これでうまくいくのでしょうか?
では、実際にViewerで、先ほどと同様に30手目くらいにしてピュアウィングを作ってみるとどうでしょうか。きちんとマイナス評価になっています。
ただ、内訳を見てみてください。辺に絡む評価はそれほど悪くなく、むしろ中辺に絡む評価が低くなっているかと思います。評価関数だけから学んだ初心者は、現状知られているような辺の形としての理解ではなく、例えばピュアウィングは中辺の形が悪いと理解することになりそうです。
逆偶数は悪いか
白番で自分から打てない奇数空き(いわゆる逆偶数)を作るのは悪形であるというのも、オセロを学ぶ上で大事なことです。典型的に逆偶数ができやすい隅付近や辺は、47個のfeatureの中のパターン1「隅9マス」やパターン4「隅とブロック」でカバーできて確かに低評価になっています。しかし、47個のfeatureだけでは判断できないような逆偶数については悪いことだと学ぶのは難しそうです。
おわりに
ここまで読まれた方の中には、Edaxの評価関数はこれで本当に大丈夫なのだろうか、という心配を持たれた方もいらっしゃるかもしれません。特に辺についての解釈は、筆者のオセロについての理解と異なるものだったので、最初はEdaxのプログラムの読み方か、Viewerの実装を間違えたのではないかと思いました。が、素のEdaxでBookを切ってレベル0で探索させた結果ときちんと一致するので、おそらく読み方や実装は合っていると思います。(もし間違いを見つけた方はご連絡いただけると助かります)
Edaxはご存知の通り人間ではまず勝てない強いプログラムです。上記の疑問についての、現時点での筆者の理解は以下の通りです。
- 終盤(20数マス空きくらいから)は終局までの完全読みをしていて、確実な評価になっている
- 中盤も探索を行った先で適用する評価関数なので、評価関数でカバーできない要素は探索という行為である程度カバーされている
- 序盤はさらに深い探索量を実現できるよう、Bookという仕組みが備わっている
- これらの条件下では、今回見てきた評価関数で十分な評価が得られる
むしろ、これまでのオセロに関する人間の理解の仕方(セオリー)が適切ではない可能性もあるかもしれません。Viewerを動かしてみることでオセロに関する新たな洞察が得られたら、筆者もこの記事を書いた甲斐があります。
やっと評価関数を探る長い長い旅も終わりを迎えました。この旅で見たものを信じるか信じないかは、あなた次第です。
