FUJITSU Advent Calendar 2017 part2 の21日目の記事です.
この記事の内容は個人の見解であり,所属する会社,組織を代表するものではありません.
ことわり
この記事では,計算論的学習理論という表現を,ある意味で記号処理的な(機械学習)システムとほぼ同意義で使います.パーセプトロンや確率・統計的手法が最近は主流ですが,(過去にはそうであったように)再び記号処理的な機械学習が脚光を浴びることがあるかもしれません.ただし,計算論的学習理論には,確率・統計的な要素が含まれる手法もあるため,やや偏った見方であることをご承知ください.
この記事を書いた背景
- 計算論的学習理論に関する記事が Qiita に全く無いので,1つくらいあってもいいのではないかと感じていたから
- せっかく記事を書くならば,アドベントカレンダーに参加してみたかった
- 私自身は,人工知能関連は全くの業務外で,クラウドインフラ関連の仕事をしている
- 業務外の内容なので,守秘義務(?)的なことに神経を尖らせなくて良さそうという利点はあった
- クラウド関連であれば,OpenStack,Ansible など内容が被りそうだし,既に多くの方が有意義な記事が Qiita にあるし,アドベントカレンダーは基本的にネタ被りNGとのことなので,思い切って業務に直結ではないエントリーにした
- 富士通でも人工知能,機械学習は今後の(も)重要なテーマであるはずだから
計算論的学習理論(Computational learning Theory)とは?
- 単に「学習理論」とも呼ばれる
-
計算理論に基づいた学習のモデルであり,具体例から概念学習をする
- 特に,(形式)言語に関する学習について言及されること多いように思う
- Wikipedia の機械学習の項目では,機械学習のアルゴリズムと分析についての理論的な側面というような紹介がされており(ja, enともにーというか,ja のほうは en の訳っぽい),理論計算機科学の1つと紹介されている1
- 人工知能・機械学習関連だけではなく,数学(再帰理論),哲学の方面からも関心を持たれている
- 個人的な印象では,とりわけ Algorithmic learning theory(以下ALT)で論じられる E.M.Gold による 極限による学習を指し計算論的学習理論と表することが多いと感じる(ので,その部分を特に解説する)
- 再帰理論の項目でも,学習理論を極限学習の理論と紐付けている
- ALTの歴史が長いという理由があるのかもしれない
- ALTの他に,PAC学習,EXACT学習,VC理論等がある 参考になるスライドがあったのでリンクさせていただく
形式言語理論について簡単に紹介
- 言葉を表層的な文字列としてとりあえず扱う理論
- 文字列の操作能力との関係で, Computer Science とも関連して発展してきた
- 文字列とかの定義は昔の記事に書いたのでみて(といっても標準的な定義だけど)
- 👆に加えて$\varepsilon$は空語とよばれる長さ0の文字を表す記号で, $\Sigma^{*} = \Sigma^+ \cup \{\varepsilon\}$ とする
- $L \subseteq \Sigma^{*}$なる$L$を言語という
- 空でない言語を少なくとも1つ含む言語の集まりを言語族という
- 言語の受理系として,オートマトンと呼ばれる抽象機械(状態機械)がある
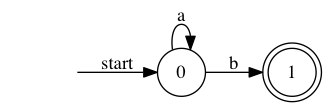
- 以下に示すのが,言語$L=\{ a^{n}b \ |\ n \in \mathbb{N}\} = \{b,ab,aab,aaab,...\}$ を受理するオートマトンである(コンピュータ感がある⚙)
start の状態から遷移をはじめ,◎の状態で終了すれば,その語を受理したことになる
- 以下に示すのが,言語$L=\{ a^{n}b \ |\ n \in \mathbb{N}\} = \{b,ab,aab,aaab,...\}$ を受理するオートマトンである(コンピュータ感がある⚙)
図1:言語$L=\{ a^{n}b \ |\ n \in \mathbb{N}\}$を受理する有限オートマトン
上記のように,記号による単純な推移だけで表現でき,メモリーや書き換えをもたない抽象機械を有限オートマトンとよび,有限オートマトンがで受理できる言語の全体を正規言語とよぶ.つまり,正規言語は,1つの言語族である.
例えば, $\{a^nb^n \ |\ n \in \mathbb{N}\}$などは,有限オートマトンで受理できない言語である.($n=3$のように具体的な自然数ならば,有限オートマトンで受理できるが)
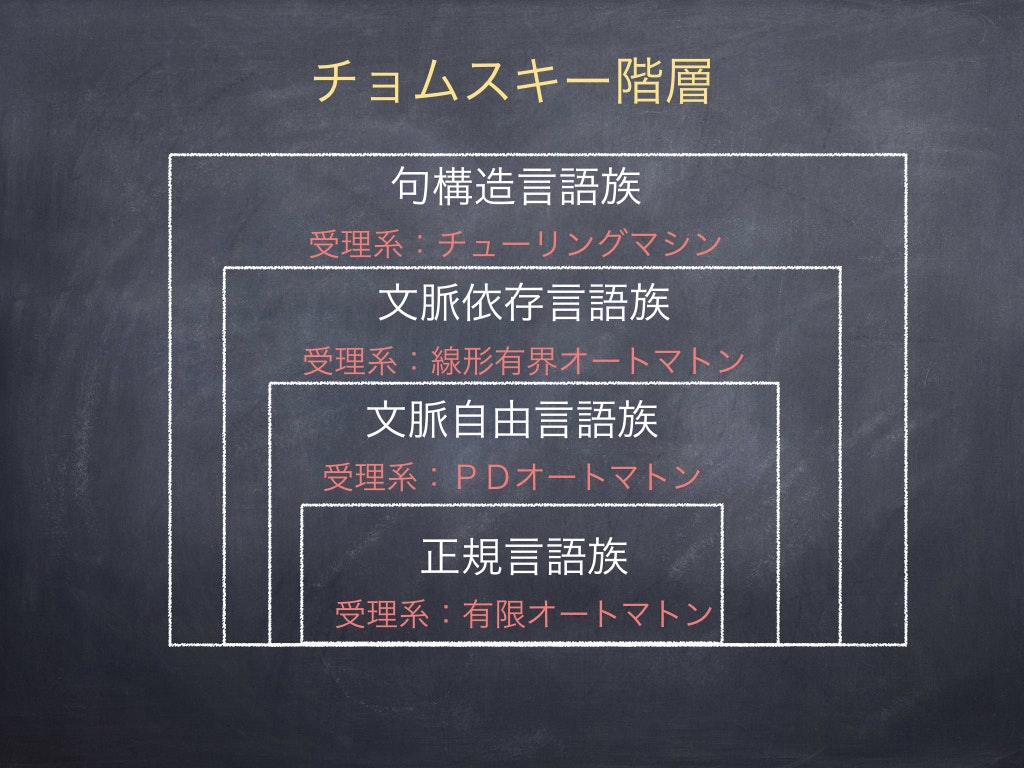
このように,言語という文字列の集合に対して,ある種の言語の複雑さが存在する.そして,その複雑さは,受理できる抽象機械の能力で真に階層化でき,階層ごとに言語の集合(言語族)が存在する.代表的な階層としては,チョムスキー階層と呼ばれるものがある.
ところで,$\Sigma = \{0,1\}$ に対して,以下の有限オートマトンは,$L = \{x_1 x_2 x_3 \ | \ x_1 + x_2 + x_3 ≧ 2\}$ となる言語を受理する.このように,言語は単に文字列の集合だとしても,その背景に関数的な関係のような表現もすることができる(そしてそのことから,文字列の受理が数学的な計算能力と密接に関わることも理解できると思う)
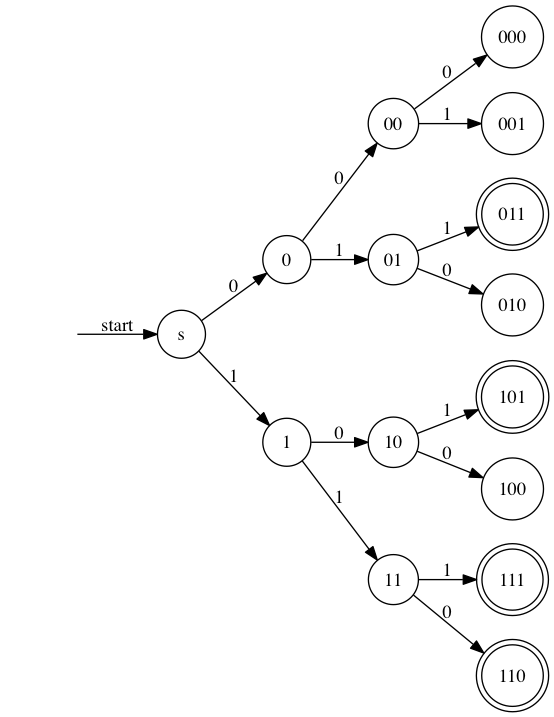
図3:$L = \{x_1 x_2 x_3 \ | \ x_1 + x_2 + x_3 ≧ 2\}$を受理する有限オートマトン
計算論的学習理論の詳細
上でも述べたように,計算論的学習理論では形式言語を対象とすることが多いので,以下では学習対象となる概念として言語を仮定する.
計算論的学習理論では,学習する全体集合であるところの学習領域,学習領域の部分集合であるところの概念,概念の族であるところの概念クラス,学習者の推測の表現であるところの仮説(これは概念に対応する),仮説全体である仮説空間がある.今回は,形式言語を対象とするため,以下のようになる.
- 学習領域:$\Sigma^{*}$
- 仮説空間(表現系の族) $\mathfrak{R}$:表現(今回で言えば,抽象機械)の族
- e.g $\mathfrak{R} = \Sigma$上で構成できるすべての有限オートマトン2
-
仮説(表現) $R \in \mathfrak{R}$
- e.g. 図1の有限オートマトン
-
概念クラス $\mathfrak{L}_\mathfrak{R}$:Rの各要素によって表される言語の族
- e.g $\mathfrak{L}_\mathfrak{R} = \{Gで受理できる言語\ |\ G \in \mathfrak{R}\}$
-
概念:言語$L$
- e.g. $L=\{ a^{n}b \ |\ n \in \mathbb{N}\}$
-
推論機械 $M$:具体例入力 → 計算 → 仮説出力 を無限に繰り返す TuringMachine
-
完全提示:$\Sigma^{*}$上の任意の語が一度は現れるような無限列で,かつ,各語に概念$L$の要素か否かのラベルも付与されたもの
-
正提示:完全提示の正のラベルだけのバージョン
-
計算論的学習理論では,ある推論機械$M$がある概念クラスの任意の概念を学習(同定)できるかを判定したい
-
何故ならば,特定の概念だけを学習する機械が存在することは(その概念が帰納的埋経可能である限り)自明である
-
ある概念クラスの任意の概念を学習できる機械が存在することが重要である
Algorithmic learning theory
- WikipediaのALT項目にもあるように統計的な機械学習と差異が謳われている
Algorithmic learning theory is different from statistical learning theory in that it does not make use of statistical assumptions and analysis.
- Gold によって提案された,極限による学習を扱う
- 比較的ノイズの少ないものが学習の対象
- (形式)言語や,科学的発見など,対象自体が数学的・形式的な要素を含む場合が多い
- このノイズの少なさという条件は,対象が数学的なものであることと密接に関連しているように思う
極限による学習(極限学習)
- 提示$s_1, s_2,...$に対して,推論機械$M$が推測する仮説$R_1,R_2,...$が$R$に収束するとは,$\exists k \ \mbox{ s.t. } \ n ≧ k → R_n = R$であることをいう
- $L$の任意の提示に対して,$M$の仮説がある$R$に収束し,$L$が$R$による言語であるとき,$M$が$L$を極限同定するとよぶ
- $M$が概念クラス$\mathfrak{L}_\mathfrak{R}$の任意の概念を極限同定するとき, $M$は$\mathfrak{L}_{\mathfrak{R}}$を極限同定するという
理論的な結果
正例からの学習不能性
以下の有名な理論的な結果は, Gold による
定理:超有限な言語族は正例のみから学習不能である
超有限な言語族とは, $\Sigma^*$上の全ての有限言語と少なくとも1つの無限言語を含むような言語族である.例えば,$\Sigma=\{a,b\}$とした場合,超有限な言語族は$\{\{\varepsilon\}, \{a\}, \{b\}, \{a,b\},..., \{a^n\},... \}$となる
証明(インフォーマルに...時間があればもっとフォーマルに直します):
はいりほうを用いる.もし,超有限な言語族を正例のみから極限学習可能だとすると,任意の言語の任意の正提示に対して,極限学習が可能ということである.しかし,よくよく考えてみると,この族は無限集合であり,ある言語に推測がFixした(ように思えた)後でも,その言語を包含するより大きな言語(の要素)が反例的に出される可能性は否めない.つまり,この後出しジャンケンが無限にできてしまうのである٩(๑`^´๑)۶
そのため,同定できないような提示が作れてしまうが,これは(任意の提示に対して同定できるということに)矛盾.$\square$
この Gold による結果は,正データから学習に関して,極めて否定的な印象を与えた.実際,正規言語は超有限な言語族でもあるため,この結果は,チョムスキー階層の最下層である,正規言語ですら正データから学習できないことを示したのである.実際,この後10年間は,正データからの学習に関して,目立った結果がなかったくらいである.
有限の厚み
次のような概念クラス(言語クラス)の概念(言語)は正提示から極限学習可能である
学習領域の任意の語に対して,その語を含むような言語が有限個であるような言語族
パターン言語による正データからの学習
有限の厚みは, パターン言語族 とよばれるものがもつ性質である.パターン言語族とは,チョムスキー階層による言語族とはまた異なる言語族であり,例えば以下のようなパターン言語からなる族である.
- $\Sigma = \{a,b\}$ 上のパターン$\pi = abx$に対して,パターン言語$L(\pi) = \{ aba, abb, abaa, abab,abbb,...\}$
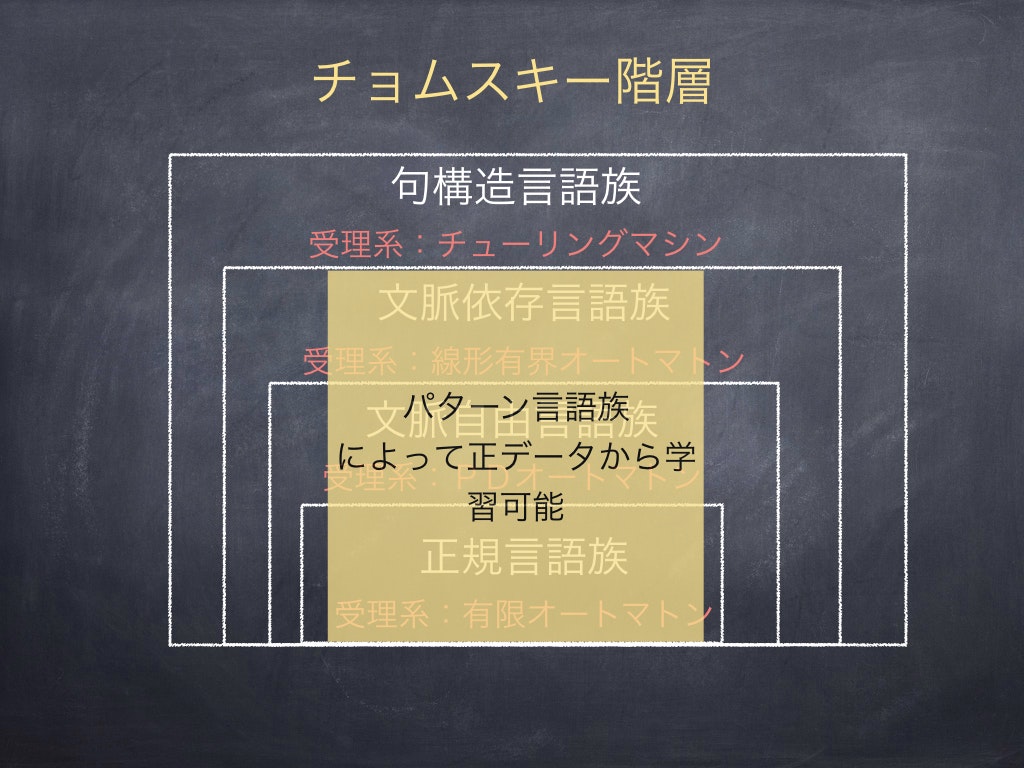
この言語族はかなり豊潤な表現力をもち,かつ,正データから学習できる[1].また,パターン言語族の和に関しても,正データからの学習可能性が証明されており,これらはチョムスキー階層の各層をすべて覆うことができないものの(先に示したアッパーバウンド),文脈依存言語までを横断的にかつかなりの精度まで近似することができる3
図4:パターン言語族による正データからの学習とチョムスキー階層のイメージ
パターン言語による正データからの学習は,遺伝子情報処理などにこの結果は応用されているようである.
その他の計算論的学習理論の理論
Exact学習
- 教師が存在し,現在の仮説の等価性質問(判例があれば教えてもらえる)が可能
- 同じように,仮説の要素に関して,所属正質問(Yes/No)を返してもらえる
PAC学習(Probably approximately correct learning)
- ある程度の例から,ある程度の正確さで,ある程度の時間内に学習をする理論
- 学習領域から確率分布に基づいて,ランダムサンプリングした具体例を提示する
帰納論理プログラミング(Inductive logic programming)
- 帰納推論や機械学習と論理プログラミングの境界にある
- 論理プログラミングはprologなどに代表されるが,ILPでは直接prologが用いられるわけではなく,その理論がベースにある論理体系であることが多い
- ILPとALTは関係が強く,ALTに関する結果は,ILPに関連する考察からも得られている
- 久木田水生氏(現 名古屋大学大学院情報科学研究科准教授)によると,以下の通り,ILPは,哲学・論理学における帰納推論においても興味深い対象であるようだ[2]
まず科学的方法に関して。ILP は科学史上、初めて実際的に成功した帰納論理の体系であり、この ILP の成功、とくに ILP を利用した機械学習システムによる科学的法則の発見は、科学哲学において支配的だった「機械的な帰納法は科学的方法ではない」という論調に対して明確な反例を突きつけるものである。というのも ILP システムは、完全に機械的な手続きに基づいて帰納的推論を行なうものであり、その意味では帰納的推論の規則を明示化した帰納論理の体系であると考えることができるからである。科学の歴史上初めて、帰納的推論の論理学が体系的に確立され、しかもそれが実際的な科学的成果を上げているという点で、これは画期的な出来事だと評価できる。
-
何故,学習が論理と関係するのか考えてみた
- 数学的対象というノイズの少ない(というよりは全くないといっていいかもしれない)対象を扱うと,真偽での判定がしやすくなる
- 論理的な考察というのは,この真偽的なな割り切りが往々にしておこなわれる(正確にはこれは古典論理等が対応し,真偽の2値でない論理の体系も多分にあるが)
- wikipedia にある ALT の以下の解説はとてもよくて,(適切な学習概念であれば)うまくきれいに既知の具体例を説明することを要求している
-
It is required of the learner that at each step the hypothesis must be correct for all the sentences so far.
-
つまり,論理学でいうところのモデルが存在するような規則を対象にするならば,上記の性質を満たしやすいのではないだろうか?
極限による学習は,学習なのか?
- いつ学習が完了したかわからない学習アルゴリズムは有効でないように思われるかもしれない
- しかし,よくよく考えると,我々が何かを学んだ際,十分な能力が身についたかを把握・意識することは少ない
- 例:日本語をいつ不自然なく使えるようになったかを覚えている人はあまりいない
- つまり,学習者が学習完了を意識しない状況というのは,そこまで荒唐無稽な話ではなく,むしろ,ある意味自然でもある
- 不完全性定理に関する著書や最近では情報学史やソフトウェア産業に関する啓蒙で有名な林晋教授が20060612のOCW講義動画でこのことに関する考察を,ヒルベルトの有限基底定理に絡めて述べられている^4
なぜ学習理論(記号処理的機械学習)を振り返ったの?
- 上でも述べたが,記号処理的な機械学習・人工知能が,再び脚光を浴びる可能性もある
- 東ロボくんの数学の部分もWatsonさんでも,記号処理ベースのエンジンが動いている
- 富士通ソリューションスクエアで開催されたマルレク(社内の参加者は多かったはず)でも,丸山不二夫氏が人工知能の歴史を振り返るの講演で,言語や数学といった初期人工知能の分野の重要性を主張されていた記憶があり,印象に残っていたので
まとめ
駆け足で説明したが,計算論的学習理論(特に,ALTのように)ノイズがないような単純な形式言語のモデルの学習においても,理論的にも哲学的にも興味深い結果をみることができた.これらについて,今後理論やハードに関するブレイクスルーがおこり,パーセプトロンなども絡めながら,新しい機械学習の可能性を見いだせたら嬉しい.
パターン言語族に関する話や帰納論理プログラミングに関してももっと詳細を述べたかったし,林晋先生の動画で言及されているような,極限学習と算術階層に関する話題も調査したかったが,今回は時間の関係で紹介することができなかった.これらについては,次回の課題としたい(あるいはこの記事を時間を見つけてエンハンスする).
最後に,私の愛読書である,高橋正子先生の「コンピュータと数学」の引用で終わりたい.
ある意味で時代に先んじて世に出た初期の研究が,折に触れて新しい風を受け次の世代に受け継がれていくことがあってもよいのではないかと思います.
参考文献
- [1]有川節夫(監修),西野哲朗,石坂裕毅,形式言語の理論 第2刷,丸善,1999:計算論的学習理論の定義に関することや,解説についてはこの本を大いに参考にした
- [2]久木田水生,帰納論理プログラミング,哲学論叢 (2006),33: 103-113
- [3]山本章博,帰納論理プログラミングの基礎理論とその展開,日本ソフトウェア科学会 2006
-
ニューラルネットワークやパーセプトロンにもアルゴリズム的議論があるはずだが,Wikipediaでは,学習理論だけで全ての機械学習アルゴリズムの分析についての理論とみなせるような書き方に読めて釈然としなさがある.また,多項式時間も,下で述べる極限学習の話では要請されない気もするのでこれも釈然としない ↩
-
本来ならば,仮説空間,および,仮説については,受理系のオートマトンではなく,文字列の生成系であるところの形式文法を仮定することが一般的なようだが,今回はわかりやすさを重視してオートマトンにした ↩
-
このように,理論的なアッパーバウンドが示された後に,その隙間を縫うような豊潤な結果が示されるということは,ロジックや計算論においてよくみられる結果に思う ↩