はじめに
こんにちは!カバー株式会社でインターンをしています。
本記事はカバー株式会社 Advent Calendar 2024の23日の記事です。
11月末にCGエンジニア検定エキスパートを受験したので、勉強がてら毎回第2問で出るアフィン変換をUnityで実装してみました。
Unity上で過去問の回答を再現できることを目標にしていきます。UnityのインスペクタからいじれるTransformコンポーネントを再現するようなことをやっていきます。Unityの回転は内部的にはQuaternionという数学が使われていますが、今回はそこまで立ち入りません。
アフィン変換とは
3DCGにおけるアフィン変換とは拡大・縮小・回転などの線形幾何学変換のことです。簡単に言うと、ある4次正方行列を乗じることで座標系を変換し、それぞれのボクセルを移動させることです。
3次正方行列では平行移動が表現できませんが、次元を上げて4次にすることで平行移動を含めた変換が実現できます。(これを同次座標系と呼びます。)その他の細かい話はネット上にたくさん記事があるのでそちらを参照ください。
今回は剪断(shear)については扱いません。
平行移動
平行移動は以下の行列で表現できます。
ここで、Aを変換前の4次元ベクトル、A'を変換後の4次元ベクトルとします。
A=
\begin{pmatrix}
x\\\
y\\\
z\\\
1
\end{pmatrix}
A' =
\left(
\begin{matrix}
1 & 0&0&tx\\\
0 & 1&0&ty\\\
0 & 0&1&tz\\\
0 & 0&0&1
\end{matrix}
\right)
A
どうしてこの行列になるかは実際に積計算をしてみるとわかるかと思います。
回転行列
回転行列が一番直感的でないですが、まずは定義を書きます。$\theta$は回転角度です。
x軸周りの回転
A' =
\left(
\begin{matrix}
1 & 0&0&0\\\
0 & \cos(\theta)&-\sin(\theta)&0\\\
0 & \sin(\theta)&\cos(\theta)&0\\\
0 & 0&0&1
\end{matrix}
\right)
A
y軸周りの回転
A' =
\left(
\begin{matrix}
\cos(\theta) & 0&\sin(\theta)&0\\\
0 & 1&0&0\\\
-\sin(\theta) & 0&\cos(\theta)&0\\\
0 & 0&0&1
\end{matrix}
\right)
A
z軸周りの回転
A' =
\left(
\begin{matrix}
\cos(\theta) & -\sin(\theta)&0&0\\\
\sin(\theta) & \cos(\theta)&0&0\\\
0 & 0&1&0\\\
0 & 0&0&1
\end{matrix}
\right)
A
証明はネット上に数多くあるためご自身で調べてください。
簡単な覚え方があるので紹介します。
- (4,4)成分に1を埋め、4行4列の他の要素を0埋めする
- x軸周りなら(1,1)成分に1を、yなら(2,2)に、zなら(3,3)に1を書く
- その1と同じ行と列を0で埋める
- 残った部分を行列式が1になるように$\sin$,$\cos$で埋める
- $\theta=0$を代入して表現行列が単位行列になることでも検算できる
- y軸周りの$\sin$の符号にだけ注意
拡大縮小
拡大縮小は以下の行列で表現できます。
A' =
\left(
\begin{matrix}
sx & 0&0&0\\\
0 & sy&0&0\\\
0 & 0&sz&0\\\
0 & 0&0&1
\end{matrix}
\right)
A
こちらも展開してみるとわかりやすいですね。
Unityにおける実装
先の式をUnityに実装していきましょう!
今回検証のためにUnity2022.3.22f1を使用しましたが、特定バージョン依存の実装はしていないので他のバージョンでも使えます。
アフィン変換のためのメソッド
UnityにはMatrix4×4という回転や移動のためのメソッドが提供されています。Matrix4×4は4次正方行列を扱える、まさにアフィン変換のための構造体です。
メソッドを利用して簡単に移動先の座標を求めることもできますが、今回は行列の各要素に数値を直接入れてプリミティブに座標を求めていきます。
Matrix4×4の各要素には[0]~[15]の一次元配列でアクセスできます。Unityでは列オーダー(Matrices in Unity are column major)であるため、左上から下に向かってアクセスしていきます。(shaderは行オーダー)
実装
回転と平行移動のメソッドの実装を一気に紹介します(拡大縮小は略)。
//平行移動
Matrix4x4 SetTransformMat(float tx, float ty, float tz)
{
Matrix4x4 mat = Matrix4x4.identity;
mat[0] = 1;
mat[1] = 0;
mat[2] = 0;
mat[3] = 0;
mat[4] = 0;
mat[5] = 1;
mat[6] = 0;
mat[7] = 0;
mat[8] = 0;
mat[9] = 0;
mat[10] = 1;
mat[11] = 0;
mat[12] = tx;
mat[13] = ty;
mat[14] = tz;
mat[15] = 1;
return mat;
}
//X軸周りの回転
Matrix4x4 SetRotateXMat(float rx)
{
Matrix4x4 mat = Matrix4x4.identity;
float rad = rx * Mathf.Deg2Rad;//ラジアン角に変換
mat[0] = 1;
mat[1] = 0;
mat[2] = 0;
mat[3] = 0;
mat[4] = 0;
mat[5] = Mathf.Cos(rad);
mat[6] = Mathf.Sin(rad);
mat[7] = 0;
mat[8] = 0;
mat[9] = -Mathf.Sin(rad);
mat[10] = Mathf.Cos(rad);
mat[11] = 0;
mat[12] = 0;
mat[13] = 0;
mat[14] = 0;
mat[15] = 1;
return mat;
}
//Y軸周りの回転
Matrix4x4 SetRotateYMat(float ry)
{
Matrix4x4 mat = Matrix4x4.identity;
float rad = ry * Mathf.Deg2Rad;//ラジアン角に変換
mat[0] = Mathf.Cos(rad);
mat[1] = 0;
mat[2] =- Mathf.Sin(rad);
mat[3] = 0;
mat[4] = 0;
mat[5] = 1;
mat[6] = 0;
mat[7] = 0;
mat[8] = Mathf.Sin(rad);
mat[9] = 0;
mat[10] = Mathf.Cos(rad);
mat[11] = 0;
mat[12] = 0;
mat[13] = 0;
mat[14] = 0;
mat[15] = 1;
return mat;
}
//Z軸周りの回転
Matrix4x4 SetRotateZMat(float rz)
{
Matrix4x4 mat = Matrix4x4.identity;
float rad = rz * Mathf.Deg2Rad;//ラジアン角に変換
mat[0] = Mathf.Cos(rad);
mat[1] = Mathf.Sin(rad);
mat[2] = 0;
mat[3] = 0;
mat[4] = -Mathf.Sin(rad);
mat[5] = Mathf.Cos(rad);
mat[6] = 0;
mat[7] = 0;
mat[8] = 0;
mat[9] = 0;
mat[10] = 1;
mat[11] = 0;
mat[12] = 0;
mat[13] = 0;
mat[14] = 0;
mat[15] = 1;
return mat;
}
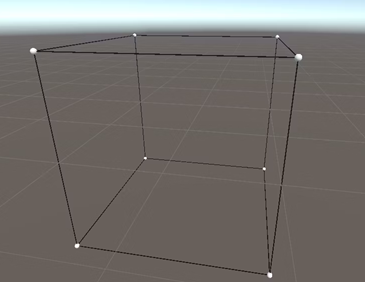
キューブの頂点を模したSphereの辺をLine Rendererで補間しキューブを表現しました。
普通にプリミティブ図形のCubeを使用しなかったのは、直接キューブの頂点にアクセスして動的にメッシュを生成するのがめんどうだったからです。
本当はアフィン変換適用後に埋められなかったボクセルの補間などが必要なのですが、今回はLine Rendererを利用して補間しています。
先ほど定義したメソッドをUpdate内で呼び出すことでキューブの移動が実現できます。
verticesがキューブの各頂点のゲームオブジェクトの配列です。
スペースを押すたびにオブジェクトが移動するようにしています。現在の頂点座標に右からアフィン変換行列を乗じることで移動先の座標が算出できます。
//z軸周りに10度ずつ回転する
if (Input.GetKeyDown(KeyCode.Space))
{
for (int i = 0; i < vertices.Length; i++)
{
vertices[i].transform.position = SetRotateZMat(10).MultiplyPoint(vertices[i].transform.position);//Z軸周りに10度回転
}
}
if (Input.GetKeyDown(KeyCode.Space))
{
for (int i = 0; i < vertices.Length; i++)
{
vertices[i].transform.position = SetRotateZMat(10).MultiplyPoint(vertices[i].transform.position);//Z軸周りに10度回転
vertices[i].transform.position = SetTransformMat(0,0.2f,0).MultiplyPoint(vertices[i].transform.position);//y軸方向に0.2移動
vertices[i].transform.position = SetScaleMat(0.9f,1, 1.05f).MultiplyPoint(vertices[i].transform.position);//x軸を0.9倍、z軸を1.05倍拡大
}
}
CGエンジニア検定エキスパートの過去問を解いてみる
せっかくなので、2024年後期の第2問を今回つくったスクリプトを利用して解いてみます。
問題では右手系なのに対して、Unityは左手系なのに注意です。
球同士の相対位置は合わせていますが、大きさやワールド座標を厳密には問題文と合わせていないため、問題文と少し位置が異なることをご容赦ください。
4つ球を配置し、それぞれの球に先ほどのスクリプトをアタッチしました。
a.
Z軸周りに-90度回転した後、X軸周りに180度回転する問題です。
gameObject.transform.position=SetRotateZMat(-90).MultiplyPoint(gameObject.transform.position);
gameObject.transform.position = SetRotateXMat(180).MultiplyPoint(gameObject.transform.position);
見事解答群のイと一致しました!(画像右側は試験問題63pから引用)
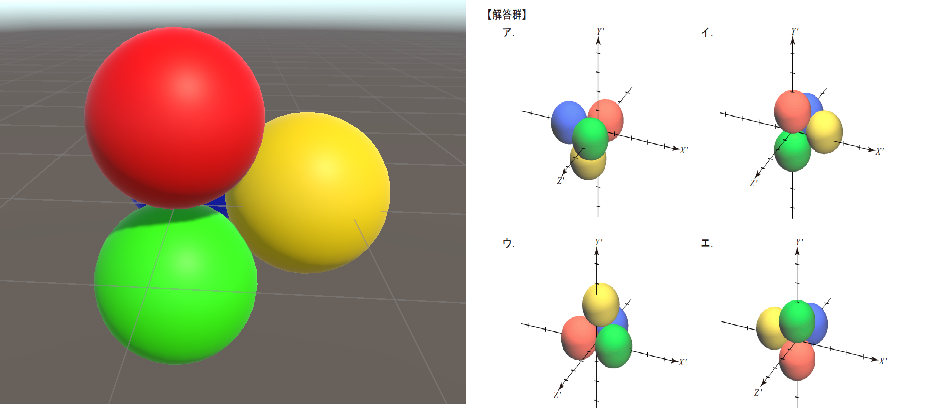
b.
わかりやすいように簡単に座標軸を追加しました。
座標系の違いを考慮して、Y軸回転とZ軸の移動を逆にすることが必要です。
これに注意してイの選択肢通りにしてみると、求めたい位置姿勢が得られました。
gameObject.transform.position= SetRotateYMat(90).MultiplyPoint(gameObject.transform.position);
gameObject.transform.position = SetRotateZMat(180).MultiplyPoint(gameObject.transform.position);//逆回転に注意
gameObject.transform.position = SetTransformMat(0,0,-1).MultiplyPoint(gameObject.transform.position);//逆移動に注意
c.
お次は計算問題です。
必ず操作順に右から順に行列を置いてください。
今回でいうと求めたい表現行列A'は以下のように表されます。
A' =
\left(
\begin{matrix}
1 & 0&0&0\\\
0 & \cos(-90°)&-\sin(-90°)&0\\\
0 & \sin(-90°)&\cos(-90°)&0\\\
0 & 0&0&1
\end{matrix}
\right)
\left(
\begin{matrix}
1 & 0&0&0\\\
0 & 1&0&1\\\
0 & 0&1&0\\\
0 & 0&0&1
\end{matrix}
\right)
A
以上をUnityで実装すると、
Matrix4x4 mat= Matrix4x4.identity;
mat = SetRotateXMat(-90)*SetTransformMat(0,1,0);
Debug.Log(mat);
アと一致しました!
余談ですが、一つずつ表現行列を現在のオブジェクトの三次元座標に乗じても、アフィン変換行列をすべて計算してからオブジェクトの三次元行列に乗じても同じ結果になります。
興味がある人は両方計算してみて結果を比べてみてください。
事前にアフィン変換行列を計算しておくことで一回の積計算で済み、計算が高速化できます。
d.
(4,4)成分以外の第4列が0でないならば平行移動です。
そうでなければ、回転移動です。
どの軸周りかは対角成分の1の位置を見ることでわかります。
後は角度を逆算するとエがx軸に1移動して、Y軸周りに180°回転するアフィン変換であることがわかります。
これを実装してみると、問題文と一致しました。

さいごに
最後まで読んでいただきありがとうございました!
特に回転行列の式が覚えづらかったですが、一度コツをつかめば再現しやすいです。時間があればVRChatなどのソーシャルVRプラットフォームで対話的に実装したいです。
CGエンジニア関連で次に実装してみたいのは内積計算をもちいた隠面消去やレイマーチングです。
明日の記事の担当はsugarさんです。




