今回は、Kuramoto-Sivashinsky方程式(蔵本シバシンスキー方程式と表記)について紹介したいと思います。
蔵本シバシンスキー方程式自体、英語の文献が多い印象があり、勉強する際にやや苦労しました。そういった背景があり日本語の記事があったほうが助かるなぁーと思い、今回記事にしようと思いました。
蔵本シバシンスキー方程式は以下の偏微分方程式で表されます。
\displaystyle \frac{\partial u}{\partial t}+ \frac{1}{2}\frac{\partial u^{2}}{\partial x}+ \frac{\partial^{2} u}{\partial x^{2}}+ \frac{\partial^{4} u}{\partial x^{4}}=0 \cdots(1) \\
u(x,t) = u(x+L,t), u(x,0)=g(x) \cdots(2)
式(2)は,周期条件と呼ばれるものです。$t=0$の時なので、$g(x)$は初期値関数です。
式(2)に含まれている$L$の値が小さい時は周期的な解が得られますが、$L$の値が大きくなると解が複雑化していきます(カオスともいう)[1]。
$L=2\pi$未満の時は解が0に収束することがわかっています[1]。
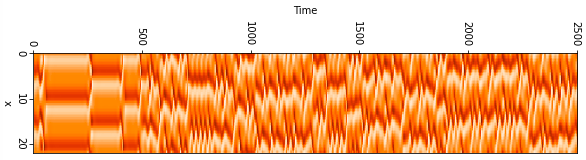
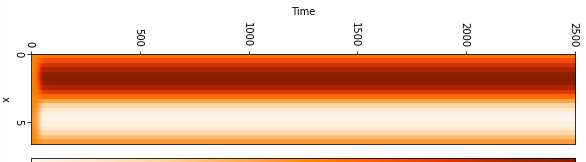
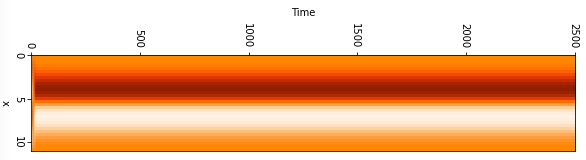
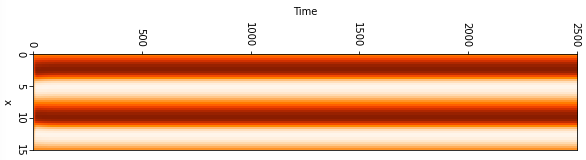
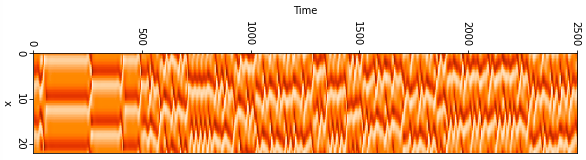
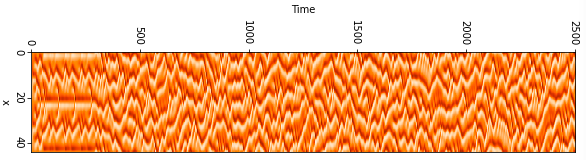
以下には$L=22$の場合の解を示している。横軸は時間t、縦軸は領域xを表している。
u(x,t)の値を色で表している。解が複雑化していることがわかる。
$L=\pi,1.9\pi,2\pi,2.1\pi,11,15,22,44$の場合の図を一番下に記載してあります。もし良ければご覧ください。$L=2\pi$未満の時は解が0に収束することがわかっており[1]、図からも確認できる。
参考・引用文献
[1] M.A. Bucci, O.Semeraro, A.Allauzen, G.Wisniewski, L.Cordier, and L.Mathelin, Control of chaotic systems by deep reinforcement learning
以下$L=\pi,1.9\pi,2\pi,2.1\pi,11,15,22,44$の場合の図になります。
