地図の作成
前回
ROS2環境上でのGazeboシミュレーションによってTurtlebot3の操作をrclpyを用いて行いました。
今回
今回は /scan と /odom からデータを取り出し、matplotlibにデータを出力します。
そして、次回はデータから最短距離を取り出し、そこから角度を割り出すことでぶつかるのを防ぐようにします。
アルゴリズム
- /scan と /odom からそれぞれデータを取り出します。
- データを整形します。
- 座標上にプロットするため、ベクトルをx成分・y成分に分解します。
- データをプロットします。
0. ロボットの動き
class Controle(Node):
def __init__(self):
super().__init__("turtlebot3")
self.pub = self.create_publisher(Twist, "/cmd_vel")
self.twist = Twist()
while True:
self.run(0.25, 0.0)
sleep(15)
self.run(0.0, 0.0)
sleep(5)
self.run(-0.25, 0.0)
sleep(15)
self.run(0.0, 0.0)
sleep(5)
def run(self, l, a):
self.twist.linear.x = float(l)
self.twist.angular.z = float(a)
self.pub.publish(self.twist)
今回用意したテスト用のロボット操作プログラムです。
前と後ろに移動するように速度を送っています。
1. /scan と /odom からデータを取り出す
以下はデータを取得するクラスです。
特にこれと言って難しい部分はありませんし、特徴的な部分はありません。
class make_map(Node):
def __init__(self):
super(make_map, self).__init__("turtlebot3")
# 型の初期化
self.position = Point()
self.orientation = Quaternion()
self.range = array(0)
self.angle = array(0)
self.range_max = array(0)
self.x = float(0.0)
self.y = float(0.0)
self.min_range = float(0)
self.min_angle = float(0)
# 読み込みノード作成
self.create_subscription(LaserScan, "/scan", self.LaserScan_callback)
self.create_subscription(Odometry, "/odom", self.Odometry_callback)
def LaserScan_callback(self, data):
self.angle_increment = data.angle_increment
self.angle = arange(90*self.angle_increment, 450*self.angle_increment, self.angle_increment, dtype=float32)
self.range = array(data.ranges)
self.range_max = float(data.range_max)
self.PositionCalc()
def Odometry_callback(self, data):
self.position.x = -data.pose.pose.position.y
self.position.y = data.pose.pose.position.x
self.orientation = data.pose.pose.orientation
2. データを整形
得られたデータは
/odom - クオータニオン
となっています。
ここで重要なのは計算をする上ではクオータニオンは計算はしやすい。
しかし、numpyの三角関数はRadian角を利用している。
そのため、 クオータニオン角からオイラー角に変換する必要があります。
変換には以下のプロセスで変換をします。
- クオータニオン -> 回転行列
- 回転行列 -> オイラー
では計算式を簡略に示します。
条件として、得られたデータの型を以下の形式とします。
Quaternion(x, y, z, w)
この形式をもとに行列を表現すると
\begin{matrix}
1-2y^2-2z^2 & 2xy+2wz & 2xz-2wy & 0\\
2xy-2wz & 1-2x^2-2z^2 & 2yz+2wx & 0\\
2xz+2wy & 2yz-2wx & 1-2x^2-2y^2 & 0\\
0 & 0 & 0 & 1\\
\end{matrix}
になります。上記では既に回転行列に変換されています。
更にこれをもとにオイラーフォーマットに変換をかけます。
変換には逆三角関数を利用します。
\begin{matrix}
\theta_x & = & sin^{-1}(2yz-2wx)\\
\theta_y & = & tan^{-1}(-\frac{2xz+2wy}{1-2x^2-2y^2})\\
\theta_z & = & tan^{-1}(-\frac{2xy+2wz}{1-2x^2-2z^2})
\end{matrix}
以上でオイラー角に変換ができます。数式をプログラムに書き換えます。
以下はクオータニオン角から回転行列への変換プログラムです。
def Quaternion2Matrix(ary: Quaternion) -> array:
x, y, z, w = ary.x, ary.y, ary.z, ary.w
m00 = 1 - 2*y**2 - 2*z**2
m01 = 2*x*y + 2*w*z
m02 = 2*x*z - 2*w*y
m03 = 0
m10 = 2*x*y - 2*w*z
m11 = 1 - 2*x**2 - 2*z**2
m12 = 2*y*z + 2*w*x
m13 = 0
m20 = 2*x*z + 2*w*y
m21 = 2*y*z - 2*w*x
m22 = 1 - 2*x**2 - 2*y**2
m23 = 0
m30 = 0
m31 = 0
m32 = 0
m33 = 1
return array([
[m00, m01, m02, m03],
[m10, m11, m12, m13],
[m20, m21, m22, m23],
[m30, m31, m32, m33]
])
そして回転行列からオイラー角に変換をかけるプログラムは
def Matrix2Euler(ary: array) -> array:
euler = Euler()
euler.x = arcsin(ary[2][1])
euler.y = arctan2(-ary[2][0], ary[2][2])
euler.z = arctan2(-ary[0][1], ary[1][1])
if ary[2][1] == 1:
euler.x = pi/2
euler.y = 0
euler.z = arctan2(ary[1][0], ary[0][0])
elif ary[2][1] == -1:
euler.x = -pi/2
euler.y = 0
euler.z = arctan(ary[1][0], ary[0][0])
return euler
ここで注意してもらいたいのは
Euler()
です。これは独自実装ですので一応classを以下に示しておきます。
class Euler():
def __init__(self):
self.x = 0.0
self.y = 0.0
self.z = 0.0
以上から変換をかけるプログラムはかけました。
また、変換の詳しい説明はこちらを参考にしてください。
とてもわかり易いので熟読することをおすすめします。
3.座標上にプロットするため、ベクトルをx成分・y成分に分解します。
これは単純にsinとcosを用いて分解するだけです。
self.x = self.range*cos(self.angle - euler.z) + self.position.x
self.y = self.range*sin(self.angle - euler.z) + self.position.y
上記のプログラムはPositionCalc関数内に書かれているものです。
これでによりプロットが可能となります。
4. データをプロット
matplotlibを用いてデータをプロットしましょう。
結果はこのようになりました。
かなりいい感じではないでしょうか?
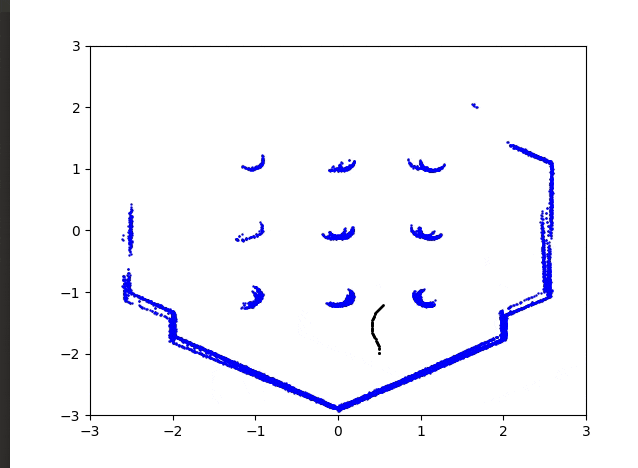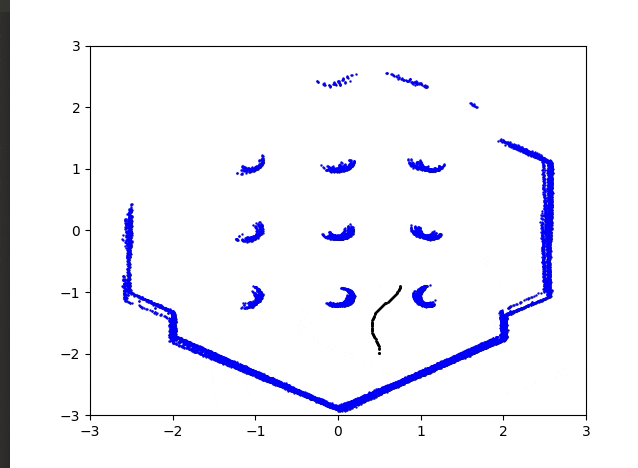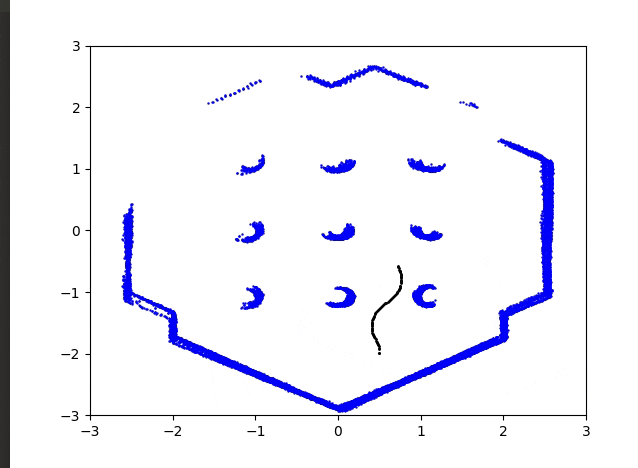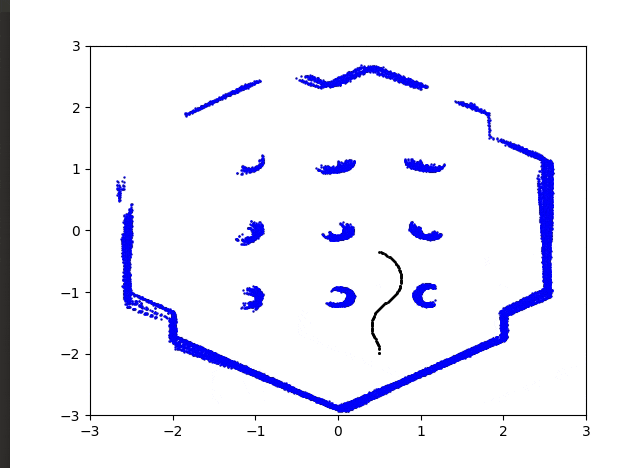
今後は点群マッチングなどを行い精度のいいマップをプロットできればいいと思っています。
修正したい箇所
プロットをOpen3Dに任せたい点。
次回
衝突回避