多腕バンディット問題

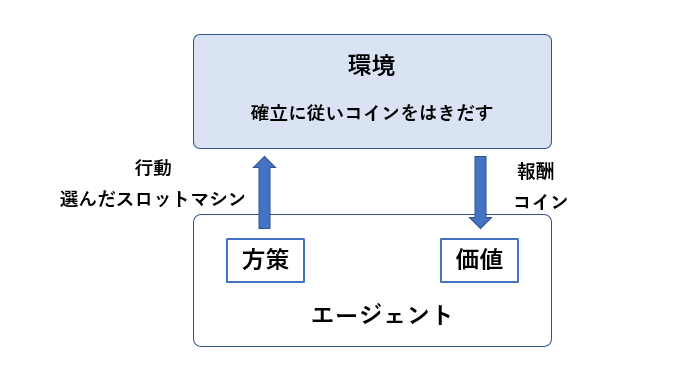
多腕バンディット問題(Multi-Armed Bandit Problem)とは

強化学習に含まれるもので、複数の選択肢の中らから報酬の高い選択肢を選ぶという問題です。例えば、コインの出る確率が異なる複数の「スロットマシン」で、決められた金額の中で一番あたりを出すためにはどれを選択すれば良いかということで考えることができます。

では、スロットで有名なジャグラーで多腕バンディット問題を見てみよう。
ex.) アイムジャグラーEX(6号機)

設定	BIG	REG	合算
1	1/273.1	1/439.8	1/168.5
2	1/269.7	1/399.6	1/161.0
3	1/269.7	1/331.0	1/148.6
4	1/259.0	1/315.1	1/142.2
5	1/259.0	1/255.0	1/128.5
6	1/255.0	1/255.0	1/127.5

※今回の制約として、20円スロットで50,000円を投入し、はき出されたメダルは一切使わず、50,000円で貸し出された50,000/1,000×50=2,500枚のみを使用する(1Play=3枚, 2,500/3 = 833回転)。また、スロットマシンは6台存在し、1つずつ1～6の設定がふられており、設定の重複はないものとする。

それでは検証をしていく。コインをいっぱいだしたいので高設定の台に座りたいが、使用するスロットマシンの設定はあらかじめ分からないため、初めのうちはランダムに座り、情報収集をする　→　 探索
そして、探索をもとに設定の高いと思われる台を選択する。　→　利用

探索と利用にはバランスが必要だが、そのバランスをとる手法としては『ε-greedy』と『UCB1』がよく使用されている。

ε-greedy

最適な行動を効率よく学習するための手法で、確率ε(0 ~ 1の定数)でランダムに行動を選択する。
学習初期はQ値に基づかず、ランダムで幅広く確認を行う。
※εは0.1が最適であることが多いみたい

※パッケージのインポートは以降の処理にも必要ですが、ここでしか記載しない。

import numpy as np
import random
import math
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline

class E_Greedy():
    def __init__(self, epsilon):
        self.epsilon = epsilon
  
    # 試行回数と価値のリセット
    def initialize(self, n_slots):
        self.n = np.zeros(n_slots) # 各台の試行回数
        self.v = np.zeros(n_slots) # 各台の価値

    # 台の選択
    def select_slot(self):
        if self.epsilon > random.random():
            # ランダムに台に座る
            return np.random.randint(0, len(self.v))
        else:
            # 価値が高い台に座る
            return np.argmax(self.v)

    # パラメータの更新
    def update(self, selected_slot, reward, t):
        self.n[selected_slot] += 1
        n = self.n[selected_slot]
        v = self.v[selected_slot]
        self.v[selected_slot] = ((n-1) / float(n)) * v + (1 / float(n)) * reward

    # 文字列
    def label(self):
        return 'ε-greedy('+str(self.epsilon)+')'

UCB1

Upper Confidence Bound 1の略で、試行の「成功率 + バイアス」を最大化にするための行動を選択する手法である。

UCB1 = \frac{w}{n} + \Bigr(\frac{2\log (t)}{n} \Bigr)

class UCB1():
    # 試行回数と価値のリセット
    def initialize(self, n_slots):
        self.n = np.zeros(n_slots) # 各スロットの試行回数
        self.w = np.zeros(n_slots) # 各スロットの成功回数
        self.v = np.zeros(n_slots) # 各スロットの価値

    # スロットの選択
    def select_slot(self):
        # nがすべて1以上になるようにスロットを選択
        for i in range(len(self.n)):
            if self.n[i] == 0:
                return i
        # 価値が高いスロットを選択
        return np.argmax(self.v)

    # パラメータの更新
    def update(self, selected_slot, reward, t):
        self.n[selected_slot] += 1    

        # 成功したとき成功回数に加算
        if reward == 1.0:
            self.w[selected_slot] += 1
        
        # 試行回数が0のスロットの存在時は価値を更新しない
        for i in range(len(self.n)):
            if self.n[i] == 0:
                return

        # 各スロットの価値の更新
        for i in range(len(self.v)):
            self.v[i] = self.w[i] / self.n[i] + (2 + math.log(t) / self.n[i]) ** 0.5

    # 文字列
    def label(self):
        return 'ucb1'

class Slot():
    def __init__(self, p):
        self.p = p # BIGかREGが当たる確率

    # 1Playごとの報酬
    def draw(self):
        if self.p > random.random():
            return 1.0
        else:
            return 0.0

シミュレーション

↑の『ε-greedy』と『UCB1』を用いて、シミュレーションを実行する処理を書いていく。
まず、スロットのクラスを。

class Slot():
  def __init__(self, p):
    self.p = p # BIGかREGが当たる確率

  # 1Playごとの報酬
  def draw(self):
    if self.p > random.random():
      return 1.0
    else:
      return 0.0

次に、シミュレーション関数を。

def play(algorithm, slots, num_sims, num_time):
    # 履歴の準備
    times = np.zeros(num_sims * num_time) # 何回目か
    rewards = np.zeros(num_sims * num_time) # 報酬

    for sim in range(num_sims):
        algorithm.initialize(len(slots))
        
        for time in range(num_time):
            index = sim * num_time + time
            # 履歴の計算
            times[index] = time+1
            selected_slot = algorithm.select_slot()
            reward = slots[selected_slot].draw()
            rewards[index] = reward
            # アルゴリズムのパラメータ更新
            algorithm.update(selected_slot, reward, time+1)

    # [ゲーム回数の何回目か, 報酬]
    return [times, rewards]

では準備が整ったのでスロットマシンの確立のセットと、実際にシミュレーションを実行する。

# スロット
slots = (Slot(1/168.5), Slot(1/161.0), Slot(1/148.6), Slot(1/142.2), Slot(1/128.5), Slot(1/127.5))

# アルゴリズム
algorithms = (E_Greedy(0.1), UCB1())

for algorithm in algorithms:
    # シミュレーションの実行(833回転させるのを1000回シミュレーションしてみる)
    results = play(algorithm, slots, 1000, 833)

    # グラフの準備
    df = pd.DataFrame({'times': results[0], 'rewards': results[1]})
    mean = df['rewards'].groupby(df['times']).mean()
    plt.plot(mean, label=algorithm.label())

# グラフの表示
plt.xlabel('Step')
plt.ylabel('Average Reward')
plt.legend(loc='best')
plt.show()

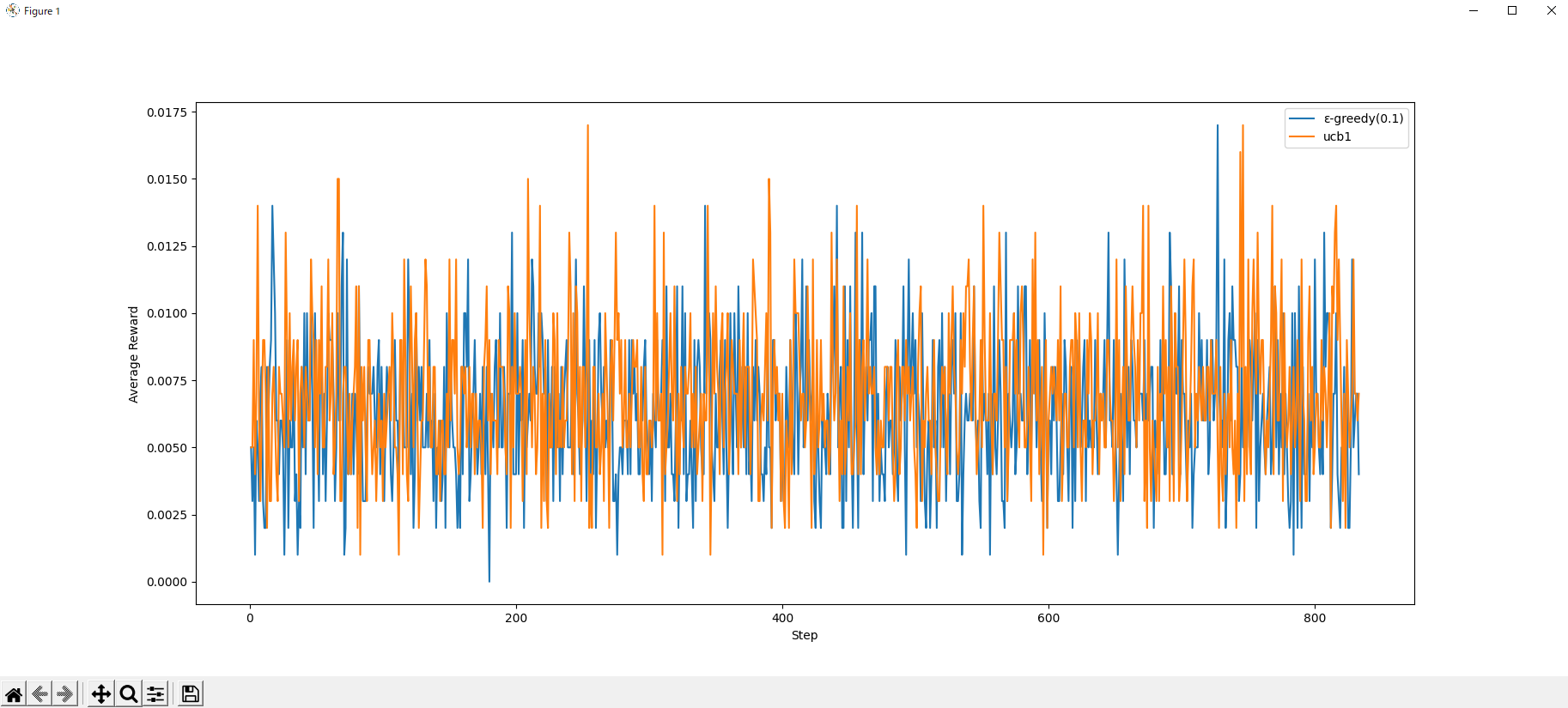
実行結果

結果、周期性は見られるものの、あんまり予測精度は高くなさそう...

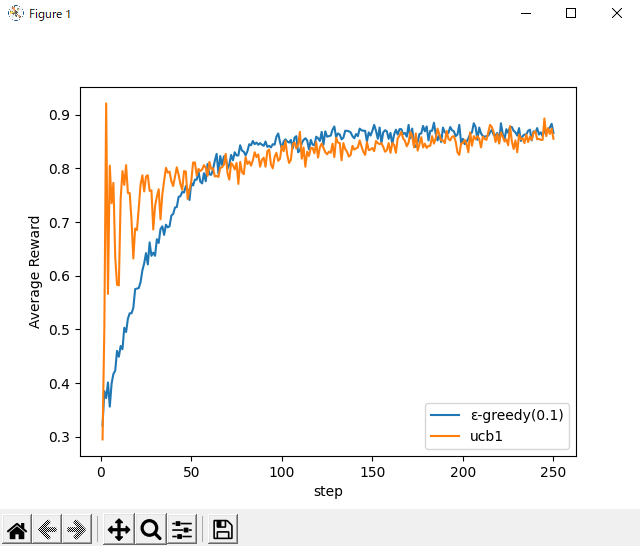
ちなみに有名なスロットアームの問題で使用される、確率0.3、0.5、0.9の問題だときれいなグラフで、開始当初は「UCB1」の方が報酬が高いという結果が見てとれる。

やはりスロットは、長年の勘や自分で台見てやった方がいいのかな...と思いました。